平滑滤波策略的应用

由来

我们在做峰值检测相关的工作，例如检测通用事件边界时，会经常出现明明检测出来某一帧属于边界的概率是峰值，但是模型却没有把该帧作为边界的情况，下面我们来解释出现这样情况的其中一种原因。

原因

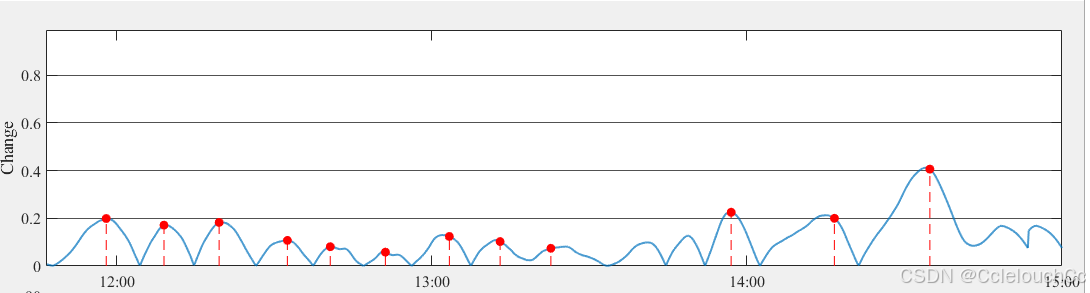
以上图为例，能明显看到在14：00之前有些帧明明属于峰值但是却没有将它标红（视为边界）。以往模型经过训练测试后会输出一个逐帧的均方误差文档，里面记载了每一帧的均方误差大小，平常我们只需要对其进行梯度计算，然后找局部最大值（峰值）即可。

但不同的是在进行梯度计算前模型还用了一个平均滑动，即每一帧的均方误差已经被平滑成了均值，例如现在有[0.5 , 1.2 , 2.5 , 3.6]，设置窗口为3，平滑原理为[(0.5+1.2+2.5)/ 3, (1.2+2.5+3.6)/3 , (2.5+3.6)/2 , 3.6]，最后两个窗口不够的就缩小窗口尺寸，例如第三个值2.5就只取2.5和3.6。进行了这样的平滑移动之后，其实每一帧的均方误差就已经改变了，但是在画图时我们用的坐标其实还是原始的均方误差，因此就会产生有些结果不在峰值上但也是边界，有些帧的梯度是峰值但是却不是边界。

移动平均滤波

举个例子来说明：
假设我们有一个数据序列：[1.5, 2.3, 1.8, 3.1]，窗口大小为3。

在正常情况下，平滑会使用窗口大小为3的窗口来计算每个数据点的平均值，如下：

第一个数据点：使用 [1.5, 2.3, 1.8]，计算 (1.5 + 2.3 + 1.8) / 3 = 1.87
第二个数据点：使用 [2.3, 1.8, 3.1]，计算 (2.3 + 1.8 + 3.1) / 3 = 2.4
第三个数据点：使用 [1.8, 3.1]（因为后面没有更多数据了），计算 (1.8 + 3.1) / 2 = 2.45
对于数据 3.1：平均值就只能取 3.1 本身。

该滤波目的是通过将一组相邻的误差值取平均来减少数据的噪声，使误差数据更平滑，能够更好地捕捉到长时间的趋势变化。