数学建模笔记（6）主成分分析

背景

例如，某人要做一件上衣要测量很多尺寸，如身长、袖长、胸围、腰围、肩宽、肩厚等十几项指标，但某服装厂要生产一批新型服装绝不可能把尺寸的型号分得过多?
我们可以把多种指标中综合成几个少数的综合指标，做为分类的型号，将十几项指标综合成3项指标，一项是反映长度的指标，一项是反映胖瘦的指标，一项是反映特殊体型的指标。因此，将众多因素融合为几个因素的这种方法叫做主成分分析法。

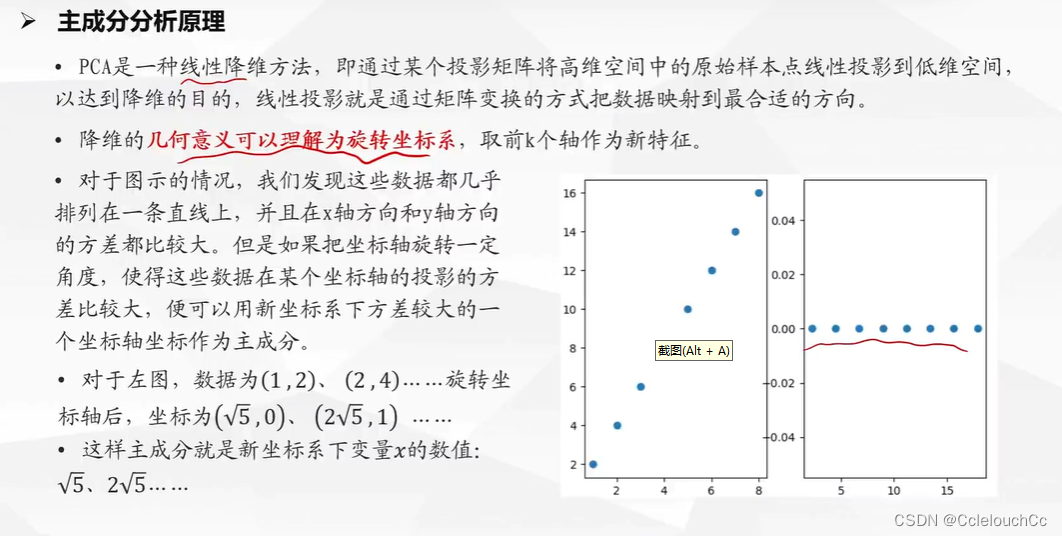
分析法原理

步骤

相关系数矩阵是一个与协方差矩阵密切相关的概念，用于衡量多个随机变量之间的线性关系强度和方向。与协方差矩阵不同的是，相关系数矩阵将协方差标准化。用这个矩阵的目的是找到第一个方差最大值（第一主成分）后，要保证第二主成分和第一主成分无关，这样才是不同的指标，因此就需要用到协方差矩阵/相关系数矩阵，来衡量成分的相关性。