层次分析法
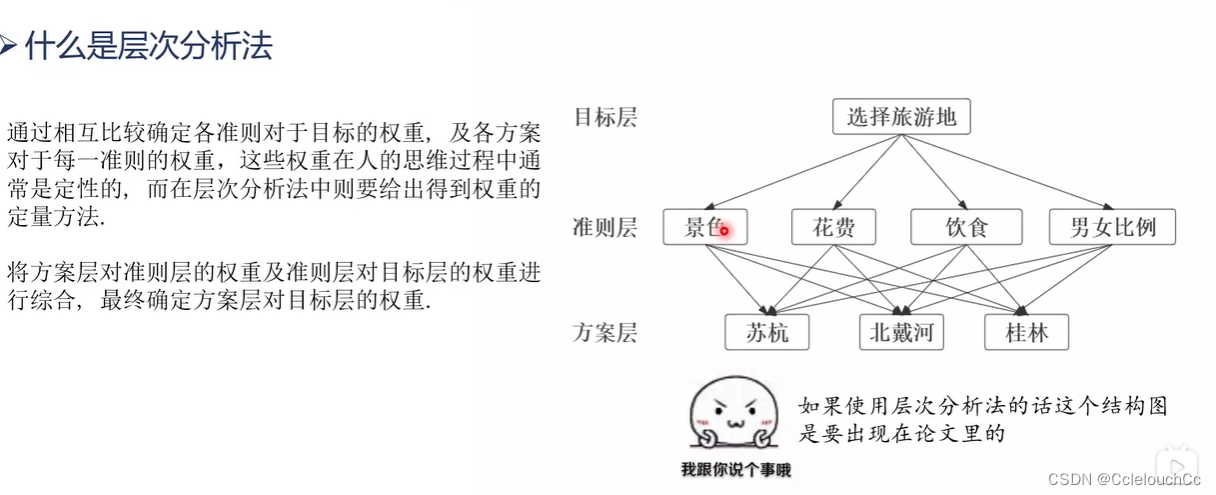
层次分析法的使用目的是为了解决各种评价性问题,例如,城市生态环境质量检测评价,旅游地选择评价等,具体步骤如下:

例子
1.提出问题


对该问题有以下几点,首先,四个条件的权重不同,可能景色条件大于价格条件,因此对四个条件应设置不同权重的占比,其次,再比较相同条件下各城市的分数,即哪个城市风景分数高,哪个城市分数低,并将这些分数进行归一化。
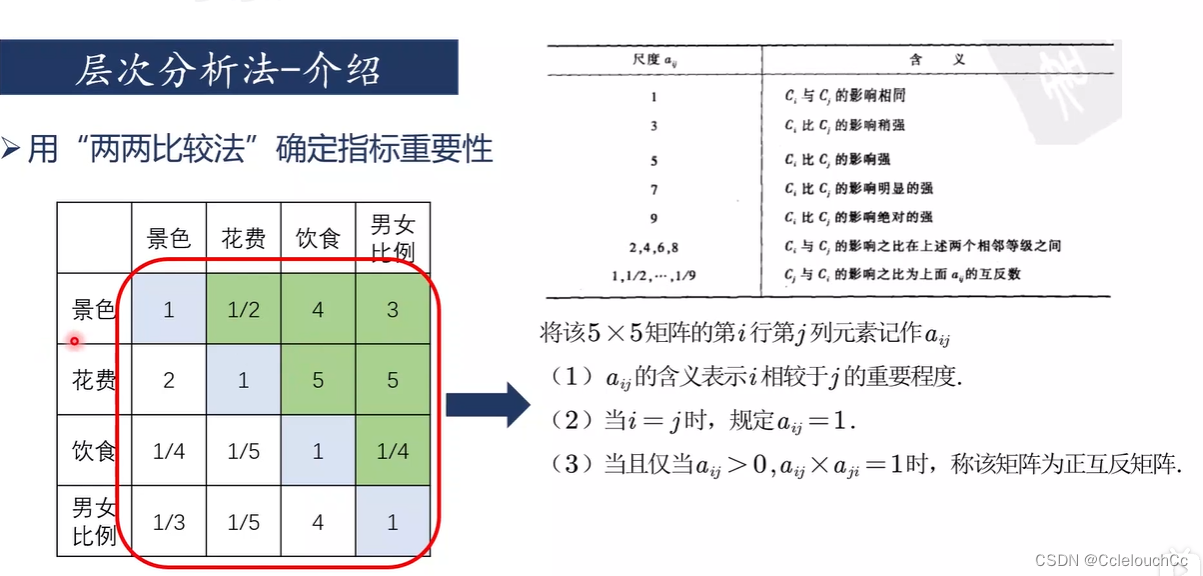
2.条件权重
首先,确定好四个条件之间的权重大小,该矩阵俗称为判断矩阵。例如,景色与花费相比,景色:花费=1:2,花费占两级重要,那么景色相对只有一级。可通过这样的判断矩阵进行计算从而得到权重向量,即知道四个条件的权重大小。
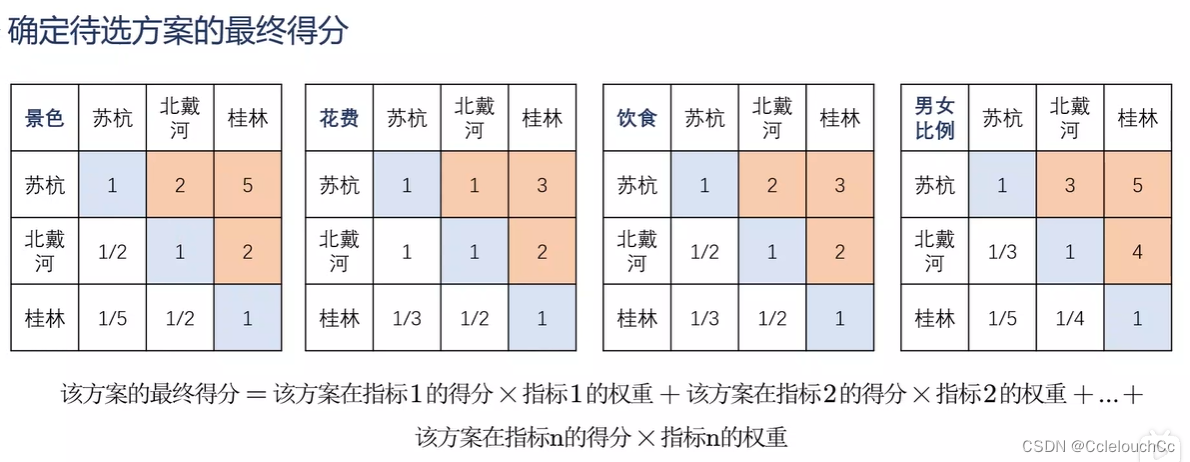
3.条件分数
将三地的四个条件分别进行对比,就会得到四个分数矩阵,以第一个景色为例,北戴河与苏杭之比=2:1,即北戴河的风景为二级,苏杭相较北戴河为一级。之后将得分的矩阵进行归一化,再乘以相对应的条件权重从而得到最后得分,哪个地方得分高则去哪个。
4.一致性检验
一致矩阵是用来检验矩阵矛盾的问题,所以在使用判断矩阵时要先检验其一致性。
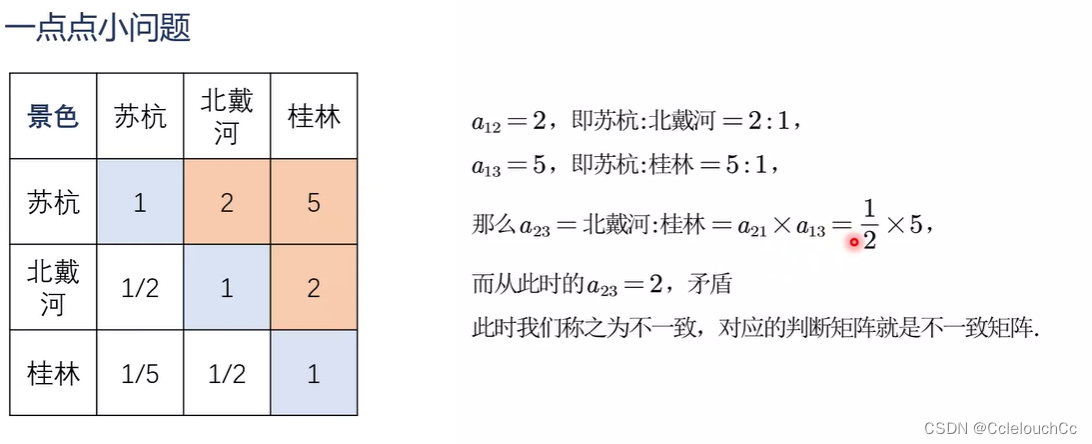
检验方法如下:


5.通过矩阵求权重
1.如果矩阵是一致性矩阵(每两行与每两列之间成倍数关系):直接将每一列的结果进行归一化,例子如下:可知该矩阵是一致矩阵,则
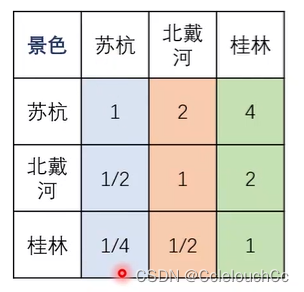
2.如果矩阵是非一致矩阵,则


6.结果
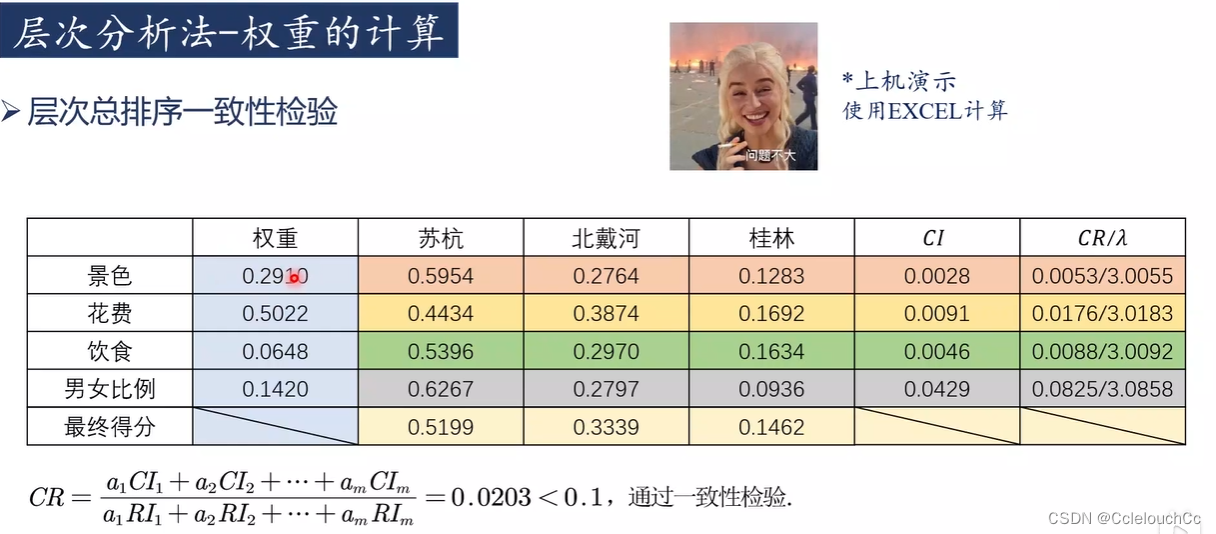




 本文介绍了层次分析法在解决评价性问题中的应用,如城市生态环境质量和旅游地选择。涉及步骤包括提出问题、确定条件权重、计算条件分数、一致性检验以及权重求解。通过实例说明了如何通过判断矩阵和归一化进行决策制定。
本文介绍了层次分析法在解决评价性问题中的应用,如城市生态环境质量和旅游地选择。涉及步骤包括提出问题、确定条件权重、计算条件分数、一致性检验以及权重求解。通过实例说明了如何通过判断矩阵和归一化进行决策制定。
















 3214
3214










