包含min函数的栈、栈的压入弹出序列、从上往下打印二叉树、二叉搜索树的后序遍历序列

1、包含min函数的栈

本题考点： 栈的规则性设计 牛客链接

题目描述：
定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的 min 函数，输入操作时保证 pop、top 和 min 函数操作时，栈中一定有元素。

此栈包含的方法有：
push(value):将value压入栈中
pop():弹出栈顶元素
top():获取栈顶元素
min():获取栈中最小元素

数据范围：操作数量满足0≤n≤300 ，输入的元素满足∣val∣≤10000
进阶：栈的各个操作的时间复杂度是O(1) ，空间复杂度是O(n)

解题思路：

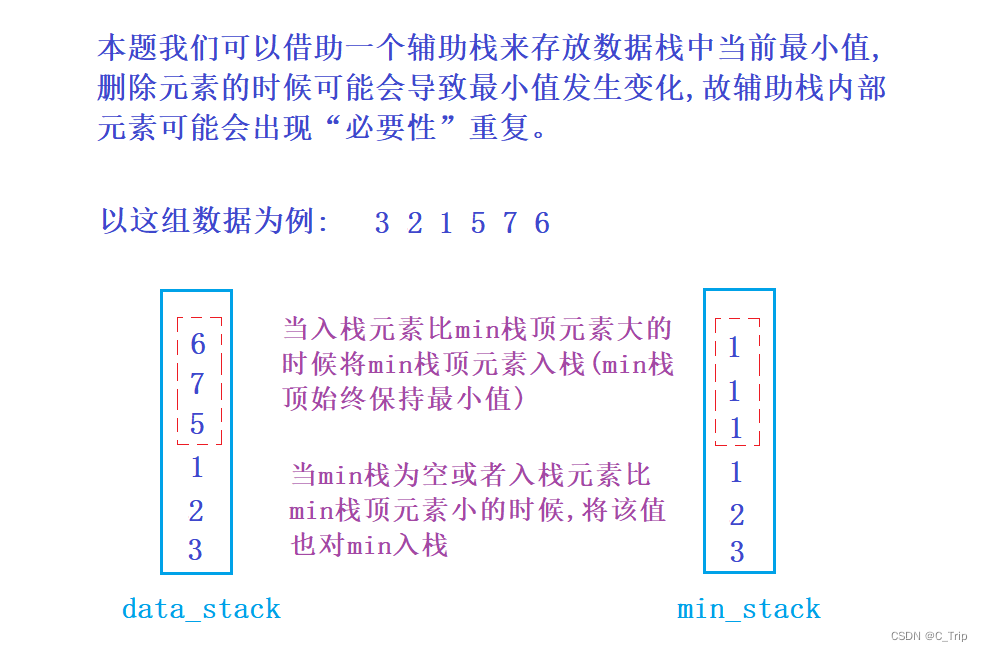
代码：

class Solution {
private:
    stack<int> data_stack;
    stack<int> min_stack;
public:
    void push(int value) {
        data_stack.push(value);
        if(min_stack.empty() || value < min_stack.top())
        {
            min_stack.push(value);
        }
        else // !min_stack.empty() && value >= min_stack.top()
        {
            min_stack.push(min_stack.top());
        }
    }
    void pop() {
        data_stack.pop();
        min_stack.pop();
    }
    int top() {
        return data_stack.top();
    }
    int min() {
        return min_stack.top();
    }
};

2、栈的压入弹出序列

本题考点： 栈的理解 牛客链接

题目描述：
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

1. 0<=pushV.length == popV.length <=1000
2. -1000<=pushV[i]<=1000
3. pushV 的所有数字均不相同

解题思路：

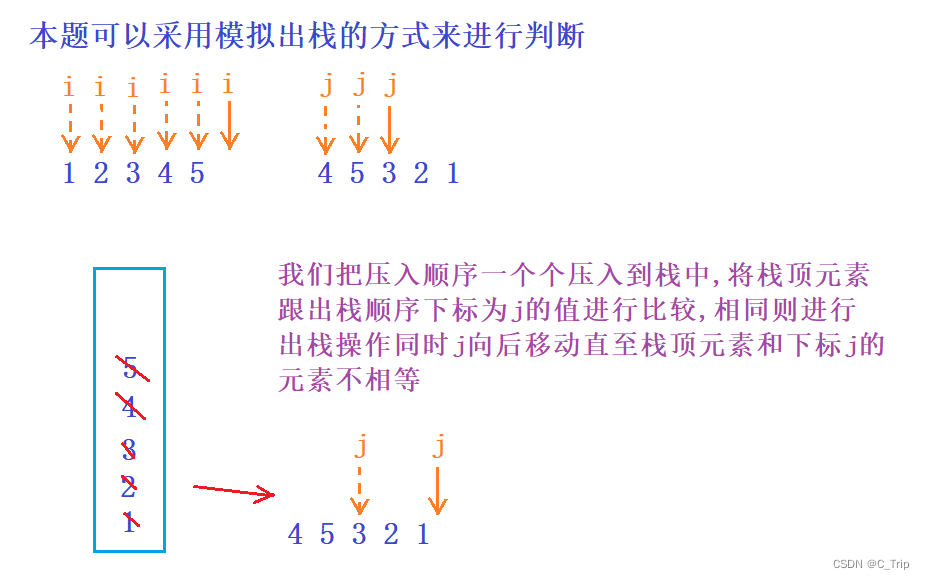
代码：

class Solution {
public:
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        
        int pushi= 0, popj = 0;
        stack<int> st;
        while(pushi < pushV.size()) 
        {
            st.push(pushV[pushi++]);
            while(!st.empty() && st.top() == popV[popj])
            {
                st.pop();
                popj++;
            }  
        }
        return st.empty();
        //return pushi == pushV.size();
    }
};

3、从上往下打印二叉树

本题考点： 二叉树层序遍历 牛客链接

题目描述：
不分行从上往下打印出二叉树的每个节点，同层节点从左至右打印。例如输入{8,6,10,#,#,2,1}，如以下图中的示例二叉树，则依次打印8,6,10,2,1(空节点不打印，跳过)，请你将打印的结果存放到一个数组里面，返回。
数据范围:
0<=节点总数<=1000
-1000<=节点值<=1000

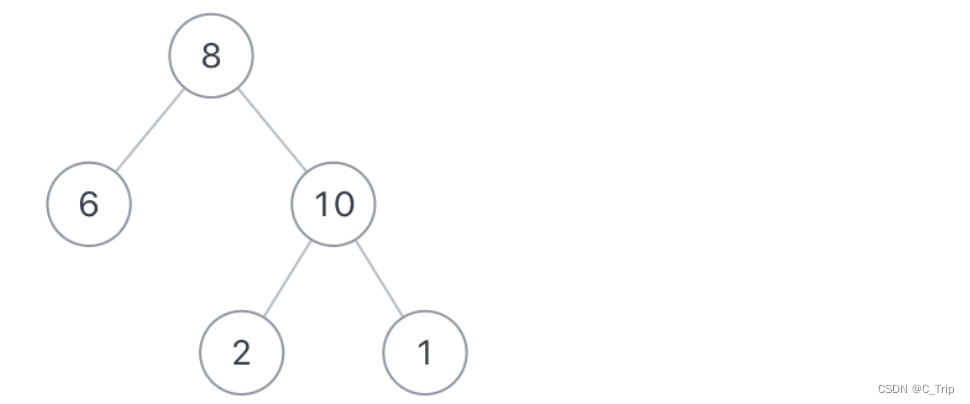
解题思路：

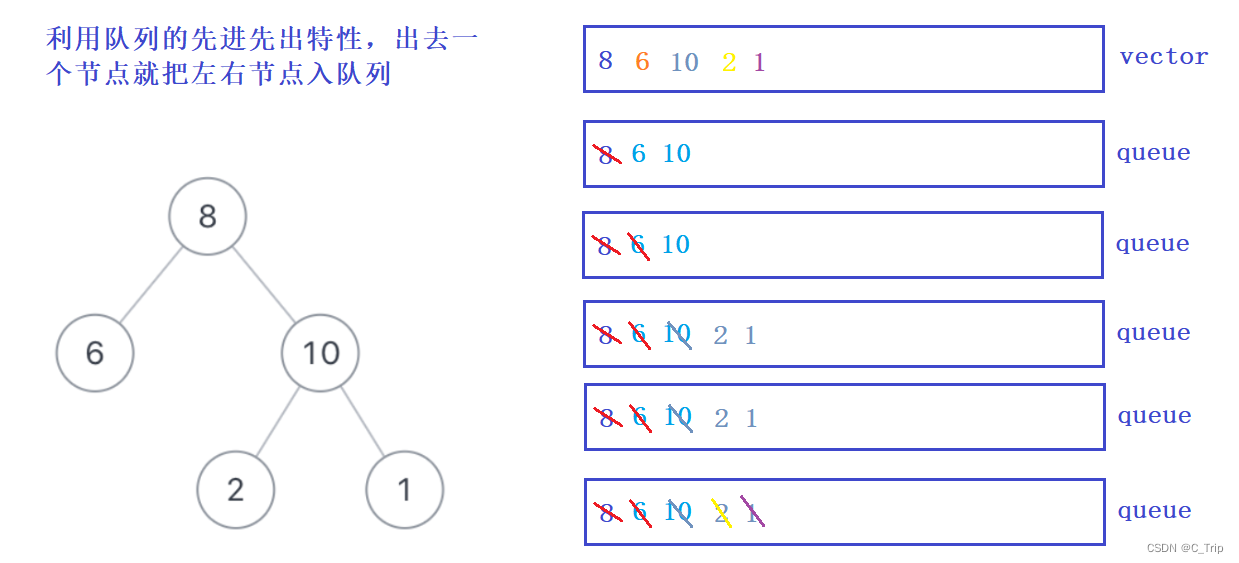
代码：

class Solution {
public:
    vector<int> PrintFromTopToBottom(TreeNode* root) {
		vector<int> result;
		if(root == nullptr)
			return result;

		queue<TreeNode*> qe;
		qe.push(root);
		while(!qe.empty())
		{
			TreeNode* front = qe.front();
			qe.pop();
			result.push_back(front->val);

			if(front->left != nullptr) //左子树不为空将左子树入队列
				qe.push(front->left);
			if(front->right != nullptr)//右子树不为空将右子树入队列
				qe.push(front->right);
		}
		return result;
    }
};

4、二叉搜索树的后序遍历序列

本题考点： BST特征的理解 牛客链接

题目描述：
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true ,否则返回 false 。假设输入的数组的任意两个数字都互不相同。

数据范围： 节点数量 0≤n≤1000 ，节点上的值满足1≤val≤10^5 ，保证节点上的值各不相同
要求：空间复杂度O(n) ，时间时间复杂度 O(n^2)

提示：
1.二叉搜索树是指父亲节点大于左子树中的全部节点，但是小于右子树中的全部节点的树。
2.该题我们约定空树不是二叉搜索树
3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历

解题思路：

• 二叉搜索树:它或者是一棵空树，或者是具有下列性质的二叉树:若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

• 后序遍历：先左后右再根

• BST的后序序列的合法序列是，对于一个序列S，最后一个元素是x(也就是root节点),如果去掉最后一个元素的序列为T，那么T满足：T可以分成两段,前一段(左子树)小于x，后一段(右子树)大于x，且这两段（子树）都是合法的后序序列

• 验证思路就是：当前序列，及其子序列必须都满足上述定义

代码：

class Solution {
public:

    bool _VerifySquenceOfBST(vector<int>& v, int begin, int end)
    {

        //返回条件
        if(begin >= end)
        {
            //区间是在不断缩小到,走到这里说明之前的范围满足检测条件
            return true;
        }
        
        //判断逻辑
        int root = v[end];
        int i = begin;
        while(i < end && v[i] < v[end])
        {
            i++;
        }
        for(int j = i; j < end; j++)
        {
            if(v[j] < v[end])
                return false;
        }

        return _VerifySquenceOfBST(v, begin, i - 1) && _VerifySquenceOfBST(v, i, end - 1);
    }
    bool VerifySquenceOfBST(vector<int> sequence) {
        if(sequence.empty())
            return false;
        
        return _VerifySquenceOfBST(sequence, 0, sequence.size() - 1);
    }
};