快排的三种方法

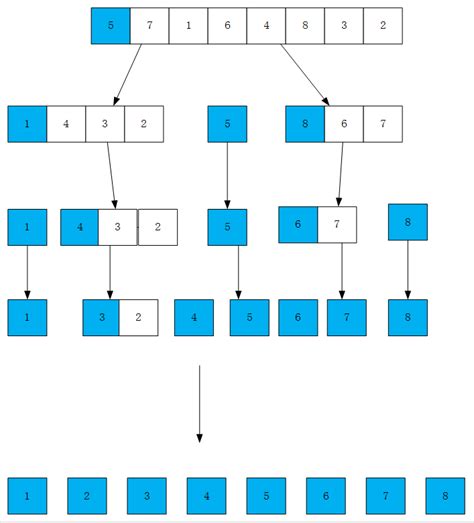
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

而对于基准值，我们一般取得是第一个元素。每执行一次微排序就确定了目前的基准值的位置，再次将基准值左边的部分和右边的部分分别进行微排序（递归），直至最终完全有序即可

1. hoare版本

微排序分析

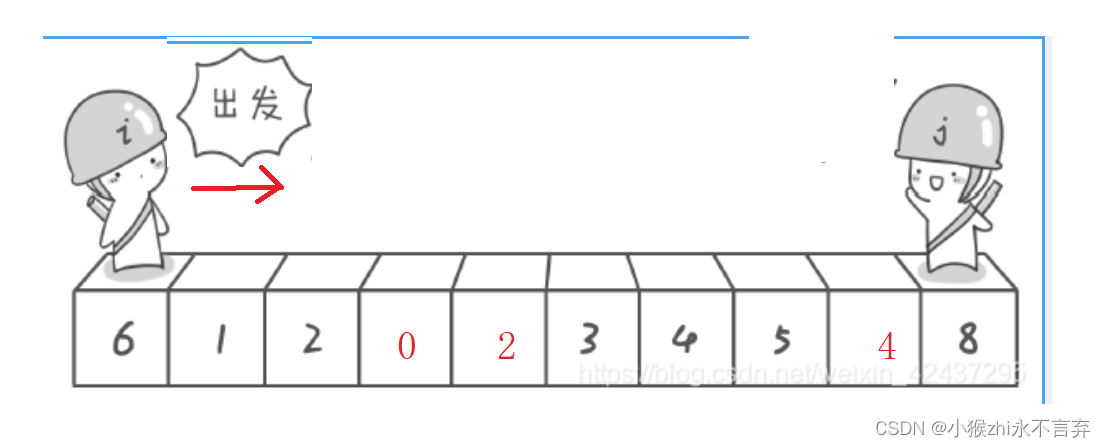
此时设定基准数（key）对应的值就是6，i 和 j分别就是从两头开始走，直到相遇就停止，此时进行最后一步，将相遇点和基准值交换，最终目的是：左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值。

所以我们就在左边找大于key的值，右边找小于key的值，找到就进行交换，此时问题就来了

1. 谁先走呢？
2. 左边是从key开始还是从下一个元素开始呢？

 

3. 最后相遇的值与基准值交换位置，那如果相遇的值大于key呢？那交换不就会出错吗？

分析问题：

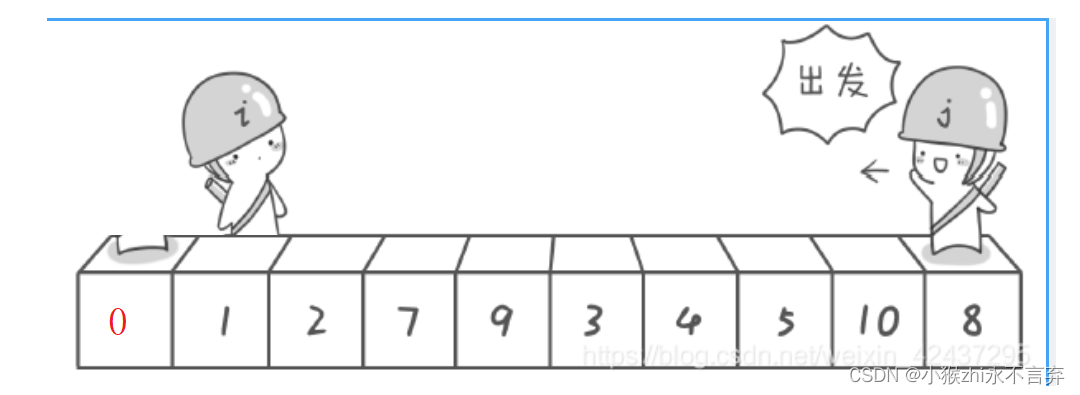
• 假如说我们不从右边开始走，而是从左边开始走，而左边是找较大值，此时下面这种情况就会相遇在数字8的位置，基准值与数字8交换，这样就出错了。但是我们如果让右边的先走，找较小值，最后就会停在较小值的位置。
• 即使是没找到的话也是和左边的基准值相遇，和自己交换，也不影响，而右边恰恰也都是大于key的值。
• 即使是在相遇之前已经发生过交换，也是将较小值换到左边，从而右边先走，最终可能相遇，相遇点是左边占着的点，也是小于key的值，交换也是将较小值换到基准值的位置。
• 但是如果左边先走找较大值，最后交换的就极可能会是较大值。所以基准值定在最左边，此时右边先走不仅是正确的交换，而且还保证的最后相遇的一定是小于基准值的值。
• 如果基准值定在最右边就得让左边的先走了。
• 假如说左值不是从基准值开始走，而是从基准值下一个位置开始走。此时下面这种情况：如果基准值是最小值的话，就会在1的位置相遇，将1与基准值交换，所以就会出错，所以左边从基准值开始走就保证了此情况。

微排序代码

int Part1Sort(int* arr, int left, int right)
{
	int keyi = left;/基准值下标
	while (left < right)
	{
		//右边找小于arr[keyi]的值
		while (left<right&&arr[right] >= arr[keyi])
			right--;

		//左边找大于arr[keyi]的值
		while (left<right&&arr[left] <= arr[keyi])
			left++;

		Swap(&arr[left], &arr[right]);
	}
	//left=right
	Swap(&arr[left], &arr[keyi]);

	return left;//返回相遇值的下标
}

外层循环条件就是 left<right，同时也要保证内部找较大较小值时 left<right，防止在找值的过程中就发生了越界，而且如果找到的值与基准值相等的话也继续找，防止左右都找到与基准值相等的值时，发生死循环的交换。

 快排递归写法

//递归部分
void QuickSort(int* arr,int left,int right)
{
	if (left >= right)
		return;
	int keyi = Part1Sort(arr, left, right);
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1,right);
}

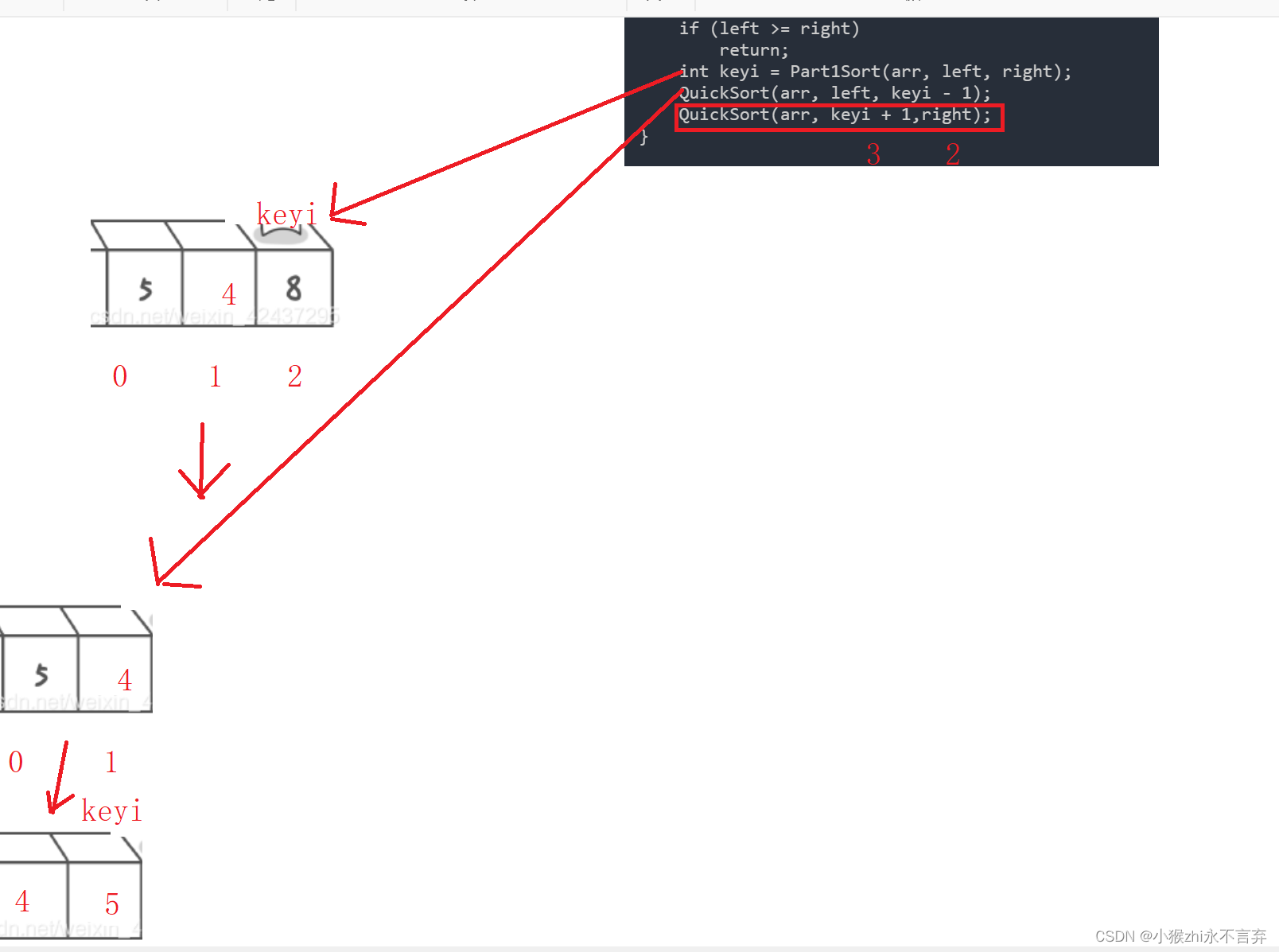
这里主要就是分析一下停止条件：即区间left和right之间只剩最后一个数或者没有数的情况

快排非递归写法（栈模拟）

void QuickSort(int* arr, int left, int right)
{
	int* stack = (int*)calloc(right,sizeof(int));//模拟栈
	assert(stack);
	int top = 0;//栈中元素个数

    //将区间存进栈里
	stack[top++] = left;//先压入左区间再压右区间
	stack[top++] = right;//所以出栈是先出右再出左

	while(top)//判断是否为空
	{
		int r = stack[--top];//出栈（右）
		int l = stack[--top];//出栈（左）
		int keyi = Part1Sort(arr, l, r);//基准值下标
		if(l<keyi-1)
		{
			stack[top++] = l;
			stack[top++] = keyi - 1;
		}
		if(keyi+1<r)
		{
			stack[top++] = keyi + 1;
			stack[top++] = r;
		}
	}
	free(stack);//防止内存泄露

}

2.挖坑法

其实挖坑法也是通过霍尔的思想改了一下，原理都是一样的，只不过更容易理解一点。就是先将基准值的值存起来，形成坑位，同样是从右边开始找较小值，找到了就将该较小值填在原来的坑里，此处形成新的坑，再从左边开始找较大值，填到坑里，并形成新的坑......最后一定是在坑中相遇，将基准值填入坑中就算完成一次微排序。

代码

int Part2Sort(int* arr, int left, int right)
{
	int key = arr[left];
	int hole = left;
	while (left < right)
	{
		//找小
		while (left<right&&arr[right] >= key)
			right--;

		arr[hole] = arr[right];//找到小于key的值就填坑
		hole = right;//形成新的坑

		//找大
		while (left < right && arr[left] <= key)
			left++;
		
		arr[hole] = arr[left];//找到对于key的值就填坑
		hole = left;//形成新的坑

	}
	//在坑的位置相遇
	arr[hole] = key;

	return hole;
}

3.前后指针法

 这种方法就是遍历一遍，将大于基准值的数向后拨。一前一后两个指针，如果cur指向的值小于基准值，就pre++再交换，如果cur指向的值大于基准值就cur++。在循环遍历的过程中始终保持着(left，right]之间的数值都是大于基准值key的，最后循环出来将left与基准值的位置交换。

代码

int Part3Sort(int* arr, int left, int right)
{
	int keyi = left;
	int pre = left;
	int cur = left + 1;
	while (cur <= right)//等于时cur指向最后一个数
	{
		if (arr[cur] <= arr[keyi])
		{
			pre++;
			Swap(&arr[pre], &arr[cur]);
		}
		cur++;

	}
	Swap(&arr[keyi], &arr[pre]);
	return pre;

}

分析优化

三数取中间值法选key

我们知道当快排遇见一组有序的数组序列时，可能就是最麻烦的，此时的时间复杂度就是O(n^2)，而正常无序的序列是O(n*log n)，所以可以看出当基准值越接近一组数据的中位数时，所花费的时间是最少的，所以就有了三数取中法选key

代码

int midi(int* arr, int left, int right)
{
	int midi = (left + right) / 2;
	if (arr[left] < arr[right])
	{
		if (arr[left] < arr[midi])//left最小
		{
			if (arr[midi] > arr[right])
				return right;
			else
				return midi;
		}
		else
			return left;
	}
	else
	{
		if (arr[left] < arr[midi])//left最小
			return left;
		else if (arr[midi] > arr[right])//left最大
			return midi;
		else
			return right;
	}
}

int tmpi = midi(arr, left, right);//将基准值放到最左边
	Swap(&arr[left], &arr[tmpi]);//将中间值设为基准值

三路划分法

当遇到完全相同的一组数据时，此时的快排就非常的慢了，每次处理一个数时间复杂度是 O(n^2)，所以就有了另一种优化方法：三路划分法，这种方法就是在快排的Hoare法和前后指针法的基础下得出的新方法。最终目的：将与基准值相同的一组数放到中间，左子区间依然是小于key的值，右子区间依然是大于key的值。

我们知道Hoare法实际就是左右数与key比较，将数据划分成三部分，而前后指针法就是从前向后遍历，将大于key的值拨到后面去。而对于三路划分其实就是基于以上思想，用到三个指针，left，cur，right 三个指针，left.基于最左边，right基于最右边，然后cur从前向后进行遍历。在移动的过程中始终尽量保证[left,cur]区间内维护的数据是等于基准值key的。

此时三路划分就是在以上基础下将与key相同的值一起拨到后面去，在将较小值换到左边，较大值换到右边

 最终l的左边是小于key的值，r的右边就是大于key的值，中间恰恰是与key相等的值。

代码

void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;

	int tmpi = midi(arr, left, right);
	Swap(&arr[left], &arr[tmpi]);

	int l = left, cur = l + 1;
	int r = right;
	int key = arr[left];
	while (cur <= r)
	{
		if (arr[cur] > key)
		{
			Swap(&arr[cur], &arr[r]);
			r--;
		}
		else if (arr[cur] < key)
		{
			Swap(&arr[cur], &arr[l]);
			cur++; l++;
		}
		else
		{
			cur++;
		}

	}

	QuickSort(arr, left, l - 1);
	QuickSort(arr, r + 1, right);
}

这种算法还可以针对自己任意设置的一个基准值进行处理，只不过cur的指向从left开始而不是left+1。一道经典leetCode题目解法就是基于该三路划分：75. 颜色分类 - 力扣（LeetCode）