CS229高斯判别分析

基本原理

在二分类中逻辑回归是通过不断优化$\theta$参数，找到最合适的分类界限。而高斯判别分析法采用先通过数据特征建立类别模型，然后在寻找分界线分类。
简单来说我们要进行区分猫和狗，逻辑回归分析法就是找到猫和狗的分界线，当新的猫狗要判断这种方法只会确定猫狗在分界线的那一边，也就说它并不能解释什么是猫什么是狗。而高斯判别分析是一种生成学习方法，通过猫狗的数据，建立起猫和狗的模型我们会知道什么是猫什么是狗，当新的数据进来时我们将数据样本和猫狗模型分别对别，看它与哪一个模型相似。
判别学习算法直接学习计算$p(y|x)$,试图学习从输入X直接映射到标签{0，1}。而生成学习算法试图通过建立模型$p(x|y)$,然后通过贝叶斯算法计算$p(y|x)$。这里$p(x|y=0)$是狗的特征分布模型，$p(x|y=1)$是猫的特征分布模型，通过贝叶斯公式推导：

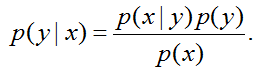
这里的分母$p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0)$,我们计算只要值的大小并不用计算分母。

算法详解

假设数据x∈R^n且是连续的，$p(x|y)$是高斯特征分布的。

在此介绍一下多元高斯分布（Multivariate Gaussian Distribution）：
if Z~N(u,$\Sigma$),Z$\in R^n,u\in R^n,\Sigma \in R^{nn}$则：
E[z]=u
cov(z)=E[(z-u)(z-u)t]=$Ez{z}^T-EzE{z}^t$(协方差矩阵）
$p(z)=1/(2{\pi }^{n/2})|\Sigma {|}^{1/2}exp(-1/2(x-u{)}^T\Sigma (x-u))$

高斯判别模型：
当我们有一个输入特征$x$是连续值随机变量的分类问题时，我们然后可以使用高斯判别分析（GDA）模型，这个模型使用多元正态分布建模$p(x|y)$。模型为：

他的分布为：

这里，我们的模型的参数是$\varphi ,u_0,u_1,\Sigma$,（注意，尽管模型中有两个不同的$u_0,u_1$,但这个模型被使用时只使用一个协方差矩阵$\Sigma$)。数据的log似然为：

给出。通过参数最大化似然函数，我们发现参数的最大似然估计为：

具体过程如下：

形象的，算法在做如下所示：

图形中显示的是训练集和两个已经拟合了两类数据的高斯分布的轮廓。注意，两个高斯分布有相同形状和朝向的轮廓，因为他们共有一个协方差矩阵$\Sigma$,但是他们有不同的均值$u_0，u_1$。图形中也显示了一条给出决策边界的直线，在直线上$p(y=1|x)=0.5$。在边界的一侧，我们预测y=1是最有可能的结果，在另一侧，我们预测y=0是最有可能得到结果。

GDA和逻辑回归

GDA模型回归同逻辑回归有一个有趣的关系，如果我们把$p(y=1|x;\varphi ,u_0,u_1,\Sigma )$看作是x的函数，我们将会发现它可以被表示为;

推导过程如下：

这样的形式，在这里$\theta$是某个适合$\varphi ,u_0,u_1,\Sigma$的函数，这恰好是逻辑回归——一个判别算法——用来建模$p(y=1|x)$的形式。
注意这里GDA相比较逻辑回归他的条件更加苛刻，也就是说GDA中$p(x|y)$服从多元高斯分布，然后我们可以说$p(x|y)$必然是一个逻辑回归。但是反过来说是不成立的。
所以说当$p(x|y)$更好的服从多元分布时，使用GDA方法最合适。一般来讲随着样本数量的增加，$p(x|y)$会更倾向于高斯分布，所以当存在大量的训练样本时，使用GDA会取得很好的效果。但是当训练样本数量较少时，GDA的鲁棒性并不强，对非高斯分布的数据处理效果并不好，而这是逻辑回归可以做的更好。

参考链接：
https://blog.youkuaiyun.com/zhulf0804/article/details/52345987
https://www.zybuluo.com/evilking/note/964503