SFT的本质，其实是在优化RL目标的下界...-优快云博客

原文链接：https://zhuanlan.zhihu.com/p/1950847739404456574

点击下方卡片，关注“大模型之心Tech”公众号

本文只做学术分享，如有侵权，联系删文，欢迎添加小助理微信AIDriver004做进一步咨询

TL；DR：本文推导出在稀疏奖励的情况下，标准 SFT 的训练目标其实是 RL 目标的一个（松的）下界，为了收紧这个下界同时保持训练稳定，作者引入了一个桥梁分布来进行调节。最终在形式上得到了一个重要性加权版本的 SFT 目标。

论文链接：https://arxiv.org/abs/2507.12856

SFT 的优化目标是 RL 的下界

首先，我们通过目标函数的推导，将 SFT 和 RL 联系起来。

RL 策略梯度算法中，训练策略模型的目标函数为：

其中是一条采样轨迹，是轨迹的的累积奖励，是参数化模型采样得到轨迹的概率，是一组轨迹的集合。

我们知道，RL 和 SFT 最主要的差异就是训练数据的分布。SFT 中，我们是有一组固定的标注数据，比如人类手写的回复或者预训练大模型生成的回复，SFT 在这些标注数据上进行模仿学习的训练。从 RL 的视角来看，相当于离线地从某个参考分布中采样轨迹，然后过滤出其中优质的样本。RL 的数据则是在线地采样当前模型的回复，根据奖励函数给出的奖励值优化策略模型，提升高奖励值的样本被采样出的概率。

为了将 RL 和 SFT 联系起来，我们首先对 RL 训练目标（式 1）应用重要性采样，将期望的分布从在线采样的（其实写作更方便对比理解？）转换为离线采样的：

接下来一步是关键，对重要性采样的系数
应用不等式：

这里绿色部分都是与参数无关的，可以把他们都放在一个常数项中。

在 SFT 的设定下，我们只有 “好的” 回复数据。从 RL 的视角来看，这可以理解为我们有一个打分函数能够区分出好的回复和差的回复，并据此构建一个奖励函数，只对打分值为正的样本给出奖励值 1，其他样本奖励值均为 0。这个稀疏的奖励函数可以从完整采样空间中过滤出 “好的” 回复数据。这里的就是 SFT 设定下的标注数据集，从而有：

上式右侧就是标准的 SFT 目标函数，至此我们推导出结论：在稀疏奖励的设定下，SFT 的优化目标是 RL 的一个下界。

从 RL 的视角来看，这个结论说明标准的 SFT 训练确实是会有一定效果的，因为它真的在优化 RL 策略梯度目标的一个下界。但是，SFT 目标作为一个下界，影响性能的另一个关键点在于这个下界够不够 “紧”。

遗憾的是，标准 SFT 情况下，这个下界可能不够紧，并且在训练过程中，随着与的差异越来越大，这个下界会越来越松，即离真正的 RL 目标越来越远。更遗憾的是，在标准的 SFT 中，我们无法调整和优化这个下界紧的程度，因为在式 2 中，没有任何可以由我们自主调整的项。

引入桥梁分布 q

现在我们已经推导出 SFT 的优化目标是 RL 的一个下界，但是也发现随着训练的进行这个下界越来越松。那么我们应该如何调整 SFT 的训练目标才能改进这一点呢？

iw SFT 的方案是：引入一个辅助分布，作为一个可调整的项，选择合适的，在收紧这个下界的同时，保持训练的稳定，从而优化 SFT 的训练。

具体来说，我们引入一个辅助分布，这个分布的形式可以随便选，具体怎么选，涉及到稳定训练与收紧下界的权衡，后面会讨论。现在有了这个辅助分布，我们可以将 RL 的训练目标重写为：

对应用同样的不等式，得到：

这样就得到了一个重要性加权（Importance Weighted） 的 SFT 形式 iw SFT：

这个形式相比于原来的 SFT 目标，多了一个权重系数，其中是固定的，但是是我们可以自由设置的，通过调整辅助分布，我们就可以收紧这个下界。接下来的关键问题就是：如何选择分布的形式呢？

如何选择 q

我们先来看一下 iw sft 的性质。不等式当且仅当时取得等号，当趋近于时，趋近于 1，从而趋近于 RL 目标。也就是说分布越接近于，iw sft 作为的下界越紧，这是我们想要的。

但是如果简单地取，那么随着训练的进行又会离越来越远，方差越来越大，重要性采样变得不稳定，最终导致训练不稳定。因此，我们在追求更紧下界的同时，还要保证和差异不要太大，即，以稳定训练。这是基于重要性采样的这类方法要面临的经典问题。

总之，分布具体形式的选择，既要尽可能接近，从而保证下界足够紧，又不能离太远，从而保证方差比较小，来稳定训练。最终，作者采用了如下的形式：

其中是策略模型参数的一个时间滞后（可以直接更新也可以 EMA 更新）的版本，这样就能保证训练过程中与比较接近，从而有比较紧的下界。同时，在训练过程中，还需要约束重要性权重来控制的迭代（从而间接地控制），从而保证训练的稳定性。具体如何约束呢？作者提出了两种不同的方案。

第一种方案是每步裁剪重要性权重。要将重要性权重控制在一个范围内，直接裁剪是最直接的方式，在 token 维度裁剪：

然后对轨迹维度的重要性权重进行一个整体的裁剪：

第二种方案是平滑重要性权重。通过在轨迹维度对重要性权重进行平滑，来保证其方差较低。具体来说，取：

其中是轨迹中 token 的索引，是一个单调递减函数。

这两种约束方法的细节可以在原文实验部分查看。iw SFT 的具体算法如下所示，其中关键就是权重系数的计算。

例子

思考一个多臂老虎机的例子，有两个选项：拉左杆和拉右杆，奖励函数是：对于拉右杆一定给出 1 的奖励值，而对于拉左杆则有 50% 概率奖励值为 1，50% 的概率奖励值为 0：

显然，上帝视角下，最优的策略是一直拉右杆。

假设我们的参考策略是等概率地选择拉左杆和拉右杆，那么在 SFT 的设定下，我们从过滤出好的动作组成数据集。在这种均匀分布的参考策略下，的数据中，拉右杆的次数会是拉左杆的两倍，即 1/3 拉左杆和 2/3 拉右杆。

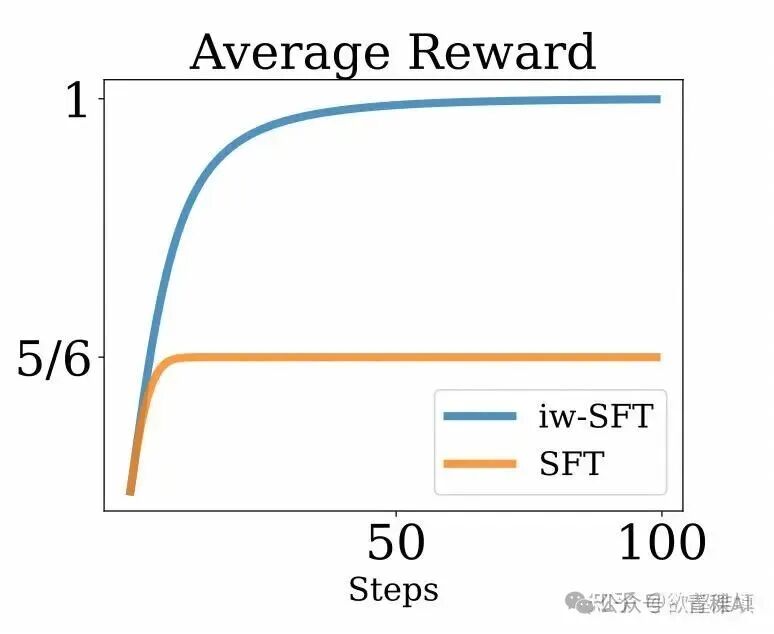
接下来，如果我们在数据集上进行标准的 SFT 训练，最终学习到的模型会有 1/3 的概率拉左杆，2/3 的概率拉右杆，这样最终得到的期望奖励值为 5/6。虽然相较于参考策略好了不少，但离最优策略还有差距。这里 SFT 学习不到最优策略的的原因很明显：SFT 无法有效地利用（被过滤掉的）负样本的信息。所以说虽然 SFT 目标是在优化 RL 目标的一个下界，并且可以在参考策略的基础上进一步提升，但最终还是无法通向最优的策略。