Diffusion²：一个双扩散模型，破解自动驾驶“鬼探头”难题！

点击下方卡片，关注“自动驾驶之心”公众号

戳我-> 领取自动驾驶近30个方向学习路线

>>自动驾驶前沿信息获取→自动驾驶之心知识星球

论文作者 |  Yuhao Luo等

编辑 | 自动驾驶之心

同济大学和威斯康星大学麦迪逊分校最近的一篇工作，很有意思分享给大家。这篇工作指出一个问题：当行人突然从盲区出现时，往往无法获得足够的观测数据（即瞬时轨迹），因此交通事故的风险很高。换句话说就是鬼探头的场景，如何做好行人的轨迹预测。

针对这个问题，他们提出了Diffusion² - 专为瞬时轨迹预测而设计。Diffusion²由两个串联的扩散模型组成：一个用于反向预测，生成未观测到的历史轨迹；另一个用于正向预测，预测未来轨迹。考虑到生成的未观测历史轨迹可能会引入额外的噪声，提出了一种双头参数化机制来估计其偶然不确定性（aleatoric uncertainty），并设计了一个时间自适应噪声模块，该模块在前向扩散过程中动态调节噪声尺度。实验证明，Diffusion2在ETH/UCY和斯坦福无人机（Stanford Drone）数据集上的瞬时轨迹预测任务中树立了新的最先进水平。

• 论文标题: Diffusion²: Dual Diffusion Model with Uncertainty-Aware Adaptive Noise for Momentary Trajectory Prediction

• 机构: 威斯康星大学麦迪逊分校、华盛顿大学、同济大学

• 论文链接：https://arxiv.org/abs/2510.04365

背景回顾与主要贡献

准确的行人轨迹预测对于自动驾驶至关重要，因为它增强了车辆的安全性，尤其是在涉及人车交互的场景中。近年来，很多算法都在尝试解决这一任务。通常这些方法侧重于基于足够长的观测期（例如8帧，约3.2秒）来预测未来轨迹。然而，在许多现实场景中，例如当行人突然出现在障碍物（如建筑物或卡车）后方时，车辆没有足够的时间来收集充分的观测数据。这对传统的预测方法提出了巨大挑战，常常导致预测性能显著下降，甚至增加了交通事故的风险。在SDD数据集中，仅有瞬时观测的行人的出现频率达到2.22 s⁻¹，在ETH/UCY数据集中为1.02 s⁻¹。因此，研究仅使用有限观测数据的行人轨迹预测至关重要。

尽管已有工作证明联合预测历史轨迹以丰富上下文信息、弥补瞬时观测局限性的有效性，但它同时共同预测历史和未来轨迹，忽略了这两个组成部分之间的因果关系。在本研究中，我们以顺序方式分别预测历史和未来轨迹。具体而言，我们提出了一种名为Diffusion2的模型，用于瞬时行人轨迹预测。在扩散模型优势的基础上，我们的框架采用了两个串联的组件：一个用于反向预测，另一个用于正向预测，如图1所示。

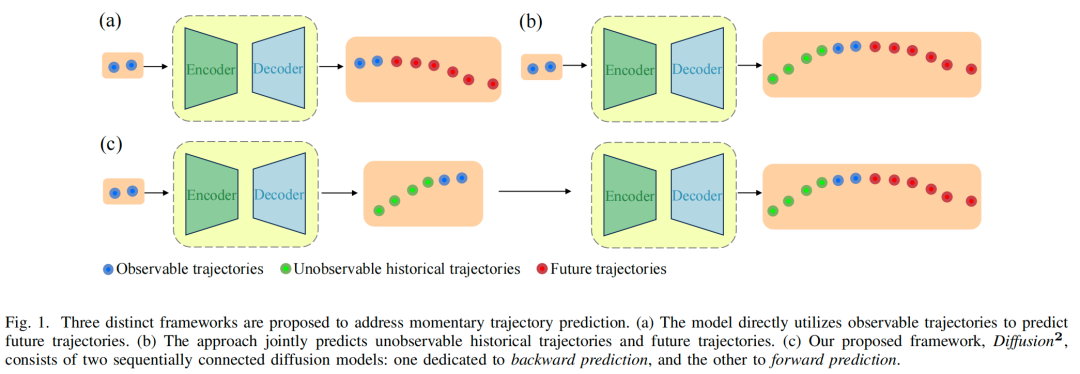
随之而来的一个问题是预测出的历史轨迹的可靠性：如果它们高度不准确或包含噪声，则可能对后续的未来轨迹预测产生不利影响。因此，量化预测历史轨迹的不确定性并选择性地利用可靠信息进行下游预测任务至关重要。然而，扩散模型仅隐式地学习数据分布，缺乏显式量化不确定性的能力。为了填补这一空白，我们设计了一种双头参数化机制，该机制通过引入两个输出头来增强标准的噪声预测网络。

第一个头预测噪声，第二个头则估计每个坐标的对数方差，从而能够直接量化偶然不确定性。

随后，为了结合估计的偶然不确定性，我们设计了一个时间自适应噪声调度器，它根据预测的不确定性水平，动态地将噪声注入到前向扩散模型中。直观上讲，当历史轨迹高度不确定时，会向正向扩散模型注入更多噪声，以鼓励生成过程中的探索；而当不确定性较低时，则减少噪声的添加。

总而言之，我们研究的主要贡献如下：

• 提出了Diffusion²，这是一个新颖的框架，由两个顺序的扩散模型组成，能够捕捉轨迹的因果依赖性：一个用于反向预测，另一个用于正向预测。

• 提出了一种双头参数化机制，使反向预测的扩散模型能够在单次采样中量化偶然不确定性，并进一步为正向预测扩散模型引入了一种自适应噪声调度策略，该策略根据估计的不确定性动态调整噪声的大小。

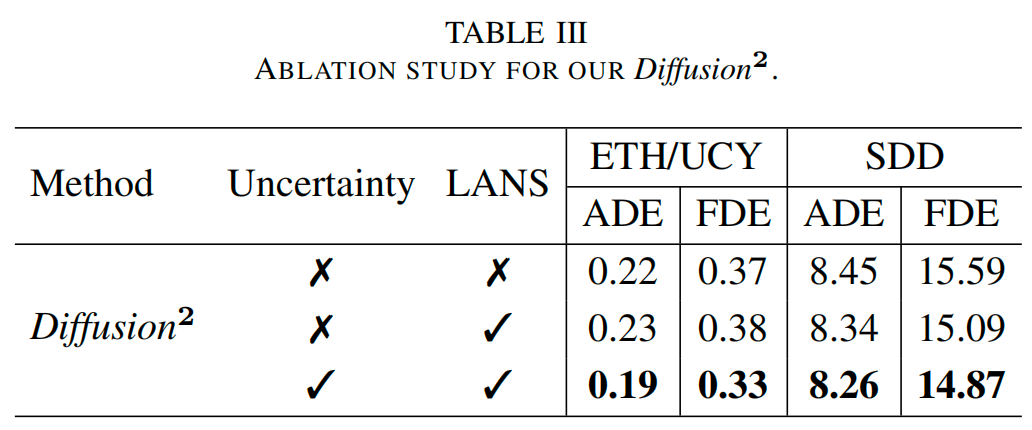
• Diffusion²在瞬时行人预测中实现了SOTA，这一点在ETH/UCY和斯坦福无人机数据集上的实验得到了证实。

预备知识

A. 问题定义

在本研究中，我们的目标是仅使用两帧观测数据作为输入，进行准确的瞬时行人轨迹预测。这些观测帧被定义为  ，其中   表示自车行人的二维位置，  代表周围行人的位置，  表示周围行人的数量，而   对应语义场景图。目标是预测未来轨迹  ，其中   表示预测时间范围。此外，我们将未观测到的历史轨迹定义为  ，其中   是未观测历史轨迹的长度。我们的模型通过利用基于少数观测点推断出的历史轨迹来预测未来轨迹。由于推断出的历史轨迹可能带有噪声，我们的模型也需考虑其不确定性。

B. 去噪扩散概率模型

去噪扩散概率模型 (DDPM)通常由两个马尔可夫链过程组成：一个前向扩散过程和一个反向去噪过程。为了避免冗余，我们仅展示对   的扩散公式，并指出该过程可直接应用于  。

前向扩散过程通过在多个时间步上添加高斯噪声，逐渐破坏真实数据，形成一系列扰动样本  ，其中   是原始数据，  是扩散步数。通常，我们将扩散过程定义为：

其中  ， ，  表示标准差（因此协方差为  ）。扩散参数   在时间步上诱导了一个噪声调度，使得信噪比 (SNR)   在   上严格单调递减。

相反，反向去噪过程被训练为沿着这个马尔可夫链逐步、迭代地去除噪声，从而在上下文信息的条件下重建原始轨迹。通常，我们将反向去噪过程定义为：

其中  ，且  ；  表示用参数   近似   的神经网络，  是用作起点的标准高斯噪声。此外，  和   分别表示预测的均值和方差。

算法详解

A. 整体架构

我们提出的模型 Diffusion2 是一个两阶段的扩散框架，由两个顺序连接的模块组成：DDPMpast 和 DDPMfut。如图 2 所示，DDPMpast 负责反向轨迹预测并估计偶然不确定性，而 DDPMfut 则用于预测未来轨迹。给定观测帧  ，一个共享编码器首先提取上下文表征  。在   的条件下，DDPMpast 同时预测未观测到的历史轨迹   并通过双头参数化机制估计其偶然不确定性  。随后，我们采用一个由两个 LSTM 层和一个三层 MLP 组成的轨迹编码器，从   中提取特征  。提取出的特征   与上下文表征   融合，形成一个新的条件向量  ，该向量作为 DDPMfut 的输入上下文来预测未来轨迹  。

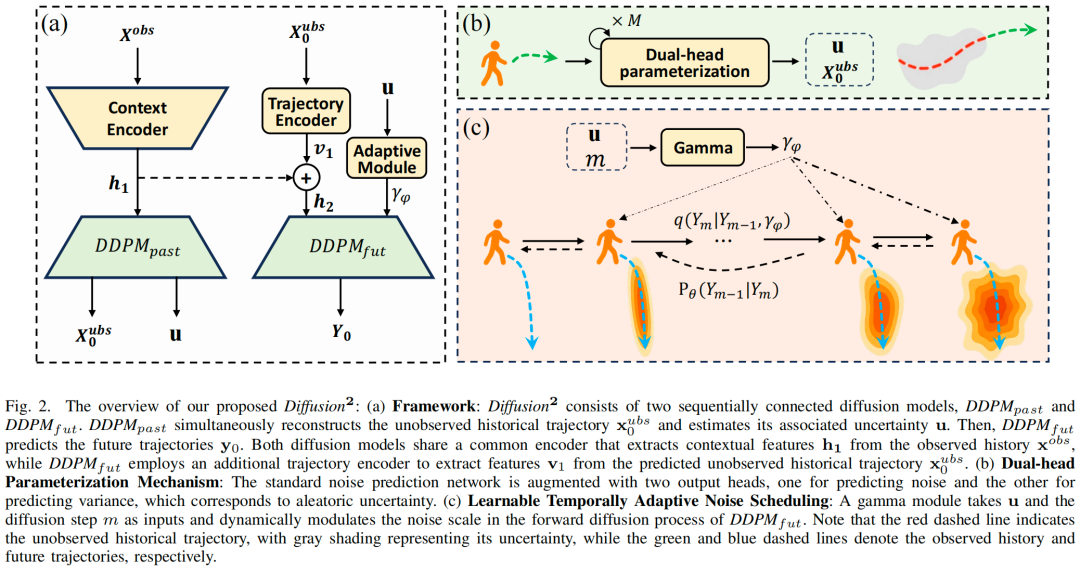
此外，为了结合所估计的偶然不确定性，我们为 DDPMfut 引入了一种可学习的时序自适应噪声调度策略，其中伽马模块（gamma module）根据   和当前扩散时间步   动态调整噪声尺度。需要注意的是，设计一个复杂的网络来从轨迹中提取时空特征并非本工作的重点，Diffusion2 是一个对编码器不敏感的框架，可以无缝集成先前研究中提出的各种编码器。在我们的实验中，我们采用了MOE 编码器，因为它具有卓越的表征能力。

对于 DDPMpast 和 DDPMfut 的去噪骨干网络，我们采用了一个简化的 Transformer 解码器。并行的全连接层首先将被破坏的轨迹样本及其上下文特征投影到一个共同的潜在空间，然后添加当前扩散时间步的正弦编码。这个序列随后由三个堆叠的自注意力块处理，以捕捉时空依赖性。最后，一个线性层将该表征映射回二维坐标空间。

B. 双头参数化

在这项工作中，为了高效地量化预测出的未观测历史轨迹的偶然不确定性，我们设计了一种双头参数化机制，该机制增强了标准的噪声预测网络，使其输出两个头：

其中   表示 DDPMpast 的学习参数。第一个头   预测缩放后的高斯噪声，这与标准扩散模型中的做法相同；而第二个头   则直接在每个坐标上预测对数方差。为简洁起见，在下文中我们将   简写为  ，将   简写为  。在推理阶段，双头参数化无需蒙特卡洛平均即可传播不确定性。我们将反向过程更新如下：

其中   表示将向量映射为其元素构成的对角矩阵的算子，  和   分别表示 DDPMpast 预测的均值和协方差。应用 Tweedie 公式可得到最终预测   的闭式方差：

第一项捕捉了数据相关的偶然不确定性，而第二项则解释了由调度器引入的已知噪声。为了分离出内在的不确定性，可以减去第二项。值得注意的是，双头参数化机制是为 DDPMpast 设计的。

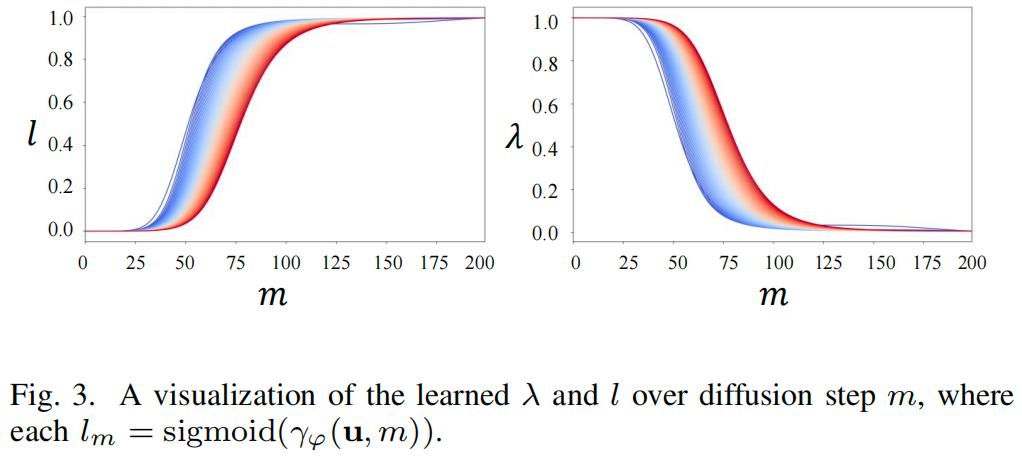
C. 时序自适应可学习噪声调度

传统的扩散框架由于其预设的前向噪声调度，往往难以利用已知的数据特征。为了弥补这一差距，我们设计了一种感知不确定性的时序自适应噪声调度，它引导扩散过程更好地捕捉特定于样本的结构，并改进数据分布建模。具体而言，我们利用预测的历史轨迹的不确定性来调整噪声调度。

自然地，这种噪声调度的前向过程定义为：

其中   且  。那么，

去噪过程给出为：

其中   表示 DDPMfut 的参数。我们通过一个有界的对数信噪比（log-SNR）场   来控制前向动态。给定  ，扩散参数恢复为  ， ，以及  。这里，  定义为：

其中   是关于   的单调五次多项式：

此参数化强制边界条件   和  。我们将系数预测器实现为一个包含两个 LSTM 层和一个两层 MLP 的神经网络。该网络输出三个系数向量  。我们设置   和  。此处   表示一个常数。

D. 损失函数

扩散概率模型 (DDPM) 的损失函数源自数据负对数似然的变分下界 (VLB)。本文中的 Diffusion2 由两个顺序连接的扩散模型组成。因此，总损失函数自然地分解为两个部分，每个部分对应一个方向的预测。

DDPMpast 的损失。 对于反向预测，我们设计了双头参数化机制，使扩散模型能够同时估计均值和偶然不确定性。具体来说，过去分支的单步反向转移如公式 (8) 所示，其以   参数化的均值和对角协方差由公式 (9) 和 (10) 给出。自然地，第   步的证据下界 (ELBO) 贡献是高斯负对数似然：

其中   也包含了与可学习参数无关的项。将公式 (9) 中的   替换为真实噪声  ，可以定义后验均值  ，它们之间的差值为：

将 (19) 代入 (18) 的二次型并利用   的对角结构，所有仅与调度相关的因子都坍缩为常数，只留下参数依赖的精度加权项   作用于   残差上。类似地，对数行列式也得以简化，因为   是对角矩阵。丢弃与   和   无关的项后，我们得到需要优化的异方差高斯负对数似然：

第一项在   空间中执行精度加权回归，而第二项是   正则化项，防止出现方差趋近于零（过度自信）的解。

DDPMfut 的损失。 对于正向预测，我们将单步条件概率定义为公式 (13)，其中   和   由公式 (14) 和 (15) 给出。在我们基于上下文的高斯转移定义下，前向过程是

给定   和干净目标   时，  的相应条件分布为

其中   等于公式 (15)，即  。 在协方差匹配的情况下，ELBO 项简化为两个仅均值不同的高斯分布之间的 KL 散度：

因为

我们定义（基于上下文的）后验精度如下：

丢弃与   无关的常数项，并对时间步进行期望（例如，通过均匀采样  ）后，得到用于正向分支的训练损失：

因此，总损失函数  ，训练阶段如算法 1 所示。

E. 模型推理

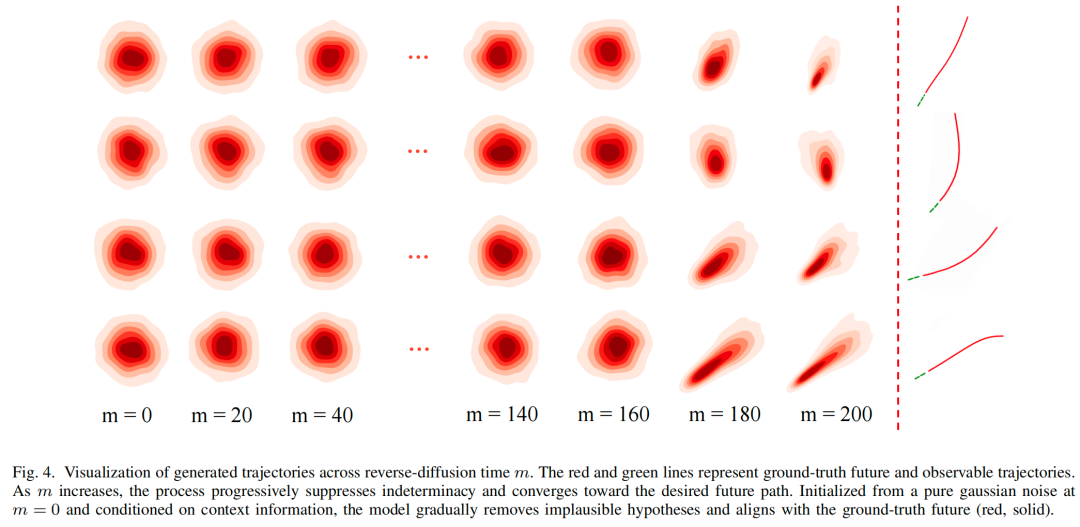
前面的章节详细介绍了模型架构和训练过程。一旦训练完成，我们就可以使用 Diffusion2 来生成未来的行人轨迹。

在第一阶段，DDPMpast 通过对纯高斯噪声   进行去噪，来获得合理的未观测轨迹。去噪过程如下：

其中   和  。同时利用 Tweedie 公式，我们可以得到最终预测   的闭式方差，如公式 (11) 所示。

在第二阶段，我们采用 DDPMfuture 的去噪过程，从纯高斯噪声   预测出合理的未来轨迹。具体来说，从   开始，我们迭代如下：

其中  。总结来说，推理过程如算法 2 所示。

实验结果

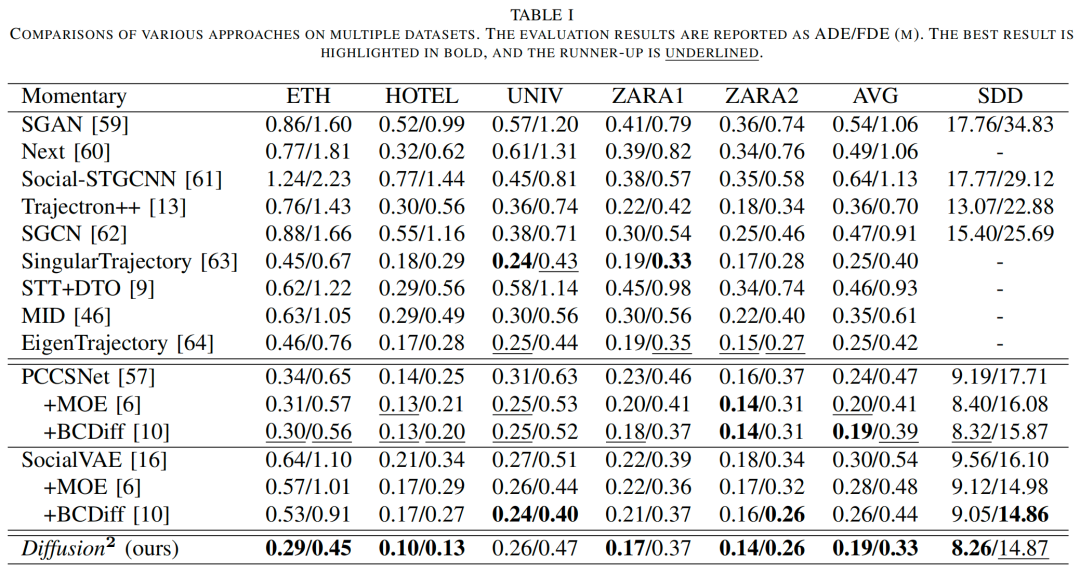
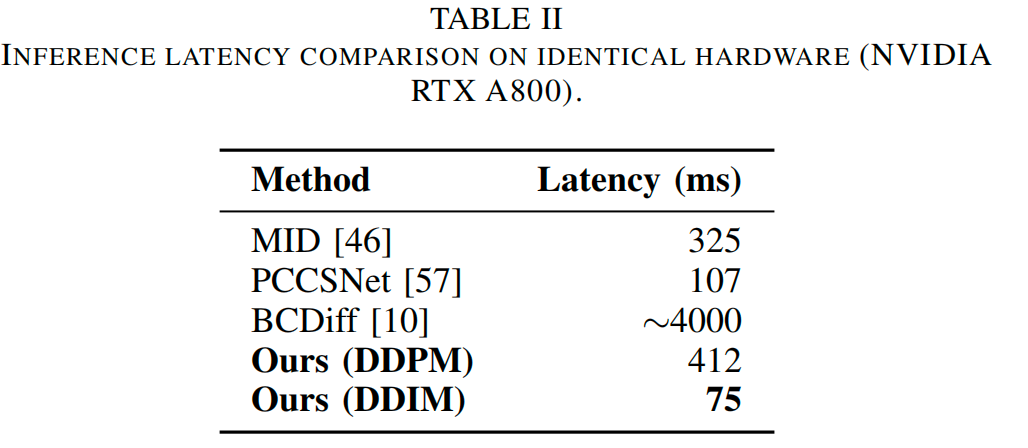
结论与讨论

在本研究中，我们提出了一种名为 Diffusion2 的全新框架，专为瞬时轨迹预测而设计。我们提出的模型由两个顺序连接的扩散模型组成：一个用于生成未观测到的历史轨迹，另一个用于预测未来轨迹。考虑到预测出的历史轨迹可能引入噪声，我们设计了一种双头参数化机制来估计其不确定性，并设计了一个可学习的自适应噪声模块，在前向扩散过程中动态调整噪声尺度。实验证明，我们的 Diffusion2 在多个数据集上均优于现有的最先进方法。

同时，我们也注意到，基于扩散的框架存在固有的局限性。特别是，其迭代采样过程导致推理速度较慢，这可能会阻碍其在实时场景中的部署。此外，由于训练过程涉及优化多个扩散阶段，计算成本可能很高。

在未来的工作中，我们计划探索更高效的训练和推理方法，以降低计算资源开销，同时保持预测质量。

局限性。 

尽管 Diffusion2 取得了良好的结果，但它仍然存在局限性。我们观察到在交互密集的场景（例如 UNIV 数据集中的场景）中，其适应能力有所下降。在未来的工作中，我们将改进其效率和鲁棒性，并在更复杂的交通场景中验证该框架的有效性。

自动驾驶之心

论文辅导来啦

自驾交流群来啦！

自动驾驶之心创建了近百个技术交流群，涉及大模型、VLA、端到端、数据闭环、自动标注、BEV、Occupancy、多模态融合感知、传感器标定、3DGS、世界模型、在线地图、轨迹预测、规划控制等方向！欢迎添加小助理微信邀请进群。

知识星球交流社区

近4000人的交流社区，近300+自动驾驶公司与科研结构加入！涉及30+自动驾驶技术栈学习路线，从0到一带你入门自动驾驶感知（大模型、端到端自动驾驶、世界模型、仿真闭环、3D检测、车道线、BEV感知、Occupancy、多传感器融合、多传感器标定、目标跟踪）、自动驾驶定位建图（SLAM、高精地图、局部在线地图）、自动驾驶规划控制/轨迹预测等领域技术方案、大模型，更有行业动态和岗位发布！欢迎加入。

独家专业课程

端到端自动驾驶、大模型、VLA、仿真测试、自动驾驶C++、BEV感知、BEV模型部署、BEV目标跟踪、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、车道线检测、轨迹预测、在线高精地图、世界模型、点云3D目标检测、目标跟踪、Occupancy、CUDA与TensorRT模型部署、大模型与自动驾驶、NeRF、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频

学习官网：www.zdjszx.com