本文详细介绍了利用遗传算法解决二维函数优化问题的过程，包括编码方式、适应度函数、选择、交叉和变异操作的实现。作者通过C++实现了遗传算法，并对编码方式进行了优化，以适应问题约束。在运行过程中，发现算法的解并不稳定，可能存在轮数不足、交叉和变异操作过于朴素等问题。作者反思并提出可能的改进措施。
一、问题概览
利用遗传算法求解下述问题的最优解：
minff(x1,x2)=100(x12−x2)2+(1−x1)2−2.048<=xi<=2.048,i=1,2
minf\\
f(x_1,x_2) = 100(x_1^2 - x_2)^2+(1 - x_1)^2\\
-2.048<=x_i<=2.048,i = 1,2
minff(x1,x2)=100(x12−x2)2+(1−x1)2−2.048<=xi<=2.048,i=1,2
二、建模过程
1 编码方式
假设精度为1e-3，那么对单个变量xi来说，我们需要编码的个数就是2.048 * 1e3 - (-2.048) * 1e3 + 1,总共有4097个可行解，如果采用二进制编码，则需要13个二进制位(2^13 = 8192)才能表示，如果把每一种状态用一个二进制位来表示，则需要4097个二进制位，这显然太多了；然而前者用13个二进制位的代价是所有高位为1的状态除1 0000 0000 0000都不合法，每次交叉和变异时都要检查，所以我的编码建模思路对其进行了改进，如下：
我使用12个二进制位对单个变量xi进行编码，映射方式为下列公式：
xi=−2.048+0.001∗to_ulong(bitset(xi))
x_i = -2.048 + 0.001 * to\_ulong(bitset(x_i))
xi=−2.048+0.001∗to_ulong(bitset(xi))
其中to_ulong表示将xi的二进制表示bitset(xi)转化为对应的十进制数，那么显然采用这种编码方式时，xi的取值范围只有
−2.048<=xi<=2.047
-2.048<=x_i<=2.047
−2.048<=xi<=2.047
但是没有关系，我们可以先将xi = 2.048情况的最好解得到，遗传算法得到跑完最后结果后，再与其进行比较，取更好结果为最终遗传算法的解。
在C++中，操纵指定个数的二进制位的一种数据结构是std::bitset，所以我们用一个类封装一个一个bitset表示其为染色体。
利用rand()%2来生成初始随机的单个染色体，解码就按照我们的映射方式解码，顺便可以加上变异操作，利用bitset的flip成员函数，它可以指定某一个二进制位进行取反，我们利用rand() % 12获得指定二进制位，然后调这个函数即可。
// 染色体
class chromosome
{
public:
// 构造函数内进行随机生成编码
chromosome()
{
for (int i = 0; i < 12; ++i)
{
bitcode[i] = rand() % 2;
}
}
// 解码
double decode()
{
UL val = bitcode.to_ulong();
double res = -2.048 + 0.001 * val;
return res;
}
// 变异操作
void variation()
{
bitcode.flip(rand() % 12);
}
bitset<12> bitcode;
};
顺便封装一个个体的结构体，它拥有两个染色体，表示x1和x2的编码。
// 两个染色体表示x1的编码和x2的编码 表示一个个体
struct Individual
{
chromosome code1;
chromosome code2;
};
2 适应度函数与选择操作
我们采用标准的轮盘赌局算法设计适应度函数，定义适应度函数
g(i)=1f(xi1,xi2),f!=0else,g(i)=1e9
g(i) = \frac{1}{f(x_{i1}, x_{i2})},f!=0\\
else,g(i) = 1e9
g(i)=f(xi1,xi2)1,f!=0else,g(i)=1e9
然后计算其每个个体被选中的概率：
Pi=gi∑gi
P_i = \frac{g_i}{\sum g_i}
Pi=∑gigi
然后计算其前缀和数组q:
qk=∑i=0kPi
q_k = \sum _{i=0}^{k}P_i
qk=i=0∑kPi
然后每轮选择时，随机生成一个0到1的随机数r，我们选满足q(i - 1) < r <= q(i)的个体i入下一轮种群。
而算法基础课有一种算法非常适用于这种有序序列中的查找：二分查找，这一步我们可以用二分查找进行，时间复杂度是O(logN)，比通常的遍历一遍O(N)要快很多。
重复上述操作N次，选出下一代种群。
// 计算f(个体x)的值
double f(Individual& x)
{
double x1 = x.code1.decode();
double x2 = x.code2.decode();
return 100 * (x1 * x1 - x2) * (x1 * x1 - x2) + (1 - x1) * (1 - x1);
}
vector<Individual> select(vector<Individual>& popu)
{
vector<double> F(500);
// 获取适应度函数
for (int i = 0; i < 500; ++i)
{
double myval = f(popu[i]);
if (fabs(myval) < 1e-9) F[i] = (double)1e10;
else F[i] = 1 / myval;
}
// 计算染色体i被选择的概率
vector<double> p(500);
double Fsum = accumulate(F.begin(), F.end(), (double)0.0);
for (int i = 0; i < 500; ++i)
{
p[i] = F[i] / Fsum;
}
// p数组的前缀和
vector<double> q(500);
q[0] = p[0];
for (int i = 1; i < 500; ++i)
{
q[i] = q[i - 1] + p[i];
}
int cnt = 500;
vector<Individual> res;
// 轮盘赌博
while (cnt--)
{
// 0-1的随机数
double r = rand() % N / (double)N;
// 使用二分查找 找到q中>=r的左边界
int l = 0, right = 499;
while (l < right)
{
int mid = (l + right) / 2;
if (q[mid] >= r)
{
right = mid;
}
else l = mid + 1;
}
// 向返回数组中插入选择的染色体
if (l >= 0 && l < 500) res.push_back(popu[l]);
else if (l < 0) res.push_back(popu[0]);
else if (l >= 500) res.push_back(popu[499]);
}
return res;
}
3 交叉操作
我们采用单点交叉策略，通过生成一个0到1的随机数，看其是否小于交叉概率值，如果小于，则进行交叉操作。
单点交叉操作就是自某一位开始后，交换两个染色体的后续二进制位，这个很好实现，通过rand()%12得到对应起始位置，利用for循环交换即可，注意我们每个个体有两个染色体，要和另一个个体的哪个染色体交换我们可以再来通过rand() % 2得到的值控制。
void Cross(Individual& a, Individual& b)
{
int j = rand() % 12;
int who = rand() % 2;
for (int k = j; k < 12; ++k)
{
if (who == 0)
{
bool tmp = a.code1.bitcode[k];
a.code1.bitcode[k] = b.code1.bitcode[k];
b.code1.bitcode[k] = tmp;
}
else
{
bool tmp = a.code2.bitcode[k];
a.code2.bitcode[k] = b.code2.bitcode[k];
b.code2.bitcode[k] = tmp;
}
}
}
4 变异操作
我们采用单点变异策略，每次先通过生成一个0到1的随机数判断是否能发生变异，如果能变异再通过rand() % 2判断变异哪个染色体，然后调用染色体里的变异函数进行变异。
// 3.变异操作
for (int i = 0; i < 500; ++i)
{
double r = rand() % N / (double)N;
if (r < Pm)
{
int who = rand() % 2;
if (who == 0) population[i].code1.variation();
else population[i].code2.variation();
}
}
5 总体代码框架
我们分了三个文件来组成我们的项目，Gentic.h表示用到的各种结构和函数的声明，Genetic.cpp表示这些函数的实现，main.cpp表示遗传算法主运行逻辑。
// Genetic.h
#pragma once
#include <iostream>
#include <string>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <bitset>
#include <numeric>
using namespace std;
typedef unsigned long UL;
const double gap = 1e-7;
const int N = 100000;
// 交换概率
const double Pc = 0.6;
// 变异概率
const double Pm = 0.1;
// 设置概率初始化
void probabilityinit();
// 染色体
class chromosome
{
public:
// 构造函数内进行随机生成编码
chromosome()
{
for (int i = 0; i < 12; ++i)
{
bitcode[i] = rand() % 2;
}
}
// 解码
double decode()
{
UL val = bitcode.to_ulong();
double res = -2.048 + 0.001 * val;
return res;
}
// 变异操作
void variation()
{
bitcode.flip(rand() % 12);
}
bitset<12> bitcode;
};
// 两个染色体表示x1的编码和x2的编码 表示一个个体
struct Individual
{
chromosome code1;
chromosome code2;
};
// 两个个体的交叉
void Cross(Individual& a, Individual& b);
// 函数f
double f(Individual& x);
// 放最优解的结构体
struct thebest
{
thebest(double X1 = 0, double X2 = 0)
:x1(X1), x2(X2)
{
val = 100 * (x1 * x1 - x2) * (x1 * x1 - x2) + (1 - x1) * (1 - x1);
}
thebest(double X1, double X2, double Val)
: x1(X1), x2(X2), val(Val)
{}
double x1;
double x2;
double val;
};
// 获取种群最大值
void getbest(vector<Individual>& popu, thebest& best);
// 获取例外情况(一个点是2.048)情况的最大值
void getexecpbest(thebest& execp);
// 选择函数
vector<Individual> select(vector<Individual>& p);
// Genetic.cpp
#include "Genetic.h"
void probabilityinit()
{
srand((unsigned int)time(nullptr));
}
void Cross(Individual& a, Individual& b)
{
int j = rand() % 12;
int who = rand() % 2;
for (int k = j; k < 12; ++k)
{
if (who == 0)
{
bool tmp = a.code1.bitcode[k];
a.code1.bitcode[k] = b.code1.bitcode[k];
b.code1.bitcode[k] = tmp;
}
else
{
bool tmp = a.code2.bitcode[k];
a.code2.bitcode[k] = b.code2.bitcode[k];
b.code2.bitcode[k] = tmp;
}
}
}
void getbest(vector<Individual>& popu, thebest& best)
{
thebest curbest;
for (auto& p : popu)
{
double curval = f(p);
if (curval < curbest.val)
{
double x1 = p.code1.decode();
double x2 = p.code2.decode();
curbest = { x1, x2, curval };
}
}
if (curbest.val < best.val)
{
best = curbest;
}
}
double _f(double x1, double x2)
{
return 100 * (x1 * x1 - x2) * (x1 * x1 - x2) + (1 - x1) * (1 - x1);
}
void getexecpbest(thebest& execp)
{
// x2固定为2.048
for (int i = 0; i < (1 << 12); ++i)
{
double x2 = 2.048;
double x1 = -2.048 + 0.001 * i;
double curval = _f(x1, x2);
if (curval < execp.val)
{
execp = { x1, x2, curval };
}
}
// x1固定为2.048
for (int i = 0; i < (1 << 12); ++i)
{
double x1 = 2.048;
double x2 = -2.048 + 0.001 * i;
double curval = _f(x1, x2);
if (curval < execp.val)
{
execp = { x1, x2, curval };
}
}
}
vector<Individual> select(vector<Individual>& popu)
{
vector<double> F(500);
// 获取适应度函数
for (int i = 0; i < 500; ++i)
{
double myval = f(popu[i]);
if (fabs(myval) < 1e-9) F[i] = (double)1e10;
else F[i] = 1 / myval;
}
// 计算染色体i被选择的概率
vector<double> p(500);
double Fsum = accumulate(F.begin(), F.end(), (double)0.0);
for (int i = 0; i < 500; ++i)
{
p[i] = F[i] / Fsum;
}
// p数组的前缀和
vector<double> q(500);
q[0] = p[0];
for (int i = 1; i < 500; ++i)
{
q[i] = q[i - 1] + p[i];
}
int cnt = 500;
vector<Individual> res;
// 轮盘赌博
while (cnt--)
{
// 0-1的随机数
double r = rand() % N / (double)N;
// 使用二分查找 找到q中>=r的左边界
int l = 0, right = 499;
while (l < right)
{
int mid = (l + right) / 2;
if (q[mid] >= r)
{
right = mid;
}
else l = mid + 1;
}
// 向返回数组中插入选择的染色体
if (l >= 0 && l < 500) res.push_back(popu[l]);
else if (l < 0) res.push_back(popu[0]);
else if (l >= 500) res.push_back(popu[499]);
}
return res;
}
// main.cpp
#include "Genetic.h"
double f(Individual& x)
{
double x1 = x.code1.decode();
double x2 = x.code2.decode();
return 100 * (x1 * x1 - x2) * (x1 * x1 - x2) + (1 - x1) * (1 - x1);
}
int main()
{
probabilityinit();
// 500个个体的种群
vector<Individual> population(500);
thebest best;
// 获取随机生成的初始种群的最佳值
getbest(population, best);
// 跑500轮
int cnt = 500;
// 把(2.048, 2.048)单独拿出来
thebest execp(2.048, 2.048);
// 获取某一个点是2.048(编码表示不了的)的最小值
getexecpbest(execp);
cout << "遗传算法已经开始，初始解为:" << endl;
cout << "x1 = " << best.x1 << endl;
cout << "x2 = " << best.x2 << endl;
cout << "f(x1, x2) = " << best.val << endl;
while (cnt--)
{
// 1.获得当前种群适应度 以进行选择操作
population = select(population);
// 2.交叉操作 利用cross
for (int i = 0; i < 500; ++i)
{
for (int j = 0; j < i; ++j)
{
double r = rand() % N / (double)N;
if (r < Pc)
{
Cross(population[i], population[j]);
}
}
}
// 3.变异操作
for (int i = 0; i < 500; ++i)
{
double r = rand() % N / (double)N;
if (r < Pm)
{
int who = rand() % 2;
if (who == 0) population[i].code1.variation();
else population[i].code2.variation();
}
}
// 4.获得当前最优解
getbest(population, best);
int mytime = 500 - cnt;
if (mytime % 100 == 0)
{
cout << "不要着急，已经运行了" << mytime << "轮了" << endl;
}
}
// 如果例外情况更好 则更新best
if (best.val > execp.val)
{
best = execp;
}
cout << "500个个体的种群，进行500轮遗传算法，得到的最优解为" << endl;
cout << "x1 = " << best.x1 << endl;
cout << "x2 = " << best.x2 << endl;
cout << "f(x1, x2) = " << best.val << endl;
return 0;
}
三、运行结果与反思
我得到过的最好的运行结果是下图：
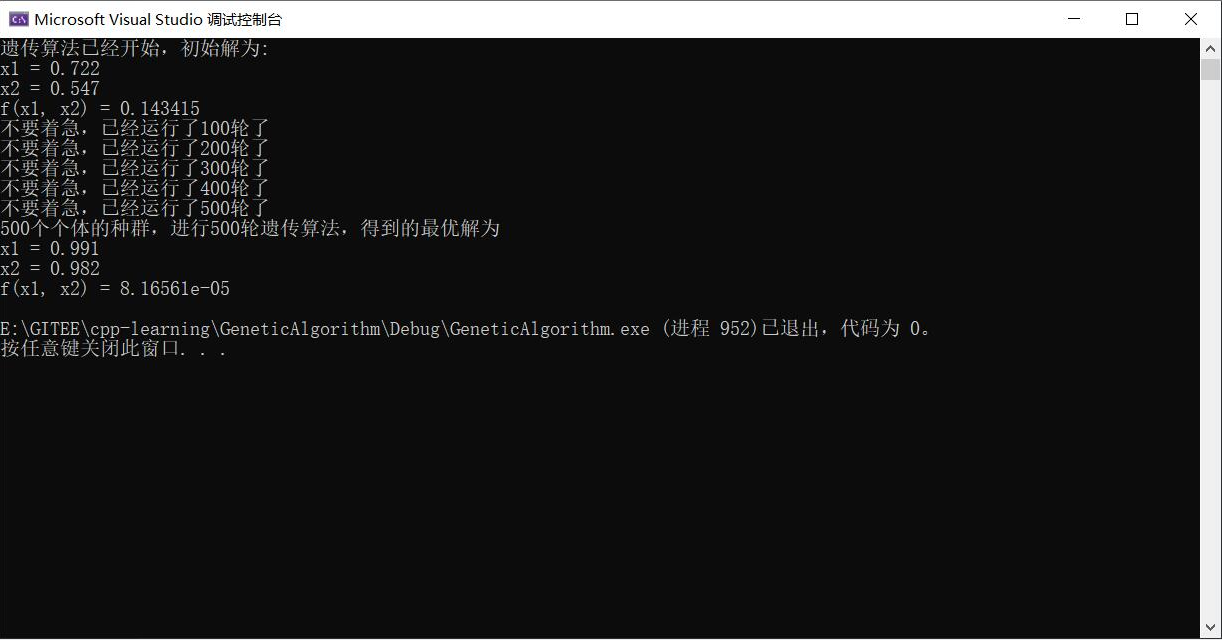
我们根据多元函数偏导数的知识，可以知道本题的最优解为
x1=1,x2=1,f(x1,x2)=0
x_1 = 1,x_2 = 1, f(x1, x2) = 0\\
x1=1,x2=1,f(x1,x2)=0
对应编码为1011 1110 1000, 1011 1110 1000，然而我并没有运行得到个解，并且这个遗传算法的解浮动比较大，下图是我随机一次运行：
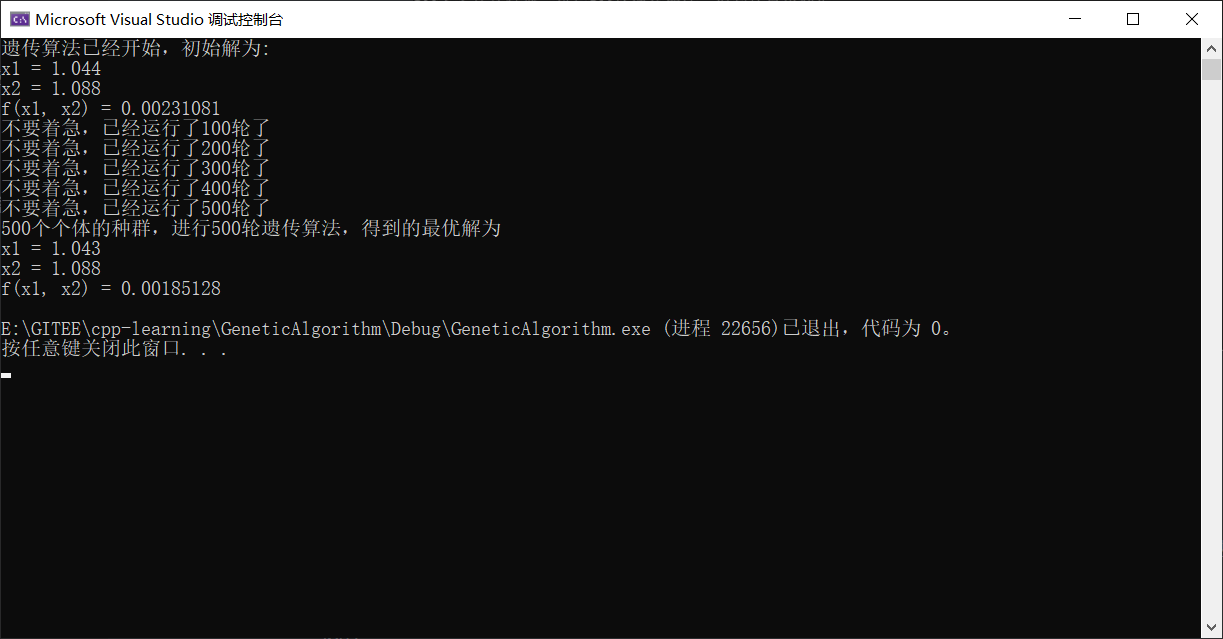
并且虽然我的程序是用C++编写的，但是可能因为我的设计原因，速度并不是很快（我没有参考别的遗传算法的代码设计，或许有什么巧妙的技巧我没有用到），大概500个种群运行500轮遗传算法需要的时间为3分钟左右。
猜测效果并不稳定且不好的一个原因是轮数不够多，因为我本人的电脑性能并没有GPU计算机好，所以我只运行了500轮，或许运行更多轮可以稳定的得到最优解。
另一个原因可能是我的交叉操作和变异操作都采用了最朴素的方法，并没有采用大家改进后的遗传算法，可能这也是效果不好的原因之一。
扫一扫
6万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
