青蛙跳台阶—递归思想的实现

原问题

  一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

  思路：既然青蛙一次可以跳上1个1级台阶或者一次跳上1个2级台阶，那么跳上一个n级台阶的方法：

• 要么是先跳上一个n-1级台阶然后再跳一个1级台阶做到；

• 要么是跳上一个n-2级台阶然后再跳上一个2级台阶实现;

所以跳上n级台阶的方法数等于跳上n-1级台阶的方法数加上跳上n-2级台阶的方法数，用f(n)表示跳上n级台阶的方法数,经过我们的分析，有
$$f(n)=f(n-1)+f(n-2)$$

$$f(1)=1$$

$$f(2)=2$$

  这不就是个斐波那契数列嘛，我们不妨用递归思想来实现这个计算。

#include <stdio.h>
long long Fib(int n)
{
	if (n == 2)
	{
		return 2;
	}
    else if(n==1)
    {
        return 1;
    }
	else
	{
		return Fib(n - 1) + Fib(n - 2);
	}
}
int main()
{
	int n;
	printf("请输入n的值\n");
	scanf("%d", &n);
	long long a = Fib(n);
	printf("%lld\n", a);
	return 0;
}

  但是实际运行发现，当n取到40左右的数字的时候，这个程序就需要运行好久的时间，这是为什么呢？原因是我们在做这个递归的时候进行了大量的重复计算。

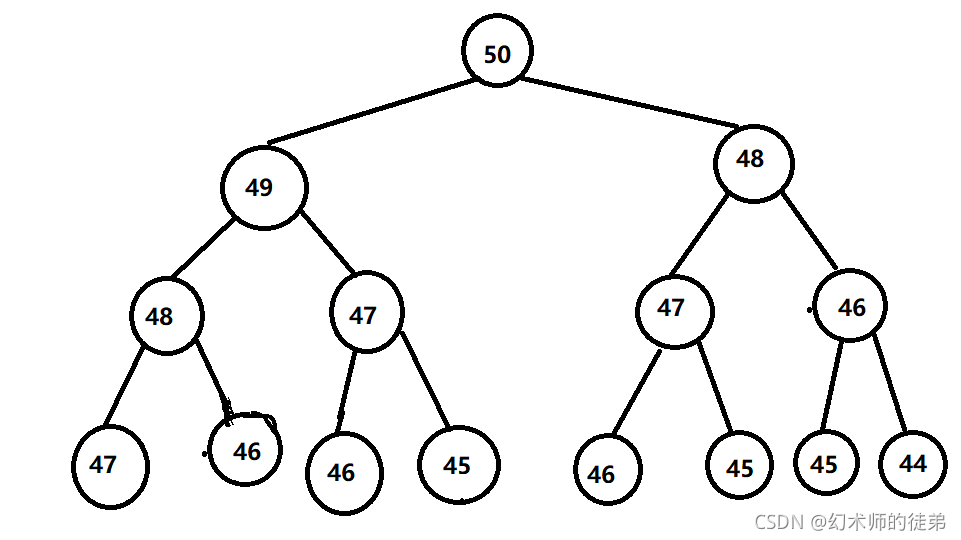
  可以看到，仅仅是进行到第3层，我们已经重复计算了4次f(46),3次f(47),3次f(45)，我们接着往下要运行完整个f(50)要进行不知道多少次的重复计算，很多重复计算都完全没有必要，既然我已经算出来了，为什么不直接调用还要再重复计算，浪费时间，因此，我们可以不用递归的思想来实现这个问题：

long long Fib(int n)
{
	int a = 1;
    int b = 2;
    int c = 3;
    if(n==1)
    {
        return a;
    }
    else if(n==2)
    {
        return b;
    }
    else
    {
        while(n>2)
        {
            c=a+b;
            a=b;
            b=c;
            n--;
        }
        return c;
    }
}


int main()
{
	int n;
	printf("请输入n的值\n");
	scanf("%d", &n);
	long long a = Fib(n);
	printf("%lld\n", a);
	return 0;
}

可以发现这次的运行速度明显快了很多。

变种1

  一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

思路1：和上面问题的分析思路类似，既然要跳n级台阶，我们一共有n种完成方法：

• 一次跳n-1级，然后跳1级
• 一次跳n-2级，然后跳2级
• …
• 一次跳1级，然后跳n-1级
• 直接跳n级

  所以跳n级台阶的方法数等于跳n-1级台阶的方法数加跳n-2级台阶的方法数加…加跳一级台阶的方法数+直接跳n级(方法数是1)

  同样以f(n)代表跳n级台阶的方法数，根据我们上面的分析，有：
$$f(n)=f(n-1)+f(n-2)+...+f(1)+1$$
求解这个数列的通项公式，我们不妨在写一下f(n-1)的表达式
$$f(n-1)=f(n-2)+...+f(1)+1$$
两式作差
$$f(n)-f(n-1)=f(n-1)$$

$$f(n)=2f(n-1)$$

$$f(n)是一个等差数列，公差为2，首项f(1)=1$$

$$f(n)=2^{n-1}$$

思路2. 因为我们可以一次直接跳1~n级台阶，所以不管是什么方法，要到达n级台阶，n级台阶必须要站上去，其他的台阶都可以选择站上去或者不站上去，因此总共有2^(n-1)种可能。

这个问题我们可以直接用pow函数求解，当然也可以用递归实现

//递归

unsigned long long frog(int n)
{
	if (n > 1)
	{
		return 2 * frog(n - 1);
	}
	else
	{
		return 1;
	}
}

int main()
{
	int n;
	printf("请输入n的值\n");
	scanf("%d", &n);
	unsigned long long a = frog(n);
	printf("%llu\n", a);
	return 0;
}

//pow函数

#include <stdio.h>
#include <math.h>

int main()
{
	int n;
	printf("请输入n的值\n");
	scanf("%d", &n);
	unsigned long long b = (unsigned long long)pow(2, n - 1);
	printf("%llu\n", b);
	return 0;
}

变种2

  一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上m级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

  这个问题显然是要分类讨论的，因为我们不知道n和m的大小关系。

① n<=m

  这个情况显然是简单的，因为青蛙可以一次跳上m级由于m>=n青蛙也一定可以一次跳上n级，我们可以把这种情况转化为变种1的问题
$$f(n)=2f(n-1)$$

$$f(n)=2^{n-1}$$

② n>m

  这个情况下，我们不能一次跳到n级，要跳上n级，

• 要么跳上n-1级然后再跳上1级；
• 要么跳上n-2级然后再跳上2级；
• …
• 要么跳上n-m级然后再跳上m级；

注意：往下就没有情况了，因为我们每次罗列的跳上n级的方法都是后面的动作是1步可以完成的，我们的青蛙并不能一次跳m+1级

  所以一次跳n级的方法数等于一次跳n-1级的方法数加一次跳n-2级的方法数加一次跳n-3级的方法数加…加一次跳n-m级的方法数。

  以f(n)作为跳n级的方法数，经过我们的分析，有
$$f(n)=f(n-1)+...+f(n-m)$$
  我们要能用递归来处理的话，递归式子算数因子个数不能在自动变化，因此我们再化简一下上式
$$f(n-1)=f(n-2)+...f(n-1-m)$$
两式作差
$$f(n)-f(n-1)=f(n-1)-f(n-1-m)$$

$$f(n)=2f(n-1)-f(n-1-m)$$

我们用c语言实现如下：

#include <stdio.h>

int frog(int n, int m)
{
	if (n > m)
	{
		return 2 * frog(n - 1, m) - frog(n - 1 - m, m);
	}
	else
	{
		if (n <= 1)
		{
			return 1;
		}
		return 2 * frog(n - 1,m);
	}
}

int main()
{
	int m, n;
	printf("请输入m和n 以m n的形式输入\n");
	scanf("%d %d", &m, &n);
	int b=frog(n,m);
	printf("%d", b);
	return 0;
}

1, m) - frog(n - 1 - m, m);
}
else
{
if (n <= 1)
{
return 1;
}
return 2 * frog(n - 1,m);
}
}

int main()
{
int m, n;
printf(“请输入m和n 以m n的形式输入\n”);
scanf("%d %d", &m, &n);
int b=frog(n,m);
printf("%d", b);
return 0;
}