详解青蛙跳台阶问题（递归和迭代）

---

一、青蛙跳台阶问题

一只青蛙一次最少可以跳一次台阶，一次最多可以跳两次台阶，问：当这只青蛙如果要跳上n阶台阶有几种跳法？

二、解题思路

我们设台阶数为n;
当n = 1时，有一种跳法，直接跳一层跳上去；
当n = 2时，有两种跳法，可以一次跳两层；或者一次跳一层，一次跳一层；
当n = 3时，有三种跳法，可以一层一层地往上跳；可以跳一层，再跳两层；可以先跳两层，再跳一层；
当n = 4时，有五种跳法，可以一层一层地往上跳；可以两层两层跳；可以先跳两层再一层一层的跳；可以先一层一层跳，最后直接跳两层；可以先跳一层，再跳两层，再跳一层；
…

以此类推，我们不难分析
n层的跳法 = (n-2)层跳法+(n-1)层跳法

如果还感觉不是很清晰，我们可以画图尝试理解

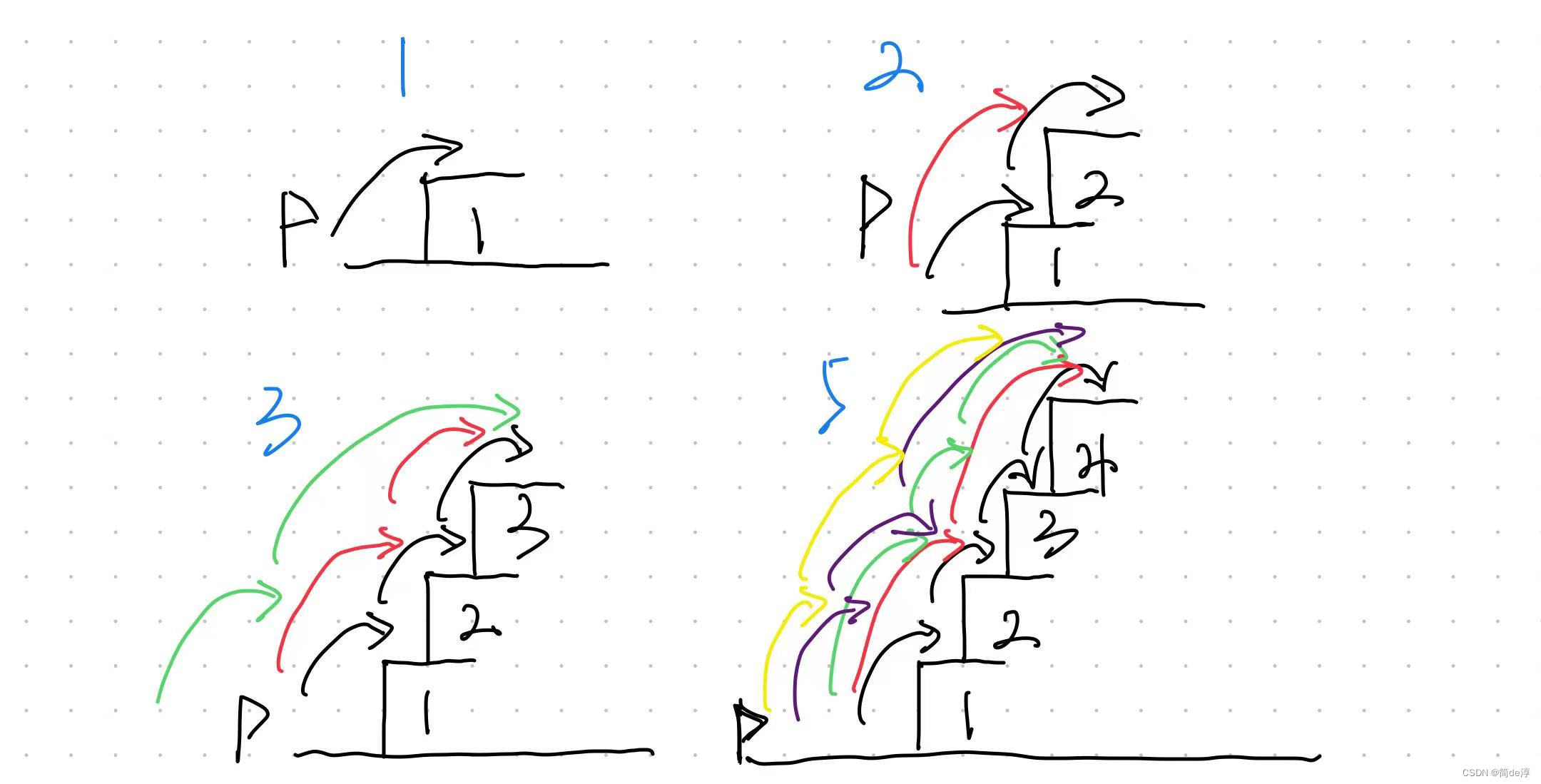
1，2，3，5，8，13…我们可以得出以上的数列，我们可以从中发现规律，这不就是斐波那契数列嘛吗，第三数等于前两数相加

代码实现

1.递归法

#include"stdio.h"
int taijie(n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	while (n >= 2)//1的时候不适用
	{
		c = a + b;
		a = b;//把原来的第二个数变成新计算中的第一个数
		b = c;//把算出的结果变为新计算的第二个数
		n--;
	}
	return c;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = taijie(n);
	printf("%d", ret);
	return 0;
}

2. 迭代法

#include<stdio.h>
int taijie(int m)
{
    int ret = 0;
    if (m <= 1)
    {
        ret = 1;//第一项为1
    }
    else
    {
        ret = taijie(m - 1) + taijie(m - 2);//一项以后，后一项等于前两项的和
    }
    return ret;
}
int main()
{
    int n = 0;
    scanf("%d", &n);
    printf("%d", taijie(n));
    return 0;
}

这里说明下，在使用递归的时候会发现其中的taijie（）会在调用过程中出现很多的重复，再n比较小的时候我们看不出区别，但是在n值比较大的时候仍然使用递归的方式就会出现运算较慢的情况，所以在n值比较大的情况下，迭代就很提高运算的效率

---

总结

以上就是对于青蛙问题的详细解析了，感觉不错的话可以点下关注哦，有什么问题也可以在评论区留言哦，我会及时回答的。