算法学习笔记：28.前缀树——从原理到实战，涵盖 LeetCode 与考研 408 例题

前缀树（Trie，又称字典树或单词查找树）是一种专为字符串处理设计的树形数据结构，由 Edward Fredkin 于 1960 年提出。它通过共享字符串的前缀来高效存储和检索字符串集合，在 autocomplete（自动补全）、拼写检查、IP 路由等场景中有着广泛应用。

前缀树的基本概念与结构

定义与特点

前缀树是一种多叉树，每个节点代表一个字符串的前缀，其特点如下：

节点结构：每个节点包含一个布尔值isEnd（标记该节点是否为某个字符串的结尾）和若干个子节点（通常对应 26 个英文字母，也可扩展到其他字符）。

根节点：为空节点，不存储任何字符，是所有字符串的起点。

前缀共享：具有相同前缀的字符串会共享前缀部分的节点，显著减少存储空间。

高效操作：插入、查找、前缀匹配的时间复杂度均为O(L)，其中L是字符串的长度，与字符串总数无关。

结构图示

以下是存储字符串 "apple"、"app"、"banana" 的前缀树结构：

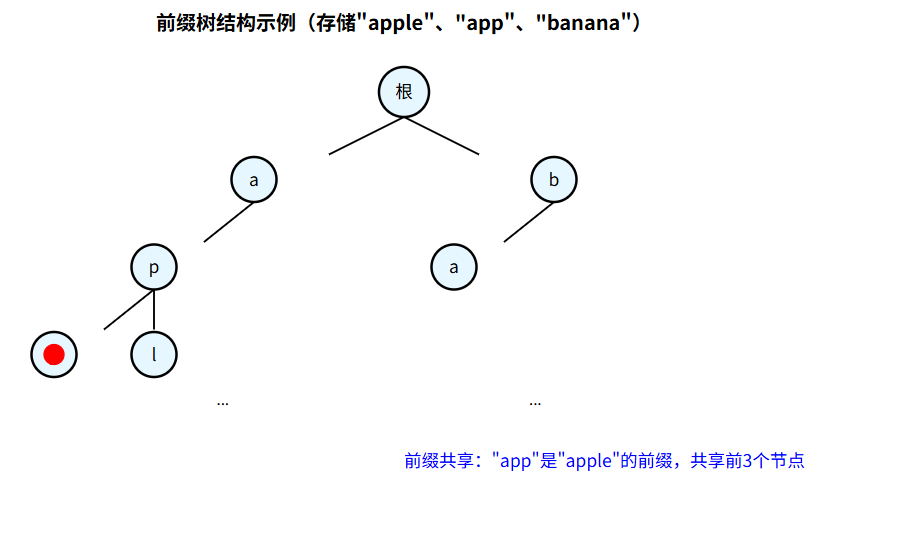
`前缀树的核心操作`

`插入操作`

思路：从根节点开始，逐个字符处理字符串：

1. 对于当前字符，若节点的子节点中不存在该字符，则创建新节点。

2. 移动到对应子节点，继续处理下一个字符。

3. 字符串处理完毕后，将最后一个节点标记为结尾（`isEnd = true`）。

Java 代码：

class TrieNode {

    public TrieNode[] children; // 子节点（假设只包含小写字母）

    public boolean isEnd; // 是否为单词结尾

    public TrieNode() {

        children = new TrieNode[26]; // 26个小写字母

        isEnd = false;

    }

}

public class Trie {

    private TrieNode root;

    public Trie() {

        root = new TrieNode(); // 根节点为空

    }

// 插入字符串

    public void insert(String word) {

        TrieNode node = root;

        for (int i = 0; i < word.length(); i++) {

            char c = word.charAt(i);

            int index = c - 'a'; // 计算字符索引（0-25）

            if (node.children[index] == null) {

                node.children[index] = new TrieNode(); // 新建节点

            }

            node = node.children[index]; // 移动到子节点

        }

        node.isEnd = true; // 标记单词结尾

    }

}

查找操作

思路：从根节点开始遍历字符串的每个字符：

若当前字符的子节点不存在，返回false。

移动到对应子节点，继续处理下一个字符。

字符串处理完毕后，返回最后一个节点的isEnd（确保是完整单词）。

Java 代码：

// 查找字符串是否存在于前缀树中

public boolean search(String word) {

    TrieNode node = root;

    for (int i =