算法学习笔记：27.堆排序（生日限定版）——从原理到实战，涵盖 LeetCode 与考研 408 例题

堆排序（Heap Sort）是一种基于二叉堆数据结构的高效排序算法，由计算机科学家 J. W. J. Williams 于 1964 年提出。它结合了选择排序的思想和二叉堆的特性，具有时间复杂度稳定（O (nlogn)）、原地排序（空间复杂度 O (1)） 等优点，在大规模数据排序场景中应用广泛。

堆的基本概念与性质 🎂

二叉堆的定义​

二叉堆是一种完全二叉树（除最后一层外，每层节点均满，最后一层节点靠左排列），分为两种类型：​

最大堆：每个父节点的值大于等于其左右子节点的值（parent.val ≥ left.val 且 parent.val ≥ right.val）。​
最小堆：每个父节点的值小于等于其左右子节点的值（parent.val ≤ left.val 且 parent.val ≤ right.val）。​ 堆排序中通常使用最大堆，本文以最大堆为例讲解。

​

堆的存储结构 🎂

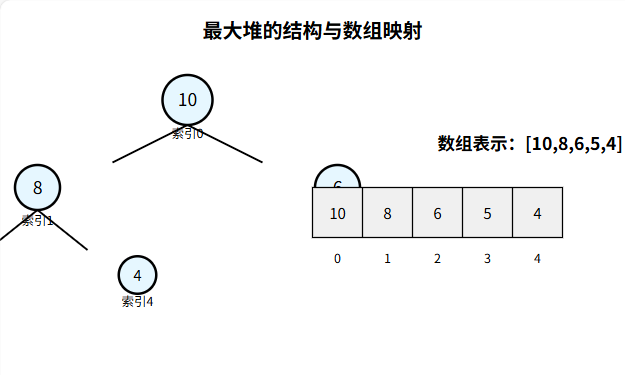
堆通常用数组实现，利用完全二叉树的性质映射节点索引（假设数组索引从 0 开始）：​

对于节点 i：​
左子节点索引：2i + 1
​右子节点索引：2i + 2​
父节点索引：(i - 1) / 2（整数除法）

构建最大堆​

构建最大堆需从最后一个非叶子节点开始，依次向前执行堆调整操作。最后一个非叶子节点的索引为 (n / 2) - 1（n 为数组长度）。

构建过程代码：

private void buildMaxHeap(int[] arr) {
    int n = arr.length;
    // 从最后一个非叶子节点开始调整
    for (int i = (n / 2) - 1; i >= 0; i--) {
        maxHeapify(arr, n, i);
    }
}

堆排序完整实现​ 🎂

算法流程​

调用 buildMaxHeap 将数组转为最大堆。​
初始化堆大小 heapSize = n。​
循环 n - 1 次：​
交换堆顶（arr[0]）与堆尾（arr[heapSize - 1]）元素。​
减小堆大小（heapSize–）。​
调用 maxHeapify 调整堆顶元素，维护剩余元素的堆性质。

堆排序图示

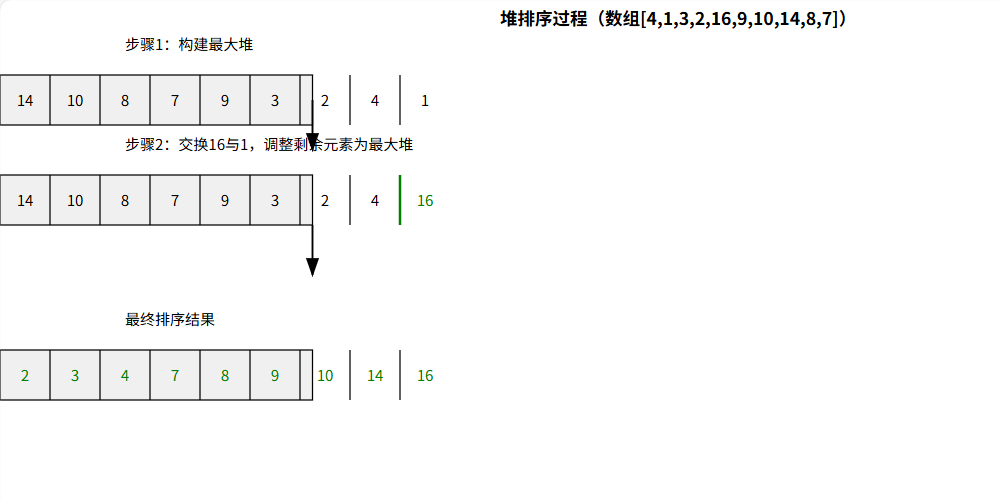
程序代码：

public class HeapSort {
    public void sort(int[] arr) {
        int n = arr.length;
        if (n <= 1) return;

        // 步骤1：构建最大堆
        buildMaxHeap(arr);

        // 步骤2：排序阶段
        int heapSize = n;
        for (int i = n - 1; i > 0; i--) {
            // 交换堆顶与当前堆尾
            swap(arr, 0, i);
            heapSize--; // 堆大小减1
            // 调整剩余元素为最大堆
            maxHeapify(arr, heapSize, 0);
        }
    }

    private void buildMaxHeap(int[] arr) {
        int n = arr.length;
        for (int i = (n / 2) - 1; i >= 0; i--) {
            maxHeapify(arr, n, i);
        }
    }

    private void maxHeapify(int[] arr, int heapSize, int i) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int maxIndex = i;

        if (left < heapSize && arr[left] > arr[maxIndex]) {
            maxIndex = left;
        }
        if (right < heapSize && arr[right] > arr[maxIndex]) {
            maxIndex = right;
        }

        if (maxIndex != i) {
            swap(arr, i, maxIndex);
            maxHeapify(arr, heapSize, maxIndex);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] arr = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
        HeapSort heapSort = new HeapSort();
        heapSort.sort(arr);
        System.out.println(Arrays.toString(arr)); // 输出：[1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
    }
}

复杂度分析​

时间复杂度：​
构建最大堆：O (n)（严格证明需用到堆的高度求和，结果为 O (n)）。​
排序阶段：共执行 n-1 次堆调整，每次调整为 O (logn)，总时间 O (nlogn)。​
整体时间复杂度：O (nlogn)，且最坏情况下仍为 O (nlogn)，稳定性优于快速排序。​
空间复杂度：O (1)，原地排序，仅需常数级额外空间。

LeetCode 例题实战​ 🎂

例题 1：912. 排序数组（中等）​

题目描述：给你一个整数数组 nums，请你将该数组升序排列。

​
示例：
输入：nums = [5,2,3,1]​
输出：[1,2,3,5]

代码实现

class Solution {
    public int[] sortArray(int[] nums) {
        if (nums == null || nums.length <= 1) {
            return nums;
        }
        heapSort(nums);
        return nums;
    }

    private void heapSort(int[] arr) {
        int n = arr.length;
        // 构建最大堆
        for (int i = (n / 2) - 1; i >= 0; i--) {
            maxHeapify(arr, n, i);
        }
        // 排序阶段
        for (int i = n - 1; i > 0; i--) {
            swap(arr, 0, i);
            maxHeapify(arr, i, 0);
        }
    }

    private void maxHeapify(int[] arr, int heapSize, int i) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int maxIndex = i;
        if (left < heapSize && arr[left] > arr[maxIndex]) {
            maxIndex = left;
        }
        if (right < heapSize && arr[right] > arr[maxIndex]) {
            maxIndex = right;
        }
        if (maxIndex != i) {
            swap(arr, i, maxIndex);
            maxHeapify(arr, heapSize, maxIndex);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

例题 2：215. 数组中的第 K 个最大元素（中等）​

题目描述：给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。​

示例：
输入: [3,2,1,5,6,4] 和 k = 2​
输出: 5

解题思路​

利用最大堆的堆顶为最大值的特性，弹出k-1个最大值后，堆顶即为第 k 个最大元素。或使用最小堆（更高效），维护大小为 k 的最小堆，堆顶为第 k 个最大元素。
方法 2（最小堆）Java 代码

class Solution {
    public int findKthLargest(int[] nums, int k) {
        // 最小堆，堆顶为第k大元素
        PriorityQueue<Integer> minHeap = new PriorityQueue<>(k);
        for (int num : nums) {
            if (minHeap.size() < k) {
                minHeap.add(num); // 堆未满，直接加入
            } else if (num > minHeap.peek()) {
                // 元素大于堆顶，替换堆顶并调整
                minHeap.poll();
                minHeap.add(num);
            }
        }
        return minHeap.peek(); // 堆顶为第k大元素
    }
}

复杂度分析​
时间复杂度：O (nlogk)，插入 n 个元素，每次堆调整为 O (logk)。​
空间复杂度：O (k)，堆存储 k 个元素。
​

考研 408 例题解析​ 🎂

例题 1：概念辨析题（选择题）​

题目：下列关于堆的叙述中，正确的是（ ）。
​A. 最大堆中，从根节点到任意叶子节点的路径上的元素是递减的​
B. 堆排序是稳定的排序算法​
C. 构建最大堆的时间复杂度为 O (nlogn)​
D. 堆的调整操作（Heapify）的时间复杂度为 O (n)​

答案：A​
解析：​
A 正确：最大堆中，父节点的值大于等于子节点，因此根到叶子的路径元素递减。​
B 错误：堆排序中交换元素可能改变相等元素的相对顺序（如 [2,2] 排序后可能颠倒），因此不稳定。​
C 错误：构建最大堆的时间复杂度为 O (n)，而非 O (nlogn)。​
D 错误：堆的调整操作时间复杂度为 O (logn)，与树的高度相关。​

例题 2：算法设计题（408 高频考点）​

题目：设计一个算法，利用堆实现一个优先级队列，支持插入元素和提取最大元素操作，并分析两种操作的时间复杂度。​

解题思路​
优先级队列结构：用数组存储堆，维护最大堆性质。​
插入操作：​
将新元素添加到堆尾。​
执行 “上浮” 操作：与父节点比较，若大于父节点则交换，直至根节点或小于父节点。​
提取最大元素操作：​
取出堆顶元素（最大值）。​
将堆尾元素移至堆顶。​
执行 “下沉” 操作（即堆调整），维护最大堆性质。

Java 代码实现

public class MaxPriorityQueue {
    private int[] heap;
    private int size; // 当前元素个数
    private int capacity; // 队列容量

    public MaxPriorityQueue(int capacity) {
        this.capacity = capacity;
        heap = new int[capacity + 1]; // 1-based索引，便于计算子节点
        size = 0;
    }

    // 插入元素
    public void insert(int val) {
        if (size == capacity) {
            throw new IllegalStateException("队列已满");
        }
        size++;
        heap[size] = val;
        swim(size); // 上浮调整
    }

    // 提取最大元素
    public int extractMax() {
        if (size == 0) {
            throw new NoSuchElementException("队列为空");
        }
        int max = heap[1];
        swap(1, size); // 交换堆顶与堆尾
        size--;
        sink(1); // 下沉调整
        return max;
    }

    // 上浮操作（用于插入）
    private void swim(int k) {
        while (k > 1 && heap[k] > heap[k / 2]) { // 与父节点比较
            swap(k, k / 2);
            k = k / 2;
        }
    }

    // 下沉操作（用于提取最大元素）
    private void sink(int k) {
        while (2 * k <= size) { // 存在左子节点
            int j = 2 * k; // 左子节点
            if (j < size && heap[j] < heap[j + 1]) { // 右子节点更大
                j++;
            }
            if (heap[k] >= heap[j]) {
                break; // 已满足最大堆性质
            }
            swap(k, j);
            k = j;
        }
    }

    private void swap(int i, int j) {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }
}

复杂度分析​

插入操作：时间复杂度 O (logn)，上浮操作最多执行 logn 次（树的高度）。​
提取最大元素：时间复杂度 O (logn)，下沉操作最多执行 logn 次。​

堆排序的扩展与应用​ 🎂

实际应用场景​

优先级队列：操作系统的进程调度、任务队列等，需频繁获取最大值 / 最小值。​
Top-K 问题：如获取海量数据中前 k 个最大元素（如 LeetCode 215 题）。​
流数据处理：实时处理数据流，维护动态数据的 Top-K 元素。​
堆排序：适用于大规模数据排序，尤其是内存有限的场景（原地排序）。​

与其他排序算法的对比

排序算法	平均时间复杂度	最坏时间复杂度	空间复杂度
堆排序	O(nlogn)	O(nlogn)	O(1)
快速排序	O(nlogn)	O(n²)	O(logn)
归并排序	O(nlogn)	O(nlogn)	O(n)

考研 408 备考要点​ 🎂

核心考点：堆的性质、堆的构建与调整、堆排序的步骤与复杂度。​

重点掌握：​

堆的索引计算（父节点与子节点的关系）。​
堆调整（Heapify）的递归与非递归实现。​
堆排序与优先级队列的关联，以及 Top-K 问题的解法。​

常见错误：​

混淆最大堆与最小堆的调整逻辑。​
构建堆时从 0 开始而非最后一个非叶子节点。​
忽略堆排序的不稳定性，错误认为其稳定。​

总结​ 🎂

堆排序作为一种高效的排序算法，凭借 O (nlogn) 的稳定时间复杂度和原地排序的特性，在大规模数据处理中有着不可替代的地位。本文从堆的基本概念出发，详细讲解了堆的构建、调整操作和堆排序的完整流程，结合 LeetCode 例题（排序数组、Top-K 问题）展示了堆的核心应用，通过考研 408 例题解析了概念辨析和算法设计思路，并穿插 SVG 图示直观呈现了堆的结构与操作过程。​
掌握堆排序的关键在于：​
深刻理解堆的性质及索引映射关系。​
熟练实现堆的调整（Heapify）、构建和排序过程。​
灵活运用堆解决优先级队列、Top-K 等实际问题。​
在考研备考中，堆的性质、堆排序的复杂度分析以及优先级队列的实现是重点，需结合具体例题深入练习，理解堆在数据结构中的核心作用。