算法学习笔记：29.拓扑排序——从原理到实战，涵盖 LeetCode 与考研 408 例题

拓扑排序（Topological Sorting）是一种针对有向无环图（DAG）的线性排序算法，它将图中的顶点按照一定规则排列，使得对于图中的任意一条有向边 u→v，顶点 u 都排在顶点 v 之前。拓扑排序在任务调度、课程安排、编译依赖等场景中有着广泛应用。

---

拓扑排序的基本概念与适用场景

核心定义

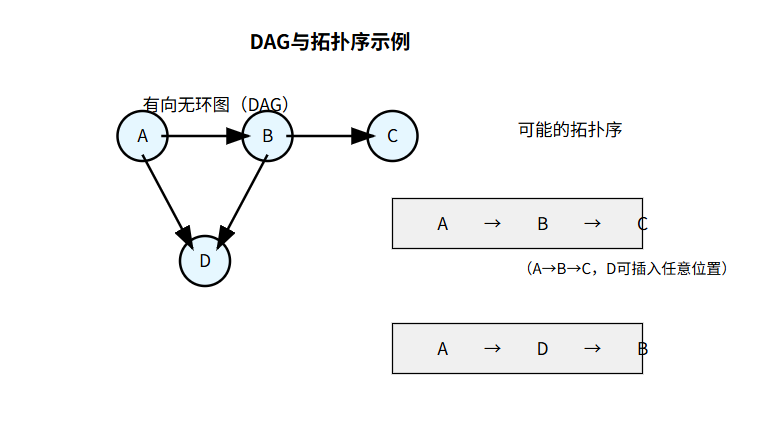
• 有向无环图（DAG）：顶点间的边有方向，且不存在环路的图。拓扑排序仅适用于 DAG，若图中存在环，则不存在拓扑排序。

• 拓扑序：对于 DAG 中的顶点，存在一个线性序列 v₁, v₂, ..., vₙ，使得所有有向边 vᵢ→vⱼ 均满足 i < j。一个 DAG 可能存在多个拓扑序。

应用场景

• 任务调度：若任务 B 依赖任务 A，则 A 必须在 B 之前执行，拓扑排序可确定任务执行顺序。

• 课程安排：大学课程存在先修关系（如 “数据结构” 需先修 “C 语言”），拓扑排序可生成合理的选课顺序。

• 编译依赖：编译器处理源文件时，需按依赖关系（如头文件包含）确定编译顺序。

DAG 与拓扑序示例

拓扑排序的核心算法

Kahn算法（基于入度与队列）

核心思想：通过维护节点的入度（指向该节点的边数），逐步选出入度为0的节点（无前置依赖），并减少其邻接节点的入度，直至所有节点被处理或检测到环。

算法步骤

1. 计算入度：遍历图，记录每个节点的入度。

2. 初始化队列：将所有入度为0的节点加入队列。

3. 生成拓扑序：

- 出队一个节点，加入拓扑序。

- 对该节点的所有邻接节点，入度减1；若入度变为0，入队。

4. 检测环：若拓扑序长度小于节点总数，则图中存在环，无拓扑序。

基于DFS的拓扑排序

核心思想：通过深度优先搜索，在回溯时将节点加入拓扑序（逆后序遍历），若搜索中遇到回边（指向已访问但未回溯的节点），则存在环。

算法步骤：

1. 标记访问状态：用三个状态标记节点：未访问（0）、访问中（1）、已访问（2）。

2. 递归DFS：

- 若节点状态为访问中，检测到环。

- 若节点未访问，标记为访问中，递归遍历所有邻接节点。

- 回溯时，标记节点为已访问，加入拓扑序。

3. 逆序输出：拓扑序为逆后序遍历结果。

LeetCode例题实战

例题1：207. 课程表（中等）