算法学习笔记：25.回溯算法之迷宫寻路——从原理到实战，涵盖 LeetCode 与考研 408 例题

迷宫寻路是回溯算法的经典应用场景，其核心是在复杂路径中通过 “尝试 - 回溯” 探索所有可能的路径，最终找到通往终点的解。无论是在算法竞赛（如 LeetCode）还是考研计算机专业基础综合（408）中，迷宫寻路问题及其变种都是考察回溯思想的高频考点。

---

迷宫寻路的回溯算法思路

问题定义

迷宫通常被抽象为一个二维网格，其中：

• 0 表示可通行的空地。

• 1 表示不可通行的墙壁。

• 起点 (startX, startY) 和终点 (endX, endY) 是网格中的两个特殊位置。

问题目标：从起点出发，通过上下左右四个方向移动，找到一条到达终点的路径（或所有路径），移动过程中不能穿过墙壁，也不能重复经过同一位置。

回溯算法核心思路

回溯算法通过递归探索所有可能的路径，若当前路径无法到达终点，则回溯到上一步，尝试其他方向。具体步骤如下：

1. 标记当前位置：到达某位置 (x, y) 后，标记该位置为 “已访问”（避免重复进入）。
2. 判断终点：若 (x, y) 是终点，则记录当前路径（若需所有路径）或直接返回成功。
3. 尝试方向：依次尝试上、下、左、右四个方向：

• • 若方向未越界、不是墙壁、未被访问，则递归探索该方向。

• • 若递归返回成功（找到终点），则继续回溯或返回；若失败，则尝试下一个方向。
  • 回溯清理：若所有方向均无法到达终点，取消当前位置的 “已访问” 标记，返回上一步。

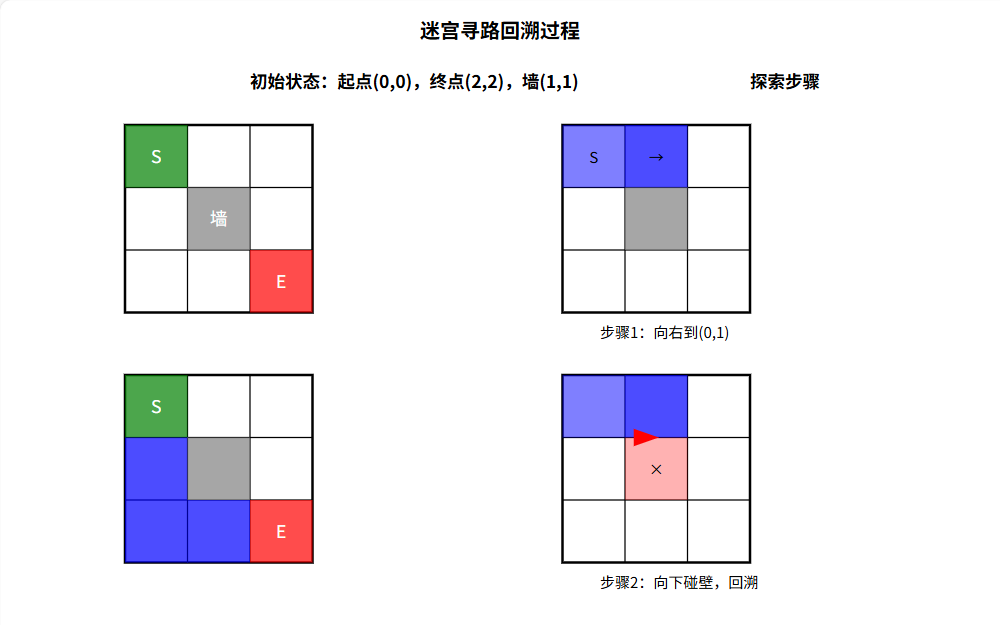
算法流程图示

（以 3×3 迷宫为例）

LeetCode例题实战

例题1：490. 迷宫（中等）

题目描述：由空地（0）和墙（1）组成的迷宫中有一个球。球可以向上下左右四个方向滚动，但在遇到墙之前不会停止滚动。当球停下时，可以选择下一个方向。给定球的起始位置、目的地和迷宫，判断球能否在目的地停下。

示例：

输入：

迷宫：[[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]]

起始位置：[0,4]

目的地：[4,4]

输出：true

解释：球可以滚动到目的地（路径：右→下→左→下→右）

解题思路

1. **与传统迷宫的区别**：球会“滚动”直到撞墙才停下，而非一步一格移动。

2. **回溯思路**：

- 从起点出发，尝试四个方向滚动，记录停下的位置（撞墙前的最后一个空地）。

- 若停下的位置是终点，返回true。

- 若该位置已访问过，跳过（避免循环）。

- 否则标记为已访问，递归探索从该位置出发的四个方向。

- 回溯时无需取消标记（因滚动路径唯一，不会重复访问）。

代码实现

class Solution {

    private int[][] directions = {
  
  {-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // 上、下、左、右

    private int rows, cols;

    private boolean[][] visited;