算法学习笔记：24.回溯算法之八皇后问题 ——从原理到实战，涵盖 LeetCode 与考研 408 例题

八皇后问题是回溯算法的经典案例，由国际象棋棋手马克斯・贝瑟尔于 1848 年提出。问题要求在 8×8 的棋盘上放置 8 个皇后，使它们不能互相攻击（即任意两个皇后不能处于同一行、同一列或同一斜线上）。作为回溯算法的标杆问题，八皇后不仅是 LeetCode 的高频考题，也是考研计算机专业基础综合（408）的重点考察内容。

---

八皇后问题核心思路

问题定义与约束

在n×n的棋盘上放置n个皇后，满足以下约束：

• 任意两个皇后不在同一行。

• 任意两个皇后不在同一列。

• 任意两个皇后不在同一斜线上（包括主对角线和副对角线）。

以 8 皇后为例，其解共有 92 种，每种解对应皇后在棋盘上的一种合法布局。

 回溯算法思路

回溯算法的核心是 “尝试 - 检测 - 回溯”：通过递归尝试放置皇后，若违反约束则回溯到上一步，调整位置后继续尝试，直至找到所有合法解。具体步骤如下：

1. 按行放置：由于皇后不能在同一行，可按行依次放置（第i个皇后放在第i行），只需考虑列和对角线约束。

1. 列冲突检测：记录已放置皇后的列索引，若当前列已被占用则冲突。

1. 对角线冲突检测：对于第i行第j列的皇后，与第k行第l列的皇后，若|i - k| == |j - l|则在同一斜线，冲突。

1. 递归回溯：

• • 若已放置n个皇后（到达最后一行），记录当前解。

• • 否则，对当前行的每一列尝试放置皇后：

• • • 若不冲突，标记列和对角线为占用，递归处理下一行。

• • • 递归返回后，撤销标记（回溯），尝试下一列。

算法流程图

（以 4 皇后为例，展示部分过程）

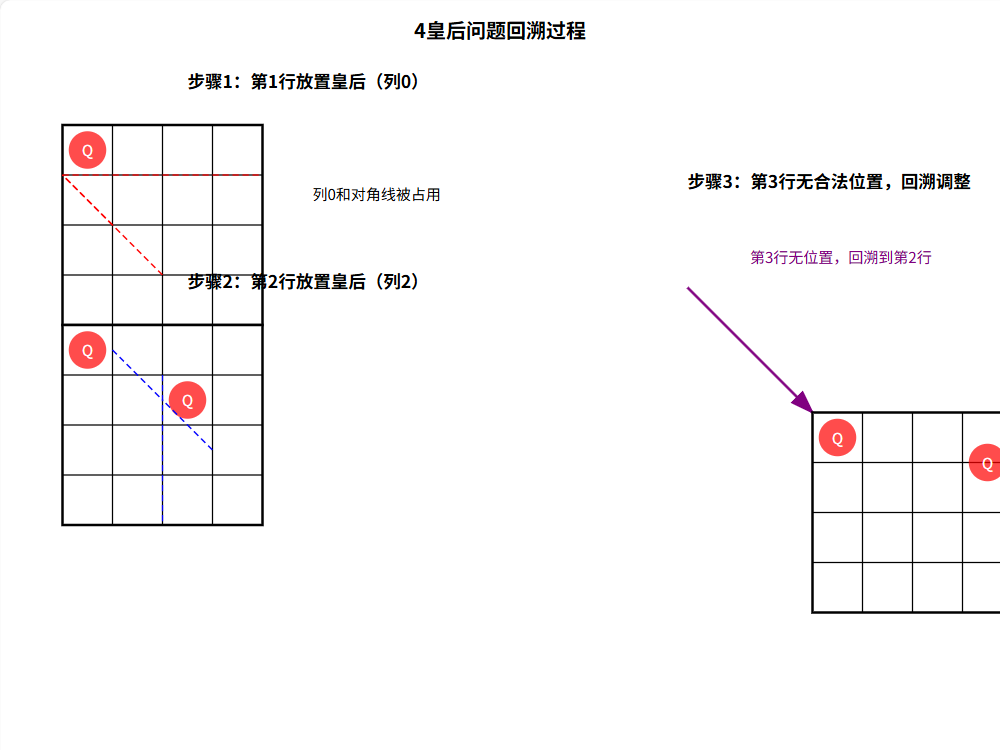
LeetCode例题实战

例题1：51. N 皇后（困难）

题目描述：按照国际象棋的规则，摆放`n`个皇后，使它们不能相互攻击。给你一个整数`n`，返回所有不同的`n`皇后问题的解决方案。每个解决方案包含一个不同的`n`皇后问题的棋子放置方案，该方案中`'Q'`和`'.'`分别代表皇后和空位。

示例：

输入：n = 4

输出：[[".Q..","...Q","Q...","..Q."],

["..Q.","Q...","...Q",".Q.."]]

解题思路

- `board`：二维数组表示棋盘，记录皇后位置。

- `columns`：哈希集记录已占用的列。

- `diagonals1`：哈希集记录已占用的主对角线（`行-列`为定值）。

- `diagonals2`：哈希