洛谷 P3807 【模板】卢卡斯定理

最新推荐文章于 2024-08-24 20:22:57 发布

原创最新推荐文章于 2024-08-24 20:22:57 发布 · 281 阅读

0 ·

CC 4.0 BY-SA版权

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

这篇博客介绍了洛谷P3807题目的解题思路，重点讲解了卢卡斯定理在算法分析中的应用，并提供了AC代码。文章强调在解决此类问题时，正确使用long long数据类型的重要性。

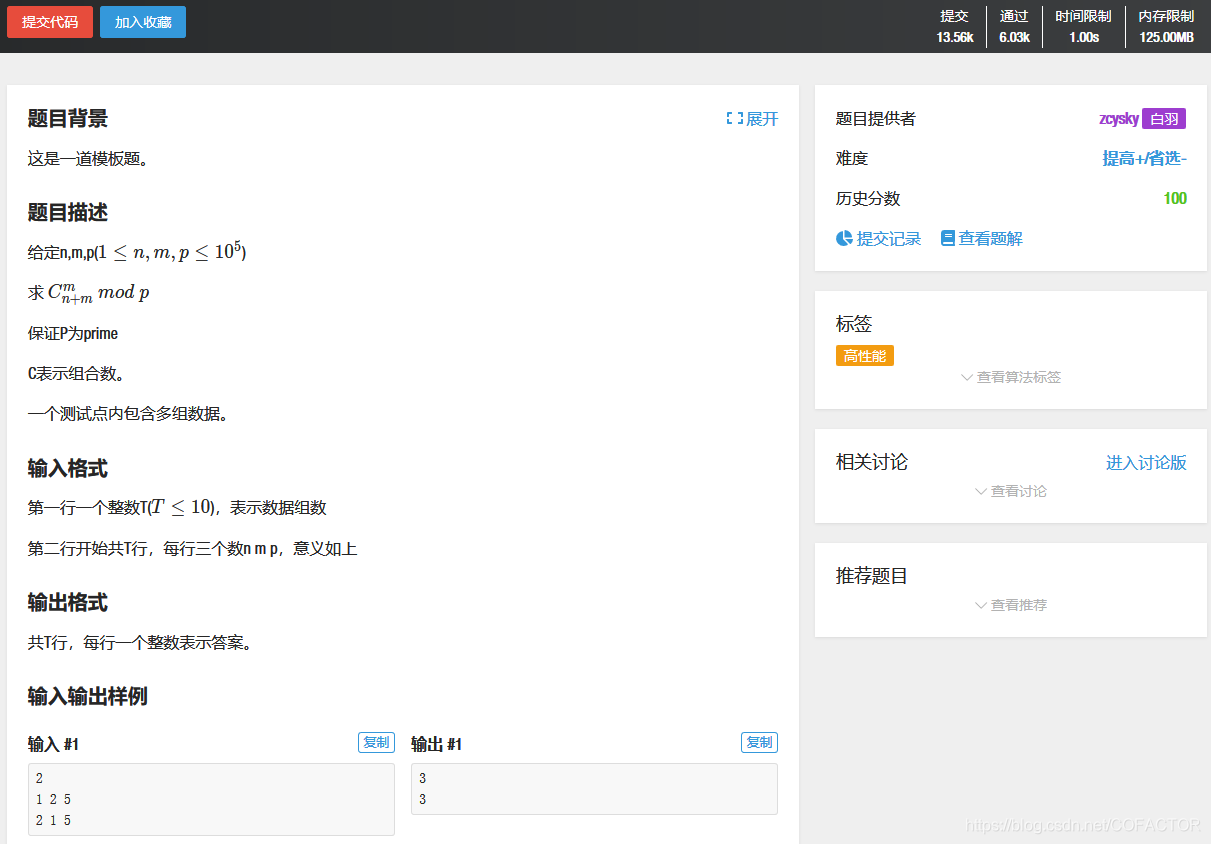
一、题目描述

在这里插入图片描述

二、算法分析说明

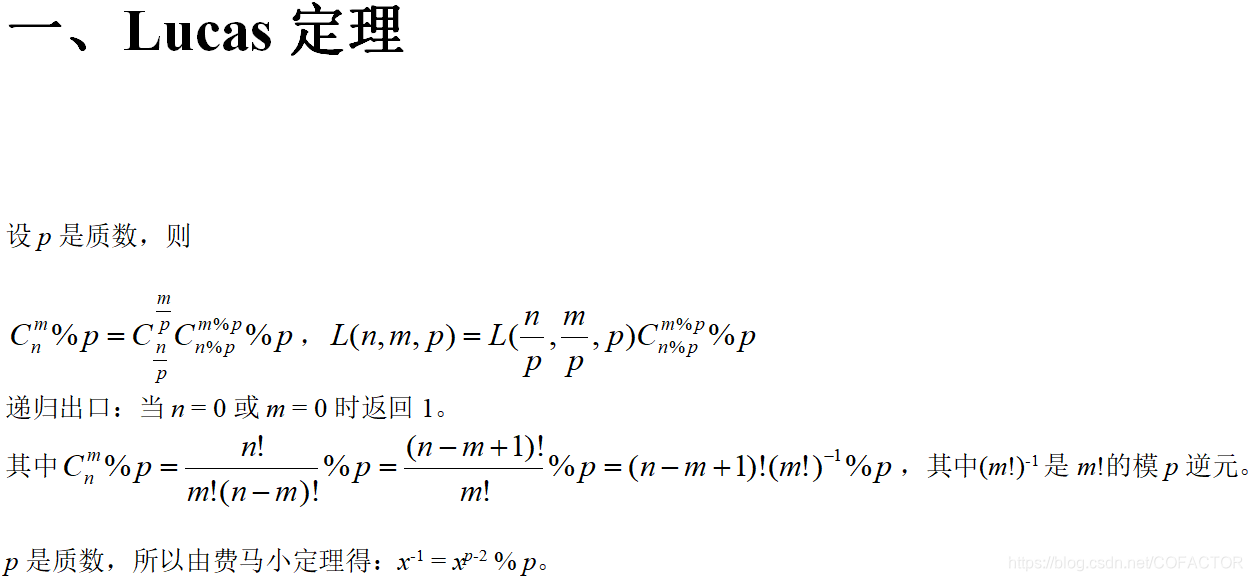
在这里插入图片描述

三、AC 代码

三年 OI 一场空，不开 long long 见祖宗。
——谚语

对本题，如果中间变量不用 long long 或 unsigned long long 表示，5 个点会 WA 掉第一个。

#include<cstdio>
#pragma warning(disable:4996)
template<class _Ty> inline _Ty PowerMod(_Ty radix, _Ty exp, const _Ty& mod) {
	_Ty ans = 1; radix %= mod;
	while (exp) {
		if (exp & 1)ans = (ans * radix) % mod;
		exp >>= 1, radix = (radix * radix) % mod;
	}
	return ans % mod;
}
template<class _Ty> inline _Ty C(const _Ty& n, _Ty m, const _Ty& p) {//Calculate nCm % p, p is prime.
	if (m > n)return 0;
	if (m > n / 2)m = n - m;
	_Ty num = 1, den = 1;
	for (_Ty i = n - m + 1; i <= n; ++i)num = num * i % p;
	for (_Ty i = 1; i <= m; ++i)den = den * i % p;
	return num * PowerMod(den, p - 2, p) % p;
}
template<class _Ty> _Ty lucas(const _Ty& n, const _Ty& m, const _Ty& p) {//Calculate nCm % p, p is prime.
	if (m == 0 || n == 0)return 1;
	return C(n % p, m % p, p) * lucas(n / p, m / p, p) % p;
}
unsigned long long n, m, p, t;
int main() {
	scanf("%llu", &t); ++t;
	while (--t) {
		scanf("%llu%llu%llu", &n, &m, &p);
		printf("%llu\n", lucas(n + m, m, p));
	}
	return 0;
}