【梳理】离散数学 第15章 欧拉图与哈密顿图 15.1 欧拉图 15.2 哈密顿图

教材：《离散数学》第2版 屈婉玲 耿素云 张立昂 高等教育出版社
源文档高清截图在最后

第15章欧拉图与哈密顿图

15.1 欧拉图

1、通过图中所有边仅一次的通路称作欧拉通路。通过图中所有边仅一次的回路称作欧拉回路。具有欧拉回路的图是欧拉图，仅具有欧拉通路的图是半欧拉图。平凡图（只含一个顶点的图）是欧拉图。

2、无向图G是欧拉图，当且仅当G是连通图且没有奇度顶点。
证明 若G为平凡图，显然成立。设该图G(V, E)为非平凡图，具有m条边和n个顶点。
必要性（左推右）。因为G为欧拉图，所以G存在欧拉回路C。对任意vi, vj∈V，vi, vj都在C上。因而vi, vj连通，G为连通图。对任意vi∈V，vi在C上每出现一次就获得两个度（一个入度和一个出度），而所有顶点都会出现在C中至少一次，于是G中无奇度顶点。
充分性（右推左）。由于G为非平凡的连通图，边数m≥1，下面对m作归纳证明。
m = 1时，因为G没有奇度顶点，但G又是连通的，所以G只能是一个环。G为欧拉图。
如果m≤k（k≥1）时结论都成立，那么m = k + 1时结论也要成立。由于G的连通性且无奇度顶点，G的最小度δ(G)≥2。可以证明G中必含圈。设C为G中的一个圈，将删除C中的全部边以后剩下的部分记为G的一个生成子图G’。设G’有s个连通分量G1’、G2’、……、Gs’，其中每个连通分量最多有k条边，且无奇度顶点。设Gi’与C的公共顶点为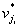，i = 1，2，……，s。由归纳假设，G1’、G2’、……、Gs’都是欧拉图，它们都存在欧拉回路。设Ci是Gi’的一条欧拉回路，i = 1，2，……，s。从某个顶点vr开始沿C行走，遇到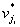就行遍Ci，回到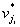继续沿C行走，最后回到vr。于是，走过的这条回路借由G的生成子图G的每个连通分量与G的一条回路C的全部公共顶点，经过了生成子图G’和C的全部边仅一次（因为在连通分量中走的都是欧拉回路），可见走过的这条回路就是G中的欧拉回路，G为欧拉图。
上述充分性证明是构造性证明，提供了一种求欧拉回路的算法：逐步插入回路法。