【DP入门·背包问题·代码超详解】CometOJ C0184 [2006普及组-B]开心的金明

最新推荐文章于 2024-06-01 16:15:35 发布

原创最新推荐文章于 2024-06-01 16:15:35 发布 · 239 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#详解

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

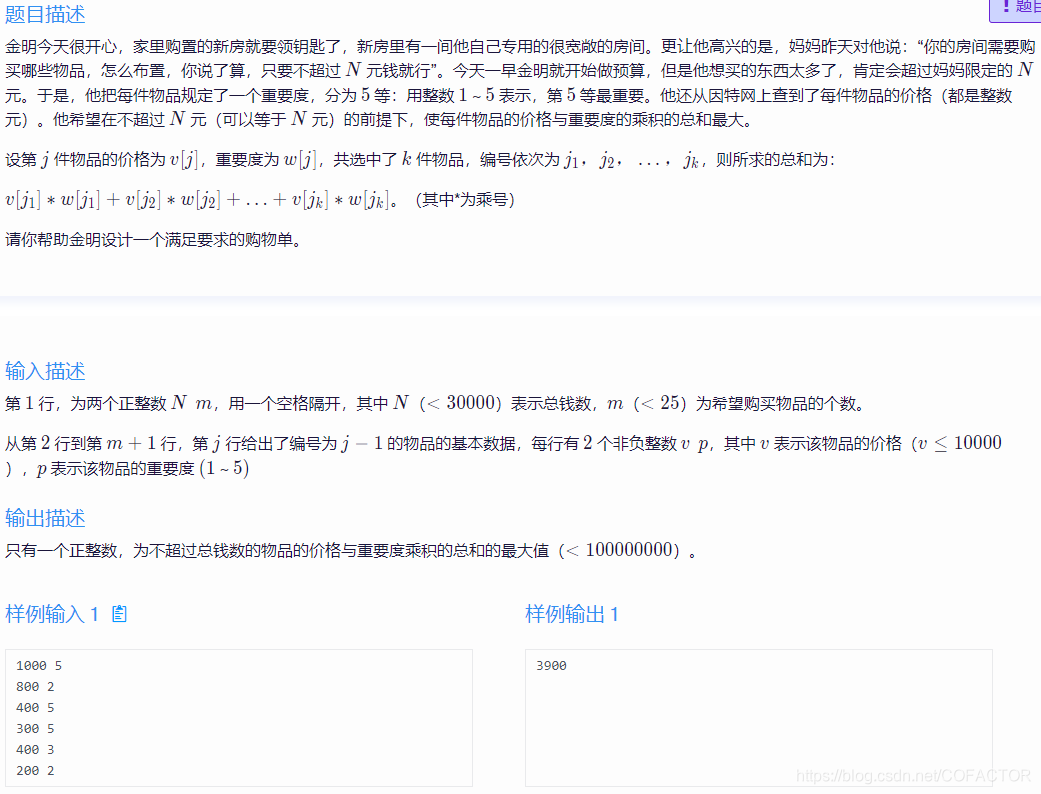
一、题目描述

二、算法分析说明与代码编写指导
最多一共有 24 个物品，每个物品都可以选或者不选，然后考察已选物品总价是否在 N 元的范围内，再计算价格与重要程度的乘积并求和，那么全部 2^24 = 16 777 216 种情况都要计算，有超时的风险。而且，即使这题过了，万一下一题把物品总数改成 100 ，甚至是 1000 ，或更多，怎么办？
我们引入一个新的算法：动态规划（dynamic programming）。
将一个问题拆成几个子问题，分别求解这些子问题，即可推断出大问题的解。
对本例而言，子问题自然就是每个物品选还是不选。
我们可以倒着考虑，将物品从 0 编号至 m - 1 ，先从 m - 1 开始决定每个物品是否选择。设 i 为正在考虑的物品编号，j 为允许的物品总价值，dp[i][j] 为总价格不超过 j 的限制下，第 i 到 m-1 号物品中已选物品的价格与重要程度的积之和的最大值。
如果物品 i 不选（选择 i 则总价格会超过 j），那么已选物品的价格与重要程度的积之和的最大值与已考虑过的 i + 1 到 m - 1 物品的这个最大值一样，所以
dp[i][j] = dp[i + 1][j];
如果可以选择物品 i ，也需要考虑这样的情况：
选了 i ，待求最大值将会累加相应的价格与重要程度的积。但是如果不选 i ，就可以留下更多的钱去选未决定的那些可能具有巨大的价格与重要程度的积的物品。
正如你今晚选择和同学去浪，但是今晚因为去浪而放弃复习的这几道题有可能有不少都出现在了第二天的考卷里。
可见贪心和 DP 的思想一般都是对立的。贪心求解的过程，每一步的决策都是独立的，不会影响前后的决策；而对于那些当前决策可能影响其它决策进而影响最终结果的问题，就不能再贪图眼前的蝇头小利去简单思考。
对本题而言，就是要将选和不选的情形都考虑一下，选择可以获得最大价值的决策。所以
dp[i][j] = std::max(dp[i + 1][j], dp[i + 1][j - v[i]] + v[i] * w[i]);
注意，二维数组的第一个下标只是代表当前正在被决定是否选择的物品编号，不代表这个物品已选或不选。而第二个下标代表允许选择的物品的总价格。如果物品 i 最终选择，那么第二个参数就得改成 j - v[i] ，是因为如果在可用的银子数量为 j 的情况下选了这个价格为 v[i] 的物品，那么剩余的钱就是 j - v[i] 。这 j - v[i] 还未被决定（未被花掉）。这一部分没用掉的钱该怎么用呢？用法只能来自前面已经计算过的结果。所以要考察在总价格限定在 j - v[i] 的时候如何选择前 i + 1 到前 m - 1 个物品。因为是从 m - 1 号物品开始逆向决定是否选择的，所以前 i + 1 到前 m - 1 个物品肯定已经有决定是否选择。当然，这里需要补充一个初始条件：
dp[m][0] = 0;
物品编号是 0 到 m - 1 ，所以 m 物品实际上是不存在的。这个初始条件只是被用于决定 m - 1 号物品是否可以选择。如果 m - 1 不选，那么总的价格与重要程度的积依然是零。如果选，也要根据已有的结果加上 m - 1 物品的价格与重要程度的积。因为选择的是第一个物品，价格与重要程度的积的和仍然是零。所以无论第一个物品选不选，都要用到这个初始条件。
对接下来要选的物品，如果选择，那么也需要引用前面已选物品的价格与重要程度的积的累加结果，然后加上当前选择的物品的价格与重要程度的积。
这就是状态转移方程的来由。
物品 i 可选时，对应的方程也可以这样理解：
当总价格限制为 j 时，可能有如下两种情况：
1、物品 i 不选，因为这 j 元已经在之前选择了总的价格与重要程度之积更高的一些物品。选了 i 的话剩下的 j - v[i] 元只能选一些价格与重要程度之积的总和很低的一些物品。
2、物品 i 要选，因为选了以后总的价格与重要程度之积可以比不选更高。
无论剩下的 N - j 元怎么选，至少前 j 元已经采用了更大的价格与重要程度之积的选择方案。
总价格限制从 0 开始逐渐放开，虽然这很可能也会产生很多与题目无直接关系的中间结果（题目让你用不超过 N 元的总经费去选择哪些物品可以买，但是却把经费从 0 到 N - 1 元的情形都算了一遍），但是相比不利用任何已经计算过的结果的暴力枚举，通过 DP 求解诸如本题这样的背包问题，时间复杂度已经大大降低。因为在决定任何一个物品时，都可以利用初始值（对第一个决定的物品而言）或从这一大堆“草稿”中找到已经决策过的中间结果并加以利用。
最后一个物品（第 0 个）决策完毕后，最终结果保存在 dp[0][n] 中。
此外，也可以先决定 1 号物品，这样初始条件应该改成
dp[0][0] = 0;
而物品编号此时应该是 1 到 n ，最终结果保存在 dp[m][n] 中。算法的原理与倒序递推时是完全一样的。

值得一提的是，这题如果采用 unsigned int 保存全部数据，而将倒序递推写法中的外层循环写成
for(unsigned i = m - 1 ; i != 0xffffffff; --i)
那么执行的速度比 int 类型要慢（具体见下方 AC 代码）。
大多数时候 unsigned 类型都要比对应的 int 类型快一点点（具体见https://blog.youkuaiyun.com/COFACTOR/article/details/99695105）。

但是从本例可见，例外也是有的。猜测可能是
i != 0xffffffff;
条件影响了速度。不过这个就比较玄学，这令我想起一道 POJ 的题（具体见https://blog.youkuaiyun.com/COFACTOR/article/details/100751456）：

其它条件一致，这题如果用 0xFFFF FFFF FFFF FFFF 标记，就会超时。而标记如果写成 0xFFFF FFFF则可以贴着时限通过。

三、AC 代码（2 ms）

#include<cstdio>
#include<algorithm>
#pragma warning(disable:4996)
int v[24], w[24], dp[25][30001], m, n;
int main() {
	scanf("%d%d", &n, &m); dp[m][0] = 0;
	for (int i = 0; i < m; ++i) { scanf("%d%d", &v[i], &w[i]); }
	for (int i = m - 1; i >= 0; --i) {
		for (int j = 0; j <= n; ++j) {
			if (j < v[i])dp[i][j] = dp[i + 1][j];
			else dp[i][j] = std::max(dp[i + 1][j], dp[i + 1][j - v[i]] + v[i] * w[i]);
		}
	}
	printf("%d\n", dp[0][n]);
	return 0;
}

#include<cstdio>
#include<algorithm>
#pragma warning(disable:4996)
int v[25], w[25], dp[25][30001], m, n;
int main() {
	scanf("%d%d", &n, &m); dp[0][0] = 0;
	for (int i = 1; i <= m; ++i) { scanf("%d%d", &v[i], &w[i]); }
	for (int i = 1; i <= m; ++i) {
		for (int j = 0; j <= n; ++j) {
			if (j < v[i])dp[i][j] = dp[i - 1][j];
			else dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - v[i]] + v[i] * w[i]);
		}
	}
	printf("%d\n", dp[m][n]);
	return 0;
}