代码随想录算法训练营day11 | 150.逆波兰表达式求值、239.滑动窗口最大值

150.逆波兰表达式求值

题目链接、文章讲解/视频讲解

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

思路：其实逆波兰表达式相当于是二叉树中的后序遍历。

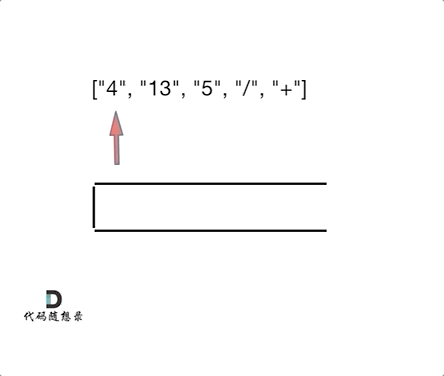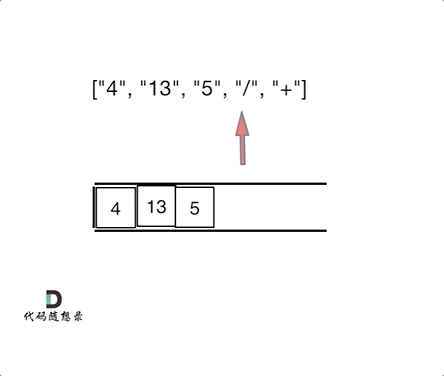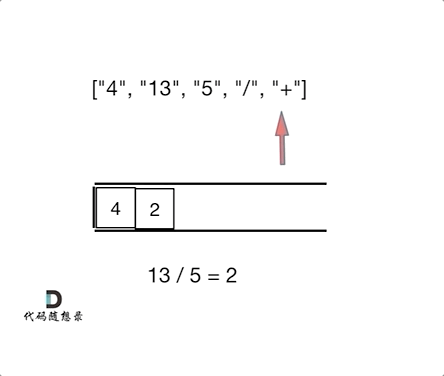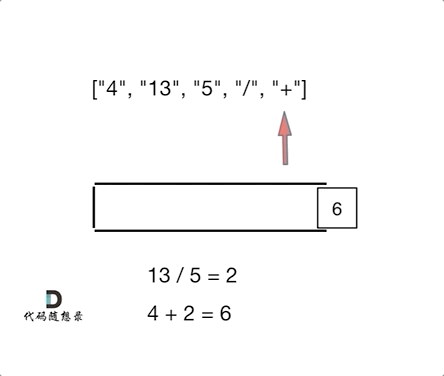
代码如下：

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<long long> st;
        for(int i = 0; i < tokens.size(); i++){
            if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
                long long nums1 = st.top();
                st.pop();
                long long nums2 = st.top();
                st.pop();
                if(tokens[i] == "+") st.push(nums1 + nums2);
                if(tokens[i] == "-") st.push(nums2 - nums1);
                if(tokens[i] == "*") st.push(nums1 * nums2);
                if(tokens[i] == "/") st.push(nums2 / nums1);
            }
            else st.push(stoll(tokens[i]));
        }
        long long result = st.top();
        st.pop();
        return result;
    }
};

239.滑动窗口最大值

题目链接、文章讲解/视频讲解 

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

思路：

队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

那么这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来实现一个单调队列

不要以为实现的单调队列就是 对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。

来看一下单调队列如何维护队列里的元素。

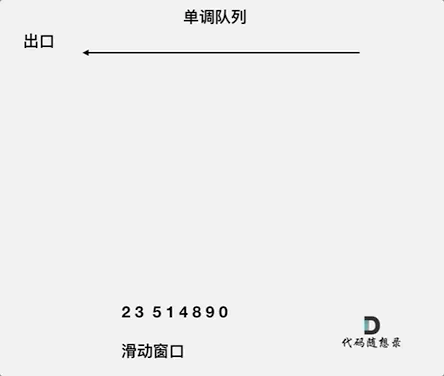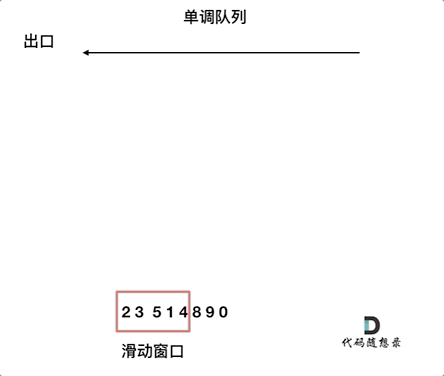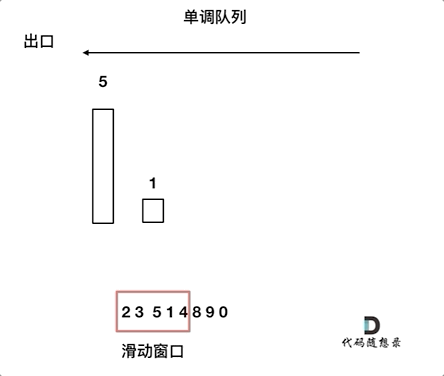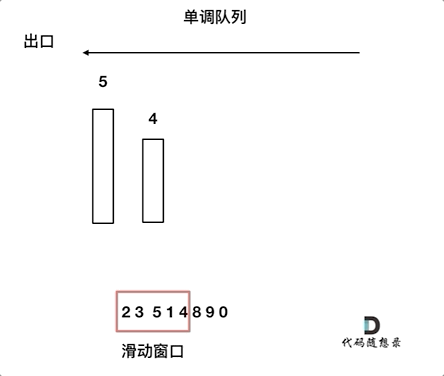
对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。

此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢？

设计单调队列的时候，pop，和push操作要保持如下规则：

1. pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
2. push(value)：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止

保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。

代码如下：

class Solution {
private:
    class Myqueue{
    public:
        deque<int> que;
        void push(int value){
            while(!que.empty() && value > que.back()){
                que.pop_back();
            }
            que.push_back(value);
        }
        void pop(int value){
            if(!que.empty() && value == que.front()) que.pop_front();
        }
        int front(){
            return que.front();
        }
    };

public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        Myqueue que;
        vector<int> result;
        for(int i = 0; i < k; i++){
            que.push(nums[i]);
        }
        result.push_back(que.front());
        for(int i = k; i < nums.size(); i++){
            que.pop(nums[i - k]);
            que.push(nums[i]);
            result.push_back(que.front());
        }
        return result;
    }
};