矩阵快速幂 poj3070

Fibonacci

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 20957		Accepted: 14366

Description

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

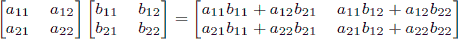Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

 

 

其实矩阵快速幂和数的快速幂很像  其实都用到二分的思想

//矩阵快速幂
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
#define LL __int64
#define MOD 1000
typedef struct MATRIX
{
    int mat[50][50];
}MATRIX;
 
MATRIX mat_multiply (MATRIX a,MATRIX b,int n)
{
    MATRIX c;   //c[i][j]= Σ a[i][k]*b[k][j]
    memset(c.mat,0,sizeof(c.mat));
/*
    for(int i=0;i<n;i++)    //a矩阵一行一行往下
        for(int j=0;j<n;j++)    //b矩阵一列一列往右
            for(int k=0;k<n;k++)    //使a矩阵 第i行第k个元素 乘以 b矩阵 第j列第k个元素
                if(a[i][k] && b[k][j])    //剪枝（添条件，设门槛），提高效率，有一个是0，相乘肯定是0
                    c.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
*/
 
//上面也是可以的，但是下面的剪枝更好一些，效率更高一些，但是运算顺序有点难想通，，，
//上面就是C[i][j]一次就求出来，下面就是每次c[i][j]求出一项【就是上面红体字，每次各求一列】
 
    for(int k=0;k<n;k++)    //这个可以写到前面来，
        for(int i=0;i<n;i++)
            if(a.mat[i][k])     //剪枝：如果a.mat[i][k]是0，就不执行了
                for(int j=0;j<n;j++)
                    if(b.mat[k][j])     //剪枝：如果b.mat[i][k]是0，就不执行了
                    {
                        c.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
                        if(c.mat[i][j]>=MOD)    //这个看实际需求，要不要取模
                            c.mat[i][j]%=MOD;   //取模的复杂度比较高，所以尽量减少去模运算，添加条件，只有当大于等于MOD的时候才取余
                    }
    return c;
}
 
MATRIX mat_quick_index(MATRIX a,int N,int n)
{
    MATRIX E;   //单位矩阵，就像数值快速幂里，把代表乘积的变量初始化为1
 
//    memset(E.mat,0,sizeof(E.mat));  //置零，单位矩阵除了主对角线都是1，其他都是0
//    for(int i=0;i<n;i++)    //初始化单位矩阵【就是主对角线全是1】
//            E.mat[i][i]=1;
 	//把E初始化 单位矩阵(主对角线) 乘与任何矩阵都是它本身 
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            E.mat[i][j]=(i==j); //酷炫*炸天的初始化！！！
 
    while(N>0)
    {
        if(N & 1)
            E=mat_multiply(E,a,n); 
        N>>=1;
        a=mat_multiply(a,a,n);
    }
    return E;
}
 
int main()
{
    int n,N;    //n为矩阵（方阵）规模，几行，N为指数
    MATRIX A,C;
 
    memset(A.mat,0,sizeof(A.mat));
    memset(C.mat,0,sizeof(C.mat));
 
    scanf("%d",&n);     //矩阵规模，这里是方阵，行数等于列数
 
    for(int i=0;i<n;i++)    //初始化A矩阵
        for(int j=0;j<n;j++)
            scanf("%d",&A.mat[i][j]);
 
    scanf("%d",&N);
    C=mat_quick_index(A,N,n);
 
    for(int i=0;i<n;i++)    //打印C矩阵
    {
        for(int j=0;j<n;j++)
            printf("%3d",C.mat[i][j]);
        printf("\n");
    }
    return 0;
}

 

 

此题题解

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
using namespace std;
const int mod=10000;
struct node
{
	int a[2][2];
	node(){
		memset(a,0,sizeof(a));//记得初始化 
	} 
};

node mul(node p,node q)
{
	node t;
	 
	for(int i=0;i<2;i++){
		for(int j=0;j<2;j++){
			for(int k=0;k<2;k++){
				t.a[i][j]=(t.a[i][j]+p.a[i][k]*q.a[k][j])%mod;
			}
		}
	}
	return t;
}

node binary(node e,int n)
{
	node t;
	for(int i=0;i<2;i++){
		for(int j=0;j<2;j++){
			t.a[i][j]=(i==j);
		}
	}
	while(n>0){
		if(n&1){
			t=mul(t,e);
		}
		n>>=1;
		e=mul(e,e);
	}
	return t;
}
int main()
{
	int n;
	while(scanf("%d",&n)==1,n!=-1){
		node e;
		//初始化 
		e.a[0][0]=1;
		e.a[0][1]=1;
		e.a[1][0]=1;
		e.a[1][1]=0;
		node tt=binary(e,n);
		printf("%d\n",tt.a[0][1]);
		
	}
	return 0;
 }