格密码基础（2）-计算性困难问题

基础学习中的一点个人笔记，

​ 这里写的关于格理论的困难问题主要是针对密码学介绍的。上次写到，现代密码学方案大都是基于某个困难问题研究的，最终方案的安全性也被规约到困难问题的安全性上去。

​ 格密码系统的另一个优势就是平均情况下的困难性可以规约到最坏情况下的困难性，在密码系统中我们希望的是任何情况下系统都是安全的，所以平均情况下的安全性是我们想要的。[Ajtai96]给出了最坏情况困难性与平均情况困难性的连接，对于这个重要的结论，我个人的理解是“如果最坏情况下问题是困难的，那么在平均情况下问题就是困难的”（实际上论文中因该是关于SVP问题的具体解释）。

​ SVP，CVP都是基础的计算性困难问题，现在用于构造密码系统的困难问题主要是LWE和SIS问题。SIS以及LWE问题的困难性可以规约到基础的计算性困难问题。就相当于是平均情况到最坏情况的规约。

1.最短向量问题 SVP 及近似

1.1 SVP 问题

---

给定一个基为$B$的格$L(B)$，找到一个最短的非零向量$u$。即$\Vert u\Vert ={\min }_{v\in L}\Vert v\Vert$。

---

上图中，绿色向量为一组基，红色向量即为最短向量。可以看出在2维中，SVP问题并不困难，但是随着维数的提高问题就会变得非常棘手。

1.2 SVP${}_{\gamma }$ 问题

最短向量问题中要求找到是格中最短的非零向量，实际上在一些问题中格中较短向量也是很有用的，所以就有下面一个最短向量的近似版本。

---

给定一个基为$B$的格$L(B)$，找到一个近似最短的非零向量。即$\Vert u\Vert =\gamma {\min }_{v\in L}\Vert v\Vert$。

---

在SVP${}_{\gamma }$问题中我们不要求找到的恰好是最短的向量，我们只要能够得到一个小于$\gamma$倍的最短向量模的向量就可以。

2.最近向量问题 CVP 及近似

2.1 CVP 问题

---

给定一个基为$B$的格$L(B)$，$R^n$空间中的一个向量$t$,找到格中与$t$最近的一个向量$u$。即$dist(t,u)<d$。

---

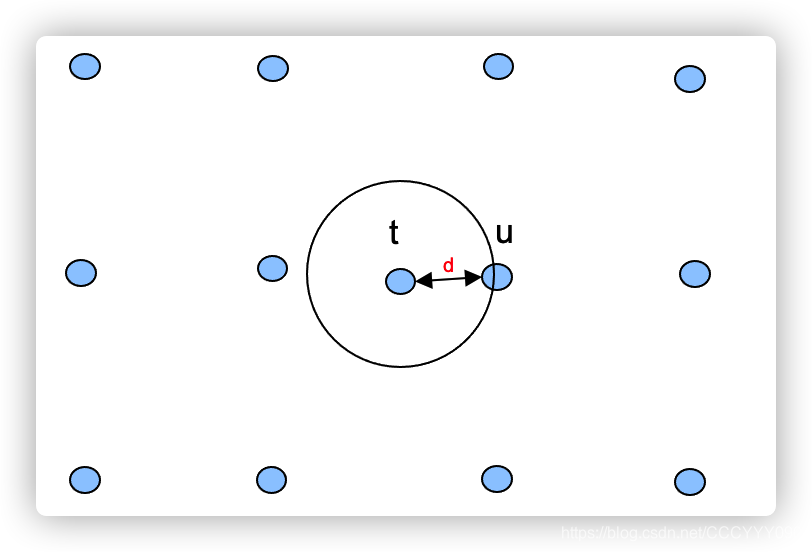
这里我们所说的$d$为格的覆盖半径,在这个半径内的格点我们就认为是他的最近格向量。

2.2 CVP${}_{\gamma }$ 问题

---

给定一个基为$B$的格$L(B)$，$R^n$空间中的一个向量$t$,找到格中的一个向量$u$。即$dist(t,u)<\gamma d$。

---

CVP问题对应的近似问题是在限制距离$d$上放宽了条件，对应解的数量会变多，所以问题会变的相对简单。

3.最短独立向量问题（SIVP）

---

给定基为$B$的格$L(B)$,找到一组线性无关的向量S={s1,…,sn}S=\{s_1,\dots,s_n\}S={s1​,…,sn​}。且$s_i<\gamma {\min }_{v\in L}\Vert v\Vert$

以上为格中基础的计算性困难问题，用于直接构造密码系统的困难问题通常是SIS，LWE。将会在下篇博文中介绍。