%integral
dts =[0.01:0.02:0.5];
eve_err=dts;
evei = 0;
last_sample = 0
for dt = dts
evei =evei+1;
t = [0:dt:2*pi];
dis_int =t;
real_int = t;
dis_tri_int = t;
err1=t;
err3 = t;
err1sum=0;
step = 0;
sum = 0;
sumtri=0;
for i = t
step=step+1;
sum = sum+dt*sin(i);%矩形积分算法
sumtri = sumtri+0.5*dt*(sin(i) +last_sample);%梯形积分算法
last_sample = sin(i) ;
dis_int(step) = sum;
dis_tri_int(step) = sumtri;
real_int(step)= 1-cos(i); % 实际积分结果
err1(step)= abs(real_int(step)-dis_int(step));% 矩形积分误差
err3(step)= abs(real_int(step)-dis_tri_int(step));%梯形积分误差
end
eve_err(evei)= err1sum/length(t);
plot(t, err1,'r.' ,t,err3,'b.')
end
plot(dts,eve_err,'r.')
%plot([t,sit(t.)]
https://blog.youkuaiyun.com/L_smartworld/article/details/81164408
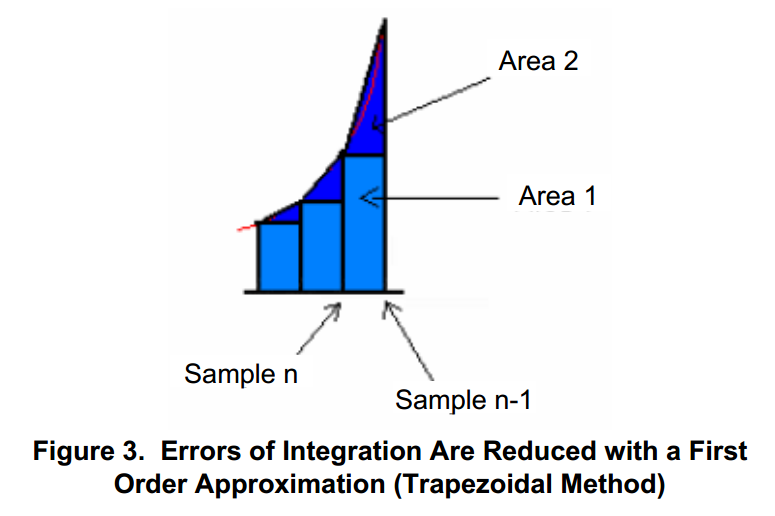








 本文通过Matlab代码详细对比了矩形积分法与梯形积分法的精度差异,使用正弦函数作为积分对象,展示了不同步长下两种方法的积分误差,并以图像形式直观呈现积分效果与误差变化。
本文通过Matlab代码详细对比了矩形积分法与梯形积分法的精度差异,使用正弦函数作为积分对象,展示了不同步长下两种方法的积分误差,并以图像形式直观呈现积分效果与误差变化。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








