Codeforces1129D. Isolation【分块优化DP】

最新推荐文章于 2020-12-05 21:22:14 发布

原创最新推荐文章于 2020-12-05 21:22:14 发布 · 307 阅读

1 ·

CC 4.0 BY-SA版权

DP优化同时被 2 个专栏收录

13 篇文章

订阅专栏

分块

7 篇文章

订阅专栏

本文深入探讨一种解决特定类型动态规划问题的高效算法——区间分块DP。通过实例讲解了如何利用线段树和散点修改技巧优化复杂度，实现快速求解区间内元素出现次数限制的方案数量。适用于大数据量的序列处理，如长度为10^5的数组操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：

给出长度为 $n(1≤n≤10^5)$ 的数组 $a(a_i≤n)$ 。给出 $1 \leq k \leq n$ ，求把这个序列分成若干块的方案，使得对于每个区间，只出现一次的数字不超过k kk个。

题目分析：

$O(n^2)$ 的DP很显然 $f[i]=∑f[j−1]，j满足[j,i]中只出现一次的数≤kf[i]=\sum f[j-1]，j满足[j,i]中只出现一次的数\le k$
考虑如何快速得到 $f [j - 1]$ 的和，从后往前看，把数第一次出现的位置+1，第二次出现的位置-1，那么后缀和就表示 $[j, i]$ 中只出现一次的数的个数。
假设已经求出了 $f [i]$ ，考虑新加入的 $a_{i+1}$ 对后缀和的影响。
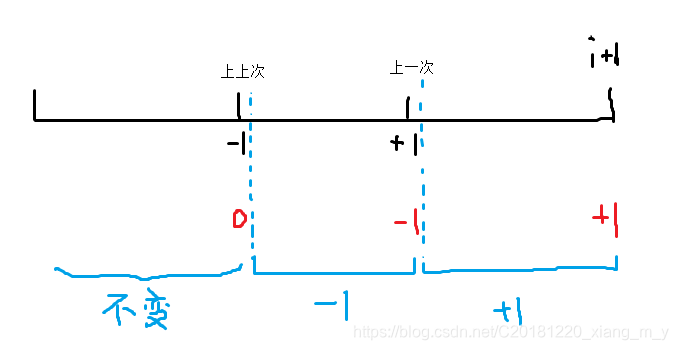
在这里插入图片描述
就是一个区间修改+1或-1，修改之后统计满足条件的f的和。
线段树不好处理<=k的问题，考虑分块。
需要记录 $s [块] [后缀和]$ 表示第几个块后缀和为几的f值的和， $c n t [n]$ 表示每个位置的后缀和， $t a g [块]$ 表示整块修改的标记。
整块修改需要改ans（把s中后缀和在k边界的部分加上或减去）和tag。
散点修改需要改ans和s，先去掉贡献，修改cnt之后再加上贡献。
注意访问后缀和为k的f和，实际上需要访问 $s [] [k - t a g + O]$ ，由于cnt可能为负，所以加上O(=n)的偏移量。

Code：

#include <bits/stdc++.h>
#define maxn 100005
#define S 330
using namespace std;
const int mod = 998244353;
int n,k,a[maxn],pre[maxn],last[maxn];
int s[maxn/S+5][maxn<<1],O,tag[maxn/S+5],cnt[maxn],f[maxn],bel[maxn],ans;
inline void add(int &x,int y){x+=y+(x+y>=mod?-mod:0);}
void ins(int u,int v){
	add(ans,v),add(s[bel[u]][cnt[u]+O],v);
}
void mdf(int u,int v){//单点修改
	if(cnt[u]+tag[bel[u]]<=k) add(ans,mod-f[u-1]);
	add(s[bel[u]][cnt[u]+O],mod-f[u-1]);
	cnt[u]+=v;
	if(cnt[u]+tag[bel[u]]<=k) add(ans,f[u-1]);
	add(s[bel[u]][cnt[u]+O],f[u-1]);
}
void Modify(int L,int R,int v){
	if(L>R) return;
	if(bel[L]+1>=bel[R])
		for(int i=L;i<=R;i++) mdf(i,v);
	else{
		for(int i=L;i<=bel[L]*S;i++) mdf(i,v);
		for(int i=(bel[R]-1)*S+1;i<=R;i++) mdf(i,v);
		for(int i=bel[L]+1;i<bel[R];i++){//整块修改
			if(v==1) add(ans,mod-s[i][k-tag[i]+O]);
			else add(ans,s[i][k+1-tag[i]+O]);
			tag[i]+=v;	
		}
	}
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]),pre[i]=last[a[i]],last[a[i]]=i;
	for(int i=1;i<=n;i++) bel[i]=(i-1)/S+1;
	f[0]=1,ins(1,1);
	for(int i=1;i<=n;i++){
		Modify(pre[i]+1,i,1);
		Modify(pre[pre[i]]+1,pre[i],-1);
		ins(i+1,f[i]=ans);//需要把f[i]加入贡献中
	}
	printf("%d\n",f[n]);
}