拓扑问题1（普通版）

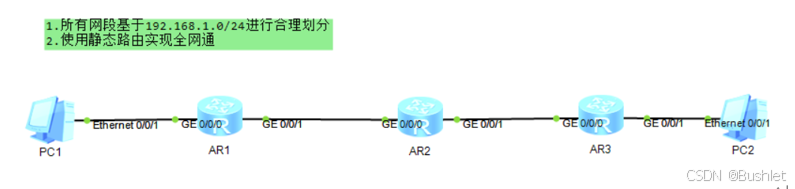
如图中给出的题目来看，要是想实现全网通且他们还不能在同一网段里是时，就需要考虑应该需要多少个网段才可以。  

因为我们知道每个路由器的接口都是一个网段的“大门”，所以上图当中需要4个网段就能够实现全网通。

此时我们就可以对目标网段进行子网划分-----VLSM 

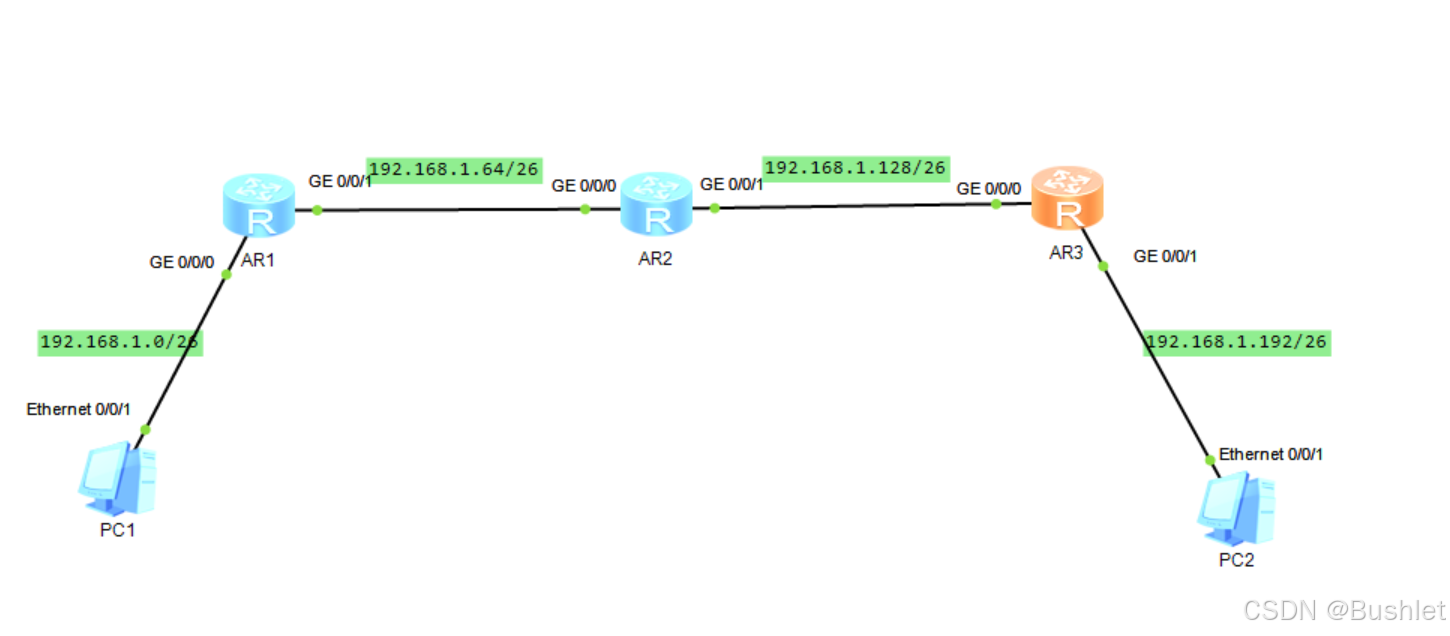
由图中192.168.1.0/24这个网段中进行划分，分成4段网段故我们需要借2位主机位，过程如下图：

将其都分给图中网段可得：

接下来开始实现全网通（配置静态路由）：

1.接口的IP地址

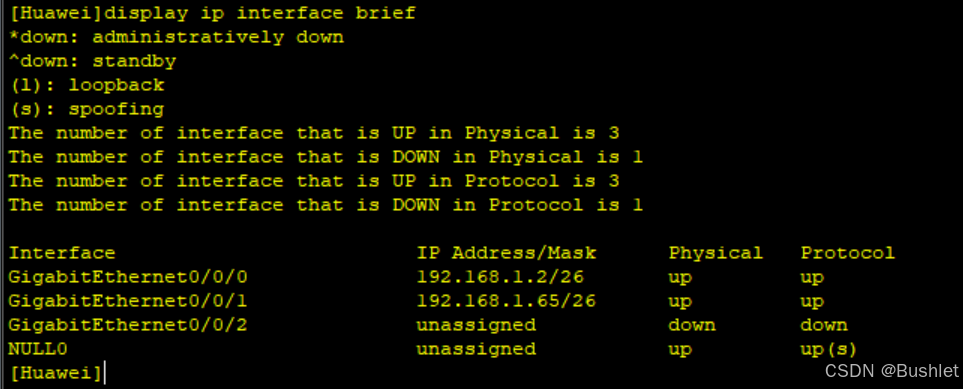
AR1：

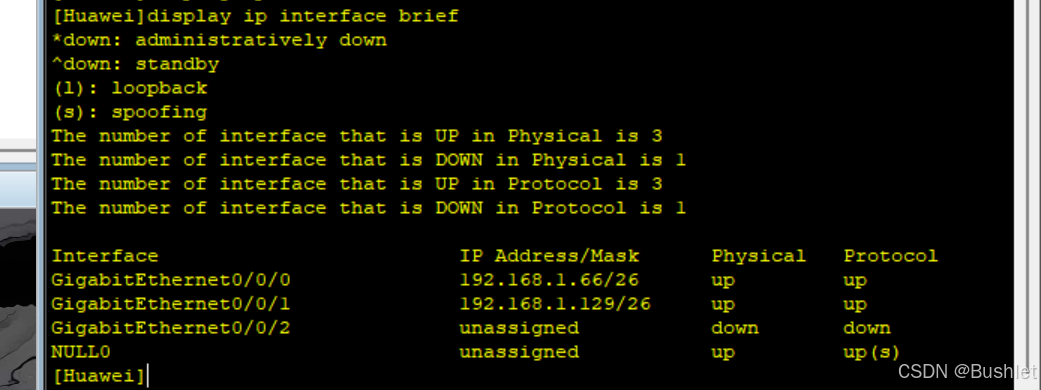
 AR2：

AR3： 

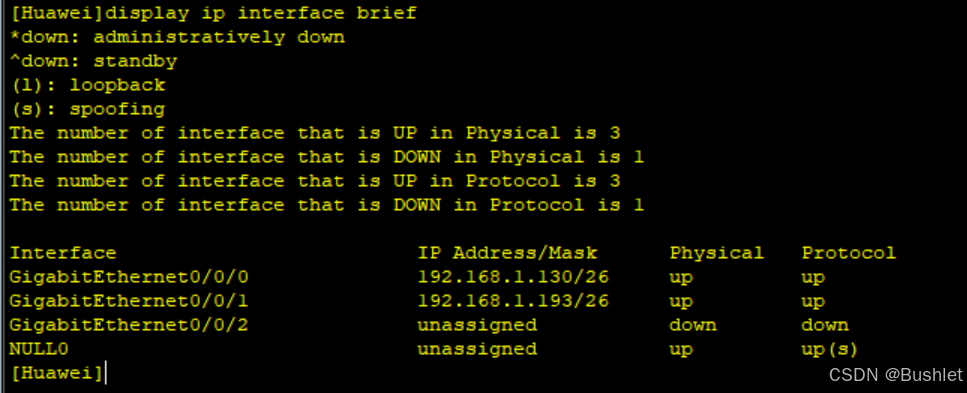
2.跨越网段

AR1: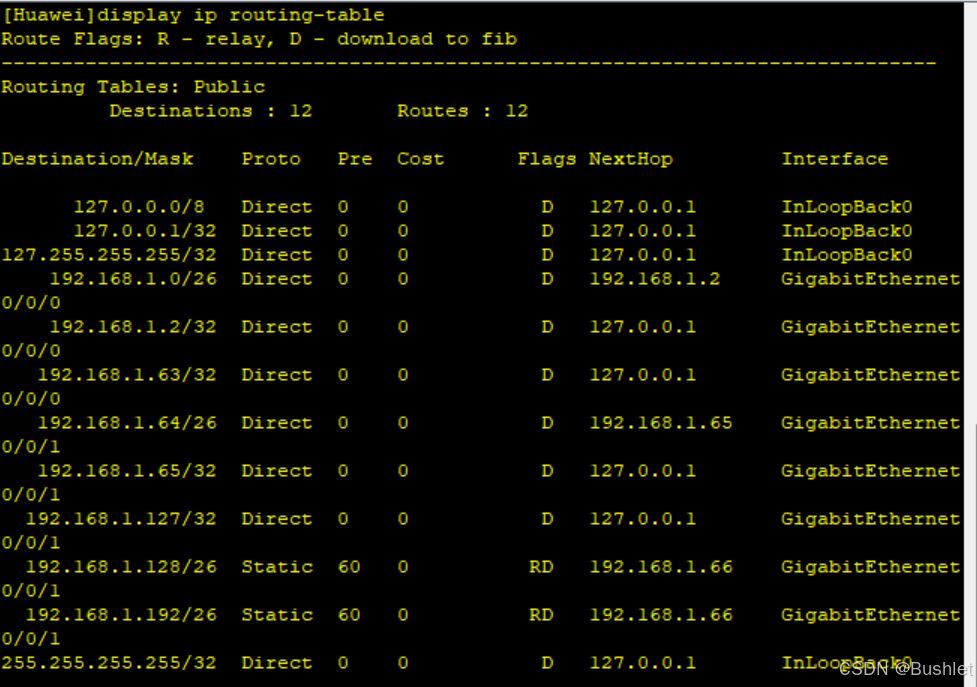

AR2:

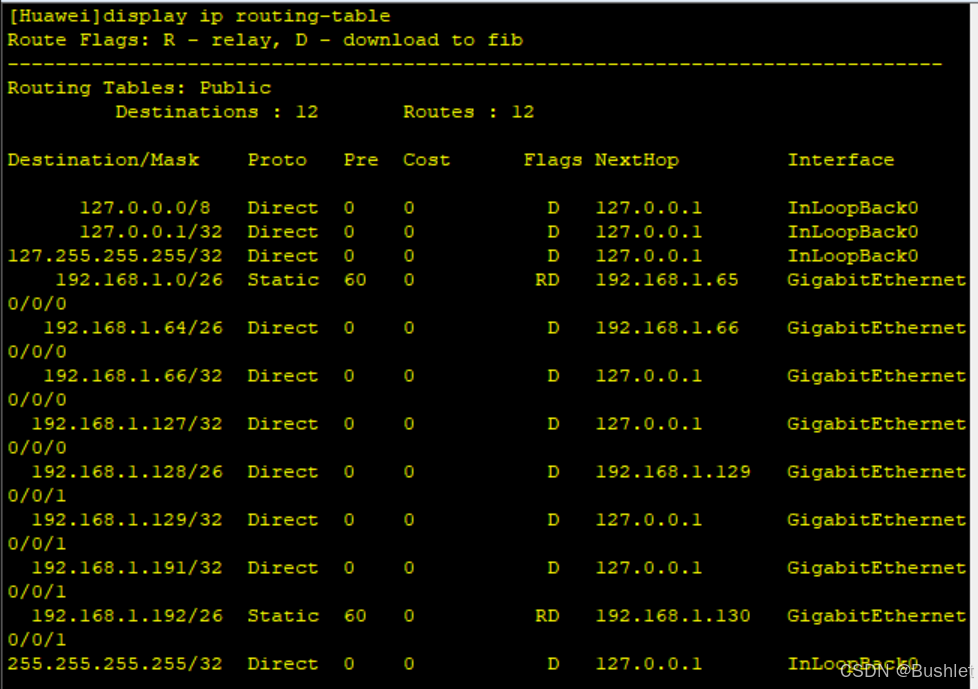
AR3:

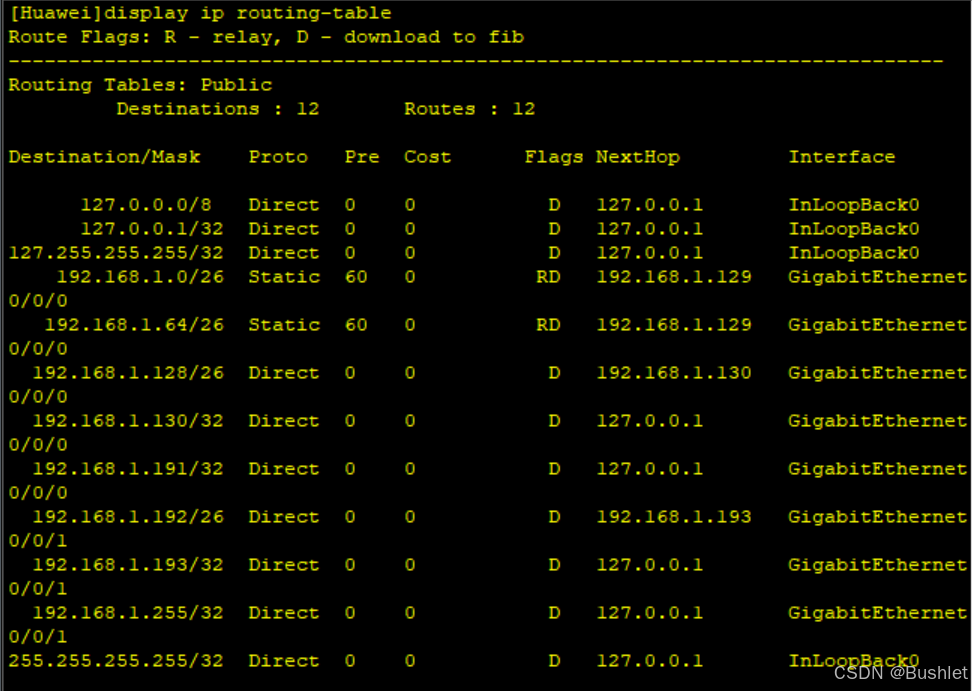
3.对PC端的IP地址进行手动输入

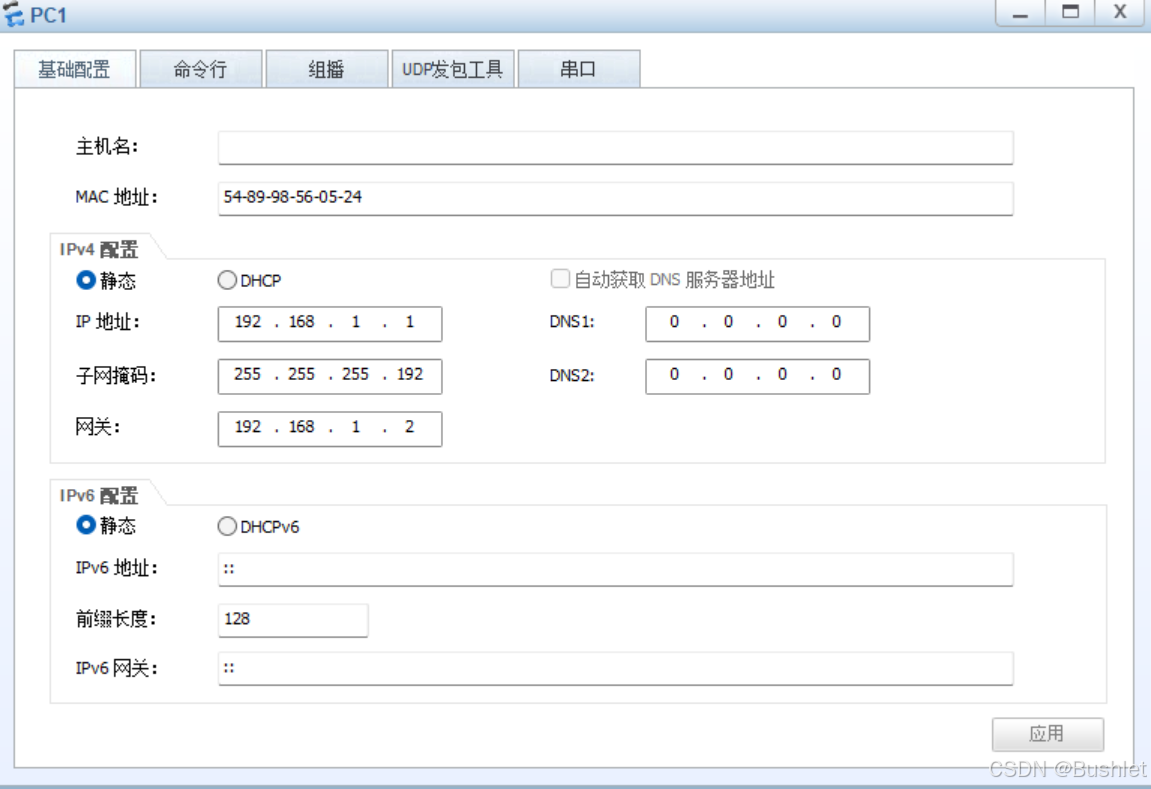
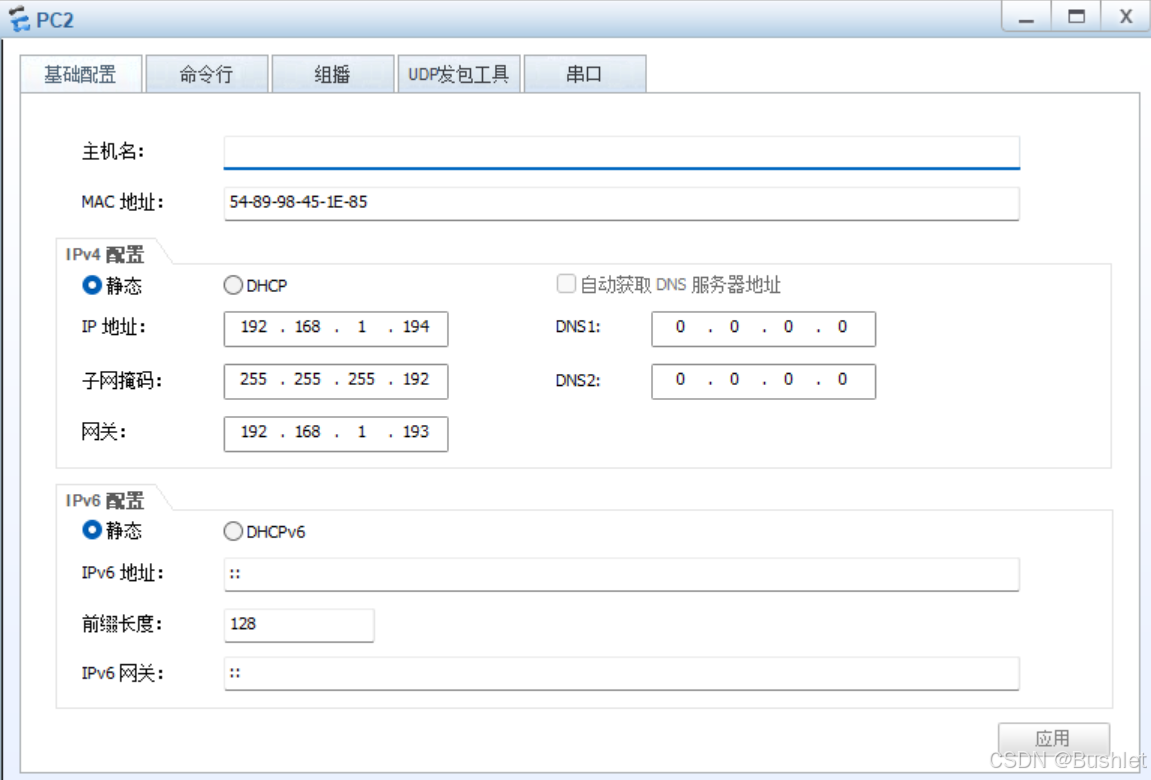
结果：

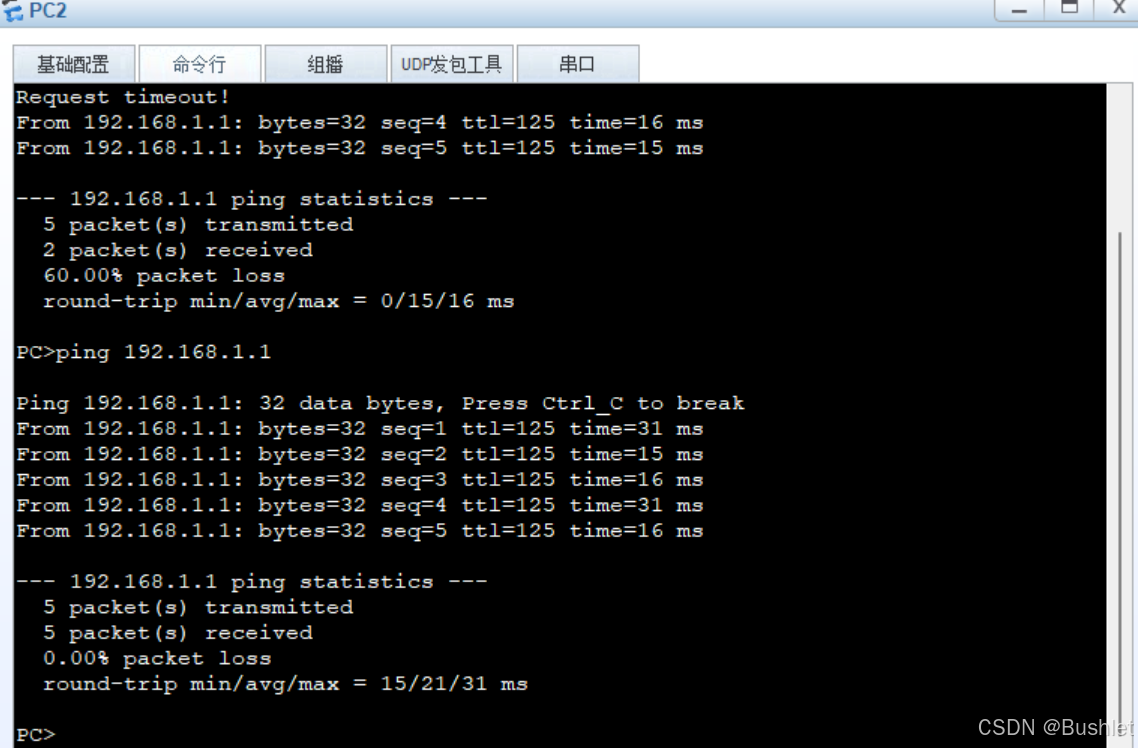
总结：当面对多网段拓扑进行全网通时：

1.先提前考虑好网段的划分

2.根据划分好的网段进行接口的IP地址配置

3. 进行网段的跨越（下一跳）

4.配置PC端的IP地址配置 

提示：写的时候要细心，避免出现错误