最小样本量n的选择

最新推荐文章于 2025-09-14 12:15:00 发布

原创最新推荐文章于 2025-09-14 12:15:00 发布 · 2.8k 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#概率论 #数据挖掘 #数据分析 #python

数据分析专栏收录该内容

27 篇文章

订阅专栏

本文探讨了在假设检验中选择最小样本量的重要性，特别是在数据挖掘和数据分析中。通过介绍点击率检验，阐述了确定研究对象、选择检验方法和计算最小样本量的过程。文章以Python的statsmodels包为例，展示了如何计算最小样本量，并指出样本量、显著性水平α、检验功效（1-β）、效应量之间的关系。最后，提出了一个开放性问题关于期望效果变化对样本量的影响。

1 前言

读曼昆的经济学原理的时候，印象最深刻的一句话是：People face trade-offs, the cost of something is what you give up to get it. 简单来说就是事物都有成本，每个选择都面临取舍。这句话在生产环境中尤为合适。当研发新药的时候，当金融机构对策略进行分析的时候，当判断系统某个新功能是否有效的时候，在一切需要假设检验的地方，就会面临检验样本量的选择。样本量太小，则检验的可信度不高，没有说服力；样本量太大，则成本过高，不可取。在这种情况下，如何选择使样本有代表性、使检验有效的最小样本量变得尤其重要。

2 过程介绍

开始之前先回顾一下假设检验的基础概念。类似于反证法，通常我们将想要拒绝的假设（比如实验组与对照组无差异）设为原假设（H0)，想要证明的假设（双边：实验组与对照组显著不同；单边：实验组明显优于/劣于对照组）设为备择假设（H1）。实验目的为推翻原假设。

犯第一类错误（拒真）的概率为α，也叫做显著性水平；第二类错误（受伪）的概率为β。则检验功效（power of effect）为1-β，也就是当原假设为假时，正确拒绝原假设的概率。

此外，检验效应量（effect size）是衡量效应大小的指标，可以用来反映具有显著差异的研究结果是否具有实际意义或重要性。它通常是均值的组间差值或标准化差值，比率的组间差值或比值(RR、HR)、OR，或相关系数、回归系数等。由于效应量是事后的概念，而最小样本量选取是事前的概念，因此通常可通过历史数据或预期本次试验结果得出所需要的效应量。

2.1 确定研究对象

在考虑用什么检验方法之前，首先要明确的是我们的研究对象。考虑的思路如下：

比较的是均值还是方差？（影响检验方法的选择）；
如果是均值，是绝对值（点击量）还是比率（点击率）？（影响标准差的计算）
是有放回抽样还是无放回抽样？（影响标准差的计算）
独立样本还是不独立？（影响标准差的计算）
方差已知还是未知？（影响分布的选择）
单样本还是两样本？（影响标准差的计算）
单边检验还是双边检验？（影响查表统计量分位数α或α/2的选择）
等等。

考虑到方差的检验可以另开一篇方差分析来讲（包括F检验，ANOVA等），这里我们侧重均值/比率的假设检验。

2.2 确定检验方法

明确好研究对象之后，我们就可以选择合适的检验方法。若对象为均值，多采用Z检验/t检验；若为比率，则可以考虑采用卡方检验。当确定了检验方法，我们可以写出统计量的公式，反推之后即可得到最小样本量n的计算公式。统计量公式繁多，这里不再赘述。均值公式举例如下图。注意，如为双边检验，则将α改成α/2即可。

均值的检验方式选择

2.3 点击率检验举例

在生产环境中AB test经常被提到，比如当前用户在app上看到的是A型广告，我们想知道如果换成B型广告，点击率是否会优于A。考虑到点击或不点击服从（0，1）离散Bernoulli分布，这个问题其实是一个比率的两样本卡方检验，也是一个二乘二列联表检验，这里也等同于z检验。假设当前A型广告点击率为30%，我们希望B型广告能提升10%的点击率至30%*1.1=33%。当两组样本的样本量和方差相似时，可用Cohen’s d 来计算标准均差从而衡量效应量。带入最小样本量n的计算公式中可得每组的n为1881，因此总样本量为3762。计算由下一节中代码实现。

2.4 代码实现

最小样本量计算的代码实现有很多种方式，常用的如Python中的statsmodels包。

from statsmodels.stats.power import GofChisquarePower
from statsmodels.stats.power import zt_ind_solve_power
from statsmodels.stats.proportion import proportion_effectsize as es
#卡方检验
#设定显著性水平为0.05，检验功效为0.8，效应量为标准均差计算方式，对照组和实验组的（预期）比率分别为30%和33%，实验组和对照组数量相等，双边检验。
GofChisquarePower().solve_power(effect_size=es(prop1=0.33, prop2=0.30, method= 'normal'), alpha=0.05, power=0.8,n_bins=2)
#z检验
#设定显著性水平为0.05，检验功效为0.8，效应量为标准均差计算方式，对照组和实验组的（预期）比率分别为30%和33%，实验组和对照组数量相等，双边检验。
zt_ind_solve_power(effect_size=es(prop1=0.33, prop2=0.30, method= 'normal'), alpha=0.05, power=0.8, ratio=1.0, alternative="two-sided")

结果如下。

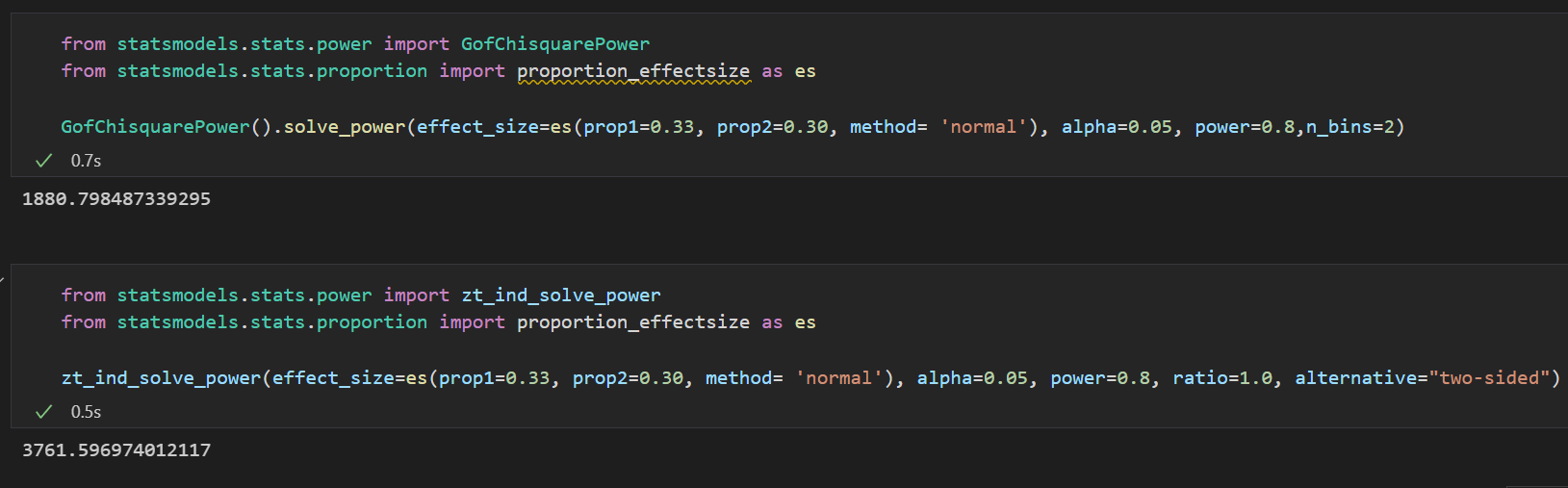
最小样本量计算结果

注意此处为过剩近似，且卡方检验显示的最小样本量为每组样本量，z检验显示的最小样本量为试验的总样本量。可知每组最小样本量为1881，总样本量为3762。

此外：常用α为0.05，常用β为0.2。从中我们也可以看出偏好。人们倾向于严格控制拒真的概率，为此宁愿付出接受错误原假设的代价。

3 小结

假设检验方法千千万，但万变不离其宗。只要明确了研究对象，接下来的步骤就顺理成章非常顺滑。样本大小、显著性水平α、检验功效（1-β）、效应量，给定其中任意三个量，我们就可以推算出第四个量。网络上也有很多现成的AB test计算器，例如Evan's Awesome A/B Tools[1]，可供大家参考。

最后留一个开放性问题。还是刚刚的例子，当期待B型广告的点击率提升得更多时，需要的最小样本量是增多还是减少呢？