0-1背包问题利用Python实现
1,问题描述
背包问题指这样一类问题,题意往往可以抽象成:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。(来自百度百科)
这次课老师给了我们50组数据,依次按物品编号、物品重量和物品价值顺序如图: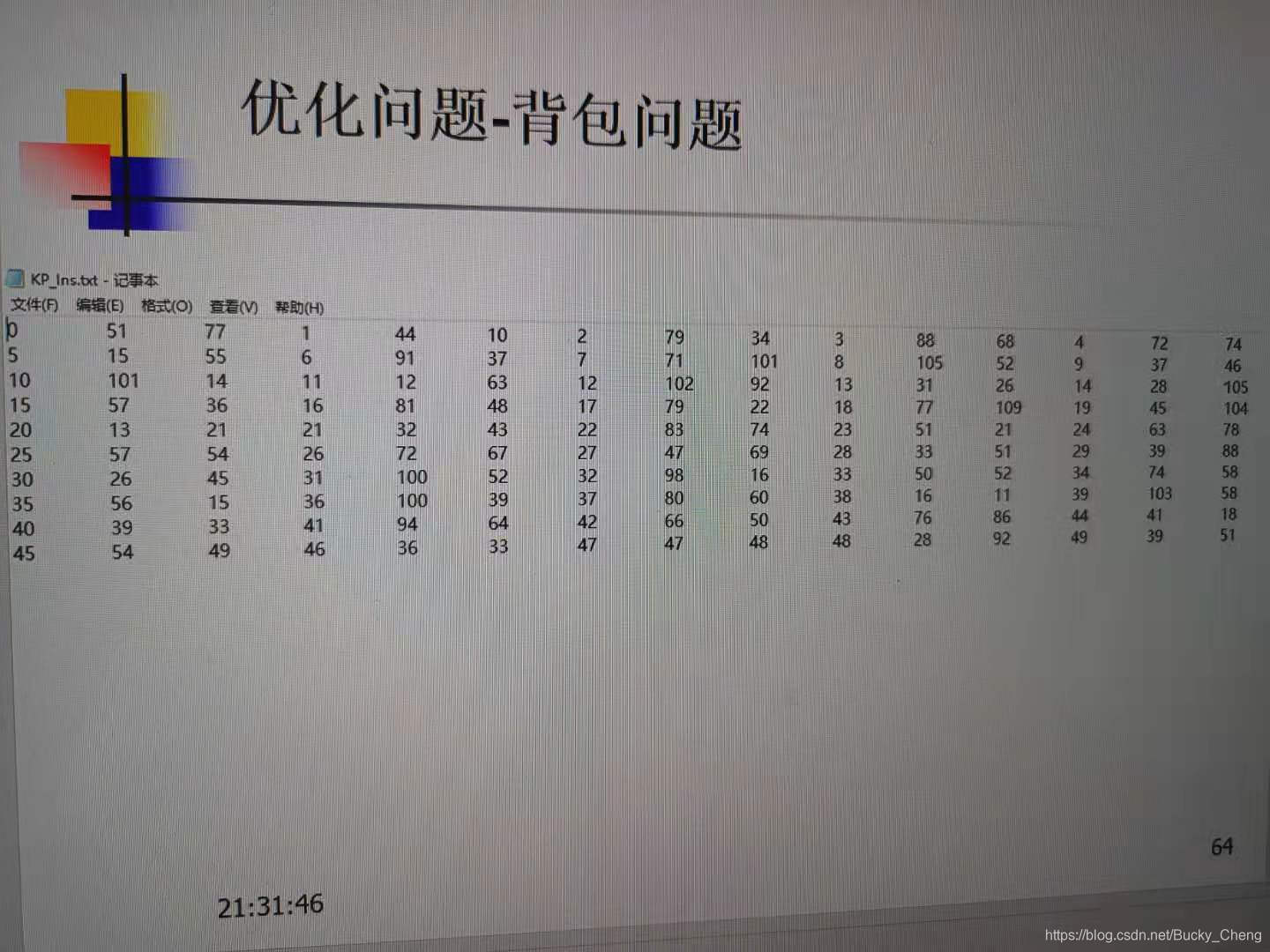
2,算法实现
def dp(weight, count, weights, costs):
"""
动态规划模板,时间复杂度O(weight * count), 空间复杂度O(weight)
:param weight: 背包最大能装的重量
:param count: 物品数量
:param weights: 每件物品的重量
:param costs: 每件物品的价值
:return: 背包装下的最大价值
"""
pre, cur = [0] * (weight + 1), [0] * (weight + 1)
for i in range(count):
for j in range(weight + 1):
if weights[i] <= j:
cur[j] = max(pre[j], costs[i] + pre[j - weights[i]])
pre = cur[:]
return cur[weight]
# count:物品数量; weight:背包总重量; costs: 每件物品的价值; weight:每件物品的重量
count, weight = 50, 1500
costs = [77,10,34,68,74,55,37,101,52,46,14,63,92,26,105,36,48,22,109,104,21,43,74,21,78,
54,67,69,51,88,45,52,16,52,58,15,39,60,11,58,33,64,50,86,18,49,33,48,92,51]
weights = [51,44,79,88,72,15,91,71,105,37,101,12,102,31,28,57,81,79,77,45,13,32,83,51,63,
57,72,47,33,39,26,100,98,50,74,56,100,80,16,103,39,94,66,76,41,54,36,47,28,39]
print(dp(weight, count, weights, costs))
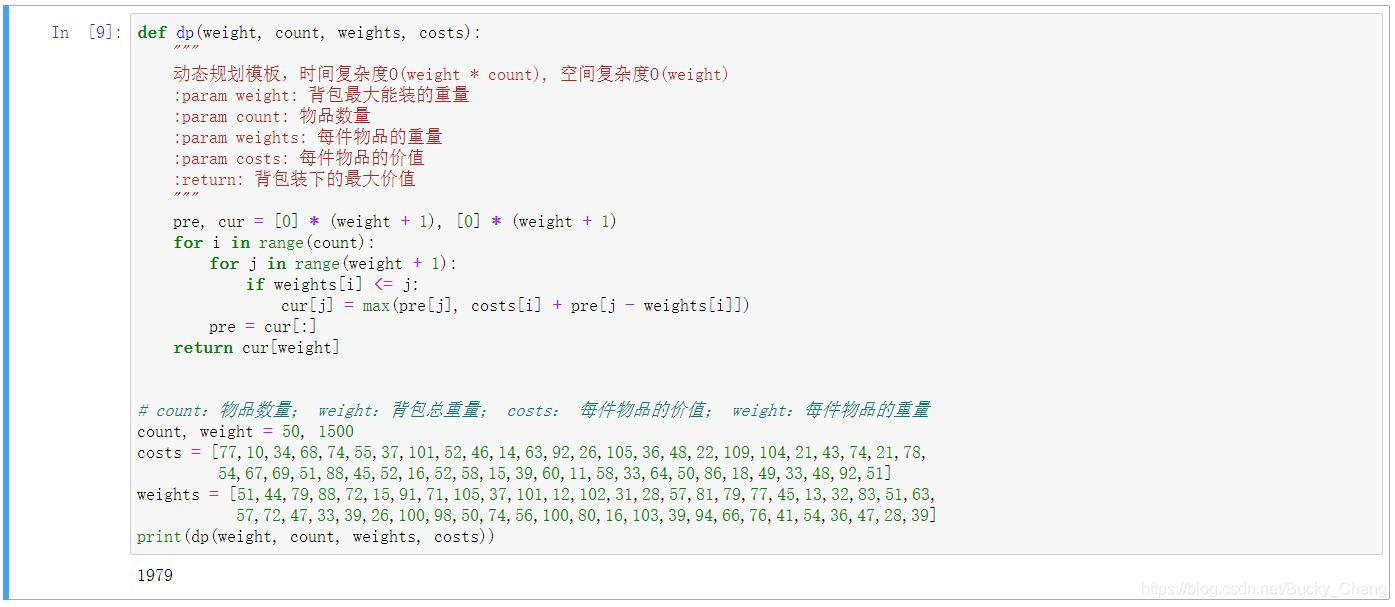
利用Jupyter Notebook(python3)实现得出最优解为1979。
3,后续改进
上述算法只得出了最终的最优解,但是未得到实现最优解的物品编号,需要有后续改进得出最完整的算法程序。
def dp(weight, count, weights, costs):
"""
动态规划模板,时间复杂度O(weight * count), 空间复杂度O(weight)
:param weight: 背包最大能装的重量
:param count: 物品数量
:param weights: 每件物品的重量
:param costs: 每件物品的价值
:return: 背包装下的最大价值
"""
pre, cur = [0] * (weight + 1), [0] * (weight + 1)
for i in range(count):
for j in range(weight + 1):
if weights[i] <= j:
cur[j] = max(pre[j], costs[i] + pre[j - weights[i]])
pre = cur[:]
return cur[weight]
def show(count,weight,weights,value):
print('最大价值为:', value[count][weight])
x = [False for i in range(count)]
j = weight
for i in range(count, 0, -1):
if value[i][j] > value[i - 1][j]:
x[i - 1] = True
j -= weights[i - 1]
print('背包中所装物品为:')
for i in range(count):
if x[i]:
print('第', i+1, '个,', end='')
# count:物品数量; weight:背包总重量; costs: 每件物品的价值; weight:每件物品的重量
count, weight = 50, 1500
costs = [77,10,34,68,74,55,37,101,52,46,14,63,92,26,105,36,48,22,109,104,21,43,74,21,78,
54,67,69,51,88,45,52,16,52,58,15,39,60,11,58,33,64,50,86,18,49,33,48,92,51]
weights = [51,44,79,88,72,15,91,71,105,37,101,12,102,31,28,57,81,79,77,45,13,32,83,51,63,
57,72,47,33,39,26,100,98,50,74,56,100,80,16,103,39,94,66,76,41,54,36,47,28,39]
show(count,weight,weights,value)
print(dp(weight, count, weights, costs))
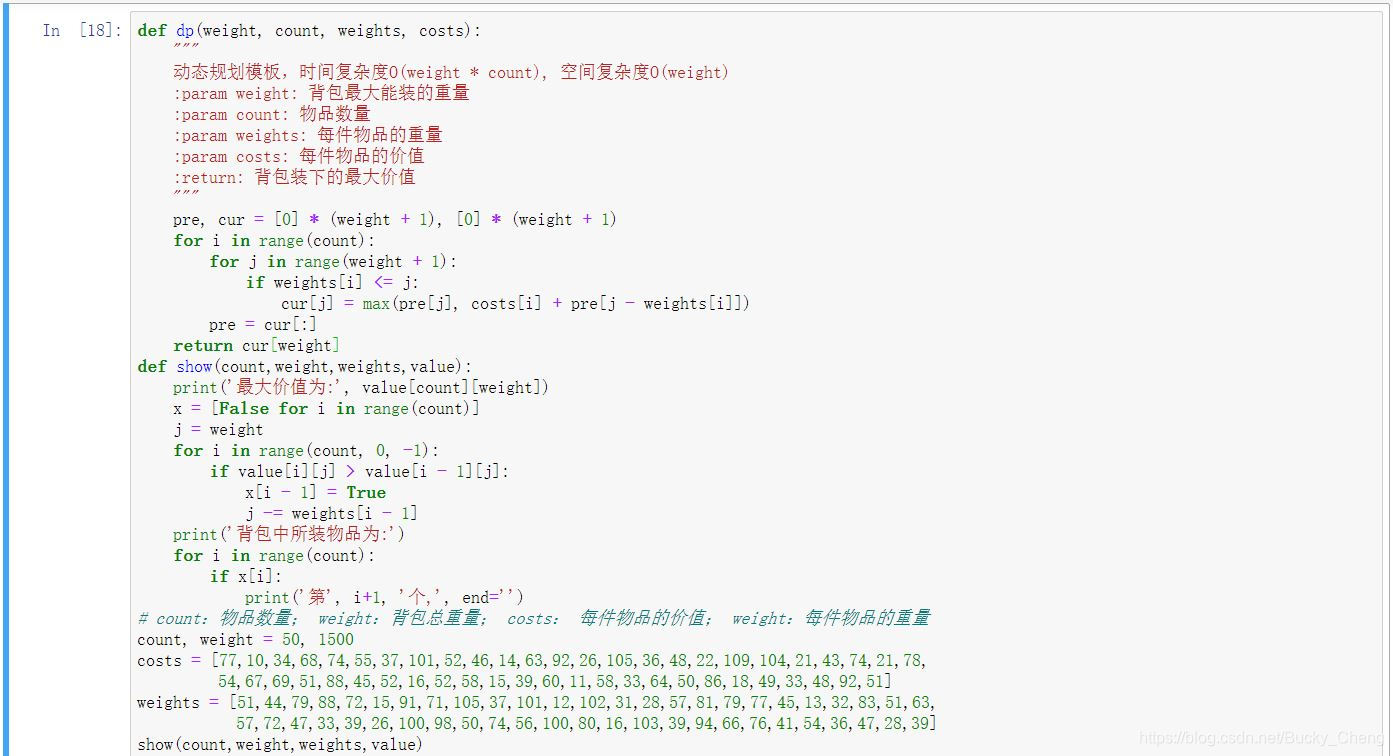








 本文介绍了一种使用Python动态规划解决0-1背包问题的方法,通过具体实例展示了算法实现过程,并给出了求解最优解及对应物品的完整代码。
本文介绍了一种使用Python动态规划解决0-1背包问题的方法,通过具体实例展示了算法实现过程,并给出了求解最优解及对应物品的完整代码。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








