[Java 算法] 二叉树(1)

1.前序遍历+中序遍历确定二叉树

图解:

2.二叉树的( 层序 )遍历相当于广度优先遍历，( 前序 )遍历相当于深度优先遍历

3.在完全二叉树中，若节点编号为 i（i≥1），则其父亲节点的编号为 ⌊i/2⌋（向下取整）

4.完全二叉树

5.二叉树表示方法

二叉树常用的表示方式有二叉链（每个节点有两个指针，分别指向左、右子节点）和三叉链（每个节点有三个指针，除了左、右子节点指针，还有指向父节点的指针）

6.结点的度数

7给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点

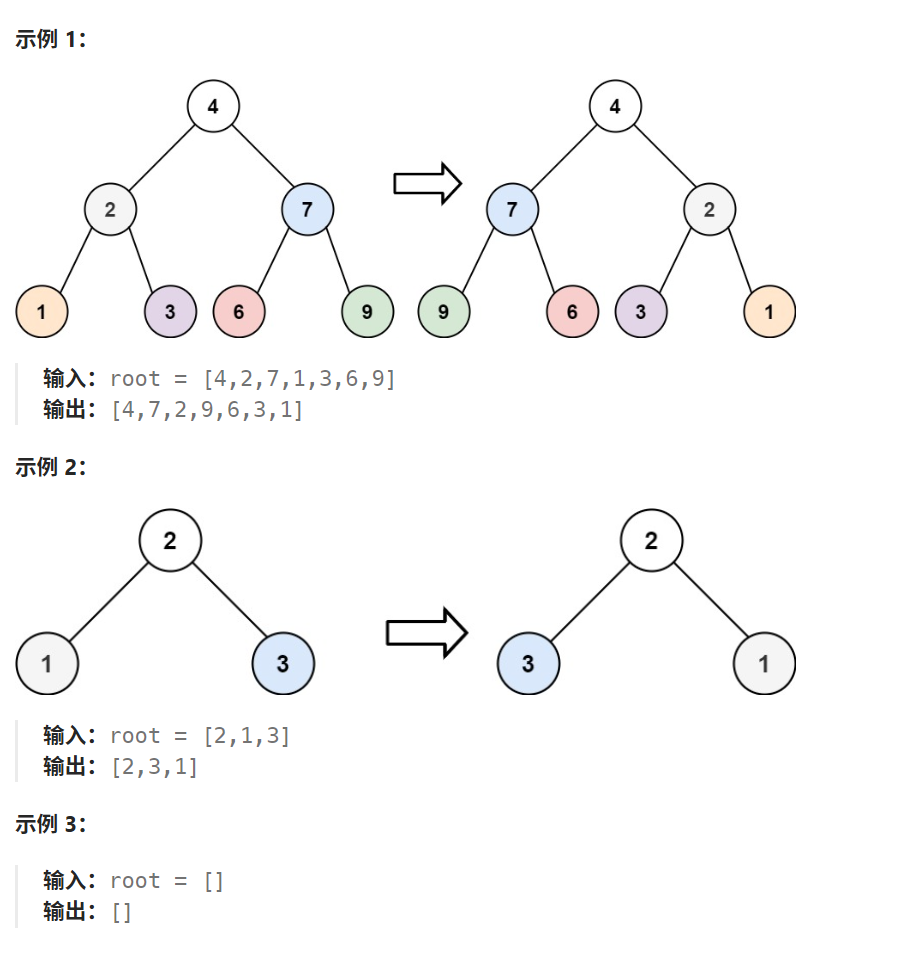
public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        if(root.left == null&&root.right == null){
            return root;
        }
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }

8判断两棵树是否相同

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

public boolean isSameTree(TreeNode p, TreeNode q) {
    //判断两个树的结构是否一样
    if(p != null && q == null || p == null && q != null) {
        return false;
    }
    //如果第一个if 语句没有执行
    //要么都为空 要么都不为空
    if(p == null&&q == null){
        return true;
    }
    //不为空比较两个结点的值
    if(p.val!=q.val){
        return false;
    }

    return isSameTree(p.left,q.left)&&
    isSameTree(p.right,q.right);

}

9给你一个二叉树的根节点 root ， 检查它是否轴对称

public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return isSymmetricN(root.left,root.right);
    }
    public boolean isSymmetricN(TreeNode leftTree,TreeNode rightTree){
        if(leftTree==null&&rightTree!=null||leftTree!=null&&rightTree==null){
            return false;
        }if(leftTree==null&&rightTree==null){
            return true;
        }
        if(leftTree.val!=rightTree.val){
            return false;
        }
        return isSymmetricN(leftTree.left,rightTree.right)&&isSymmetricN(leftTree.right,rightTree.left);
    }

10给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树

public boolean isSubtree(TreeNode root, TreeNode subRoot) {
    if(root == null){
        return false;
    }
    if(isSameTree(root,subRoot)){
        return true;
    }

    return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot);
}
//判断两棵树是否相同
public boolean isSameTree(TreeNode p, TreeNode q) {
    //判断两个树的结构是否一样
    if(p != null && q == null || p == null && q != null) {
        return false;
    }
    //如果第一个if 语句没有执行
    //要么都为空 要么都不为空
    if(p == null&&q == null){
        return true;
    }
    //不为空比较两个结点的值
    if(p.val!=q.val){
        return false;
    }

    return isSameTree(p.left,q.left)&& isSameTree(p.right,q.right);

}

11非递归前中后序列

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    //线性表非递归前序遍历
    public List<Integer> preorderTraversal(TreeNode root) {
        // 存储遍历结果
        List<Integer> result = new ArrayList<>();
        // 用ArrayList模拟栈，存储TreeNode类型
        List<TreeNode> stack = new ArrayList<>();

        if (root == null) {
            return result;
        }

        TreeNode cur = root;

        while (cur != null || !stack.isEmpty()) {
            // 遍历左子树，先访问节点再入栈
            while (cur != null) {
                result.add(cur.val); // 将节点值加入结果列表
                stack.add(cur);      // 节点入栈
                cur = cur.left;      // 移动到左子节点
            }

            // 左子树遍历完毕，出栈
            cur = stack.remove(stack.size() - 1);
            // 转向右子树
            cur = cur.right;
        }

        return result;
    }
    //线性表非递归中序遍历
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if(root == null){
            return list;

        }
        TreeNode cur = root;
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){

                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            list.add(top.val);
            cur = top.right;
        }
        return list;
    }
    //线性表非递归后序遍历
    public List<Integer> postorderTraversal(TreeNode root){
        List<Integer> list = new ArrayList<>();
        if (root == null) {
            return list;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;
        while (cur!=null||!stack.isEmpty()){
            while (cur!=null){
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if(top.right==null||prev == top.right){
                list.add(top.val);
                prev = top;
                stack.pop();
            }else {
                cur = top.right;
            }

        }
        return list;
    }

}

12找两个结点的公共祖先

import java.util.Stack;

public class TreeNode2 {
    int val;
    TreeNode2 left;
    TreeNode2 right;

    TreeNode2(int x) {
        val = x;
    }


    class Solution {
        public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

            Stack<TreeNode> stackP = new Stack<>();
            Stack<TreeNode> stackQ = new Stack<>();
            getPath(root, p, stackP);
            getPath(root, q, stackQ);
            int size_P = stackP.size();
            int size_Q = stackQ.size();
            if (size_P > size_Q) {
                int count = size_P - size_Q;
                while (count != 0) {
                    stackP.pop();
                    count--;
                }
            } else {
                int count = size_Q - size_P;
                while (count != 0) {
                    stackQ.pop();
                    count--;
                }

            }
            while (!stackP.isEmpty() && !stackQ.isEmpty()) {
                if (stackP.peek() == stackQ.peek()) {
                    return stackP.peek();
                } else {
                    stackP.pop();
                    stackQ.pop();
                }
            }
            return null;

        }

        public boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
            if (root == null) {
                return false;
            }
            stack.push(root);
            if (root == node) {
                return true;
            }
            TreeNode cur = root;
            boolean ret = getPath(root.left, node, stack);
            if (ret) {
                return true;
            }
            ret = getPath(root.right, node, stack);
            if (ret) {
                return true;
            }
            stack.pop();
            return false;
        }
    }
}