信息、熵、信息增益、基尼指数

信息

信息是用来消除随机不确定性的东西，放在机器学习的语境里是这样的，每个类xi的信息为：

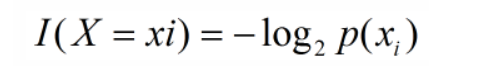
I表示信息，p(xi)表示指xi的概率

熵

熵是对随机变量不确定性的度量，是信息的期望值

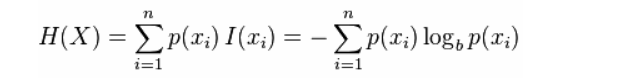
熵只依赖于随机变量的分布，和其取值没有关系
熵是用来度量不确定的，所以熵越大，X=xi的不确定性越大
给了样本集合D后，其经验熵为：

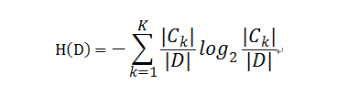
k表示有k个分类，|CK|为样本集中属于K类的样本数

条件熵

在一个条件下，随机变量的不确定性

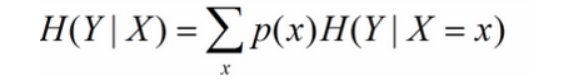
机器学习中可以理解为给定某个特征后的熵
比如在一个集合中，年龄特征下有青年、中年、老年三项，最后的分类分为是、否两类
那在年龄中==青年、中年、老年的情况下，在各自集合里都有样本属于是、否不同的类别
可以分贝算出H(Y|X=青年)、H(Y|X=中年)和H(Y|X=老年)，以及p(青年)、p(中年)、p(老年),相乘求和就可以计算在年龄条件下的条件熵

经验条件熵

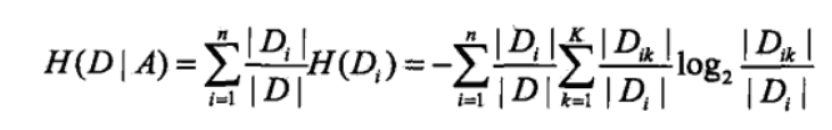
信息增益

熵 - 条件熵
信息增益可以作为决策树中用来选择特征的指标
由于 熵 是随机变量的不确定性， 条件熵是在某一条件下随机变量的不确定性，所以信息增益就是某一条件下随机变量不确定性减少的程度

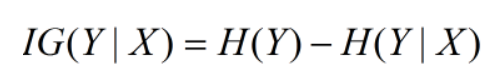
在决策树构建时，H(Y)表示划分前的熵，H(Y|X)表示划分后的条件熵，后者越小，说明在此条件下随机变量的不确定度越小，相应的信息增益越大，我们想要的正是随机变量的不确定性变小、纯度变高，也就是选择信息增益最大的，ID3算法中就以此为特征选择的方式（sklearn中决策树的critir参数为‘entropy’）

但是信息增益偏向取值较多的特征，要解决这个缺点可以用信息增益比

信息增益比

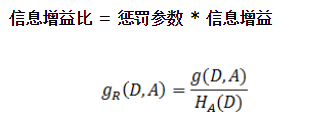
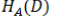就是上面在A条件下的熵

基尼指数

Gini系数是一种与信息熵类似的做特征选择的方式，可以用来数据的不纯度。在CART(Classification and Regression Tree)算法中利用基尼指数构造二叉决策树（选择基尼系数最小的特征及其对应的特征值）。
基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。
是sklearn决策树的默认选择标准

注意： Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。
基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

CART是个二叉树，也就是当使用某个特征划分样本集合只有两个集合：1. 等于给定的特征值 的样本集合D1 ， 2 不等于给定的特征值 的样本集合D2

实际上是对拥有多个取值的特征的二值处理。
某个特征划分后的Gini指数：
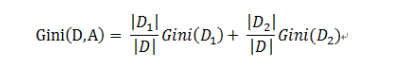(毕竟是二叉)
因而对于一个具有多个取值（超过2个）的特征，需要计算以每一个取值作为划分点，对样本D划分之后子集的纯度Gini(D,Ai)，(其中Ai 表示特征A的可能取值)

然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分，这个划分的划分点，便是使用特征A对样本集合D进行划分的最佳划分点。