Floyd-Warshall算法解决所有节点对最短路径问题

Floyd-Warshall算法解决所有节点对最短路径问题

在计算机科学中，解决图论中最重要的问题之一就是最短路径问题。其中，一种经典的算法是Floyd-Warshall算法，它能够有效地找到图中所有节点对之间的最短路径。无论是在网络路由、交通规划还是其他领域，Floyd-Warshall算法都具有广泛的应用价值。

算法原理

Floyd-Warshall算法采用动态规划的思想来解决所有节点对最短路径问题。它通过逐步优化节点之间的路径长度来找到最短路径。

算法的核心思想是利用一个二维数组dist来记录从节点i到节点j的最短路径长度。初始时，dist[i][j]等于节点i到节点j的直接距离（如果两节点之间有边相连），或者设为无穷大（如果两节点之间没有直接相连的边）。

然后，对于每一个中间节点k，算法尝试更新从节点i到节点j的最短路径长度。如果从节点i经过节点k再到节点j的路径长度小于直接从节点i到节点j的路径长度，则更新dist[i][j]为经过节点k的路径长度。通过这样的迭代，最终可以得到所有节点对之间的最短路径。

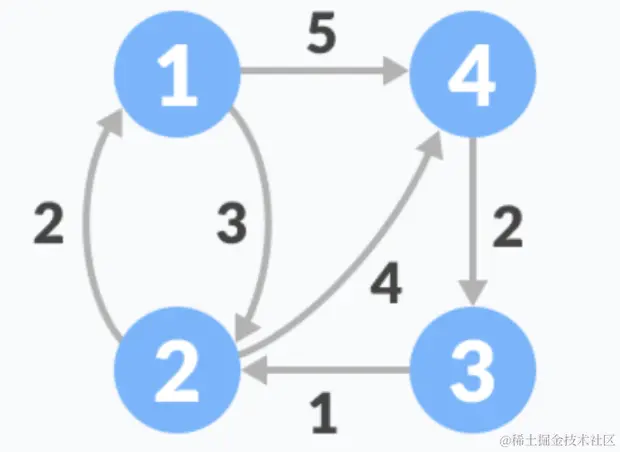
代码实现

下面是Floyd-Warshall算法的Python实现：

less

复制代码

def floyd_warshall(graph):    # 初始化距离矩阵    dist = [[float('inf') for _ in range(len(graph))] for _ in range(len(graph))]        # 初始化对角线上的距离为0    for i in range(len(graph)):        dist[i][i] = 0        # 根据图的邻接矩阵初始化距离矩阵    for i in range(len(graph)):        for j in range(len(graph)):            if graph[i][j] != 0:                dist[i][j] = graph[i][j]        # Floyd-Warshall算法核心部分    for k in range(len(graph