算法 | 如何通过Math.random()方法实现X平方或更多次方的概率？

前言

本文主要介绍Java中Math.random()方法以及该方法的简单应用。

每种语言都有随机方法，在Java中的随机方法有Math.random()方法、Random类。

Math.random

Math.random()方法的返回值的是double类型，其返回值的范围为[0,1)，包含0，不包含1，会把0 ~ 1之间的数进行等概率返回。

等概率验证

所说是等概率返回其中的某一个数，那我们能不能验证一下？

验证思路：

1. 设置一个循环，循环1千万次。
2. 定义一个变量count，用来记录这1千万次中，小于0.4的个数。
3. 在循环里判断如果返回值小于0.4，则count值加1。
4. 用count比上1千万，如果得出的值在0.4左右，说明是等概率的。

当然这个循环次数和0.4也可以是其他值。

来看下代码实现：

public class Code09_Random {

    public static void main(String[] args) {
        int times = 10000000;
        int count = 0;
        for (int i = 0; i < times; i++) {
            if (Math.random() < 0.4) {
                count++;
            }
        }

        System.out.println((double) count / (double) times);
    }
}
复制代码

经过多次执行验证结果如下：

当比较的数为0.4时，输出结果为0.4001569、0.3998326、0.3999383。

当比较的数为0.68时，输出结果为0.6799999、0.6800383、0.6800142。

当比较的数为0.8时，输出结果为0.7999352、0.800083、0.7999917。

等等，经过多次验证，发现比较值和输出的结果是非常接近的，这说明Math.random()是等概率返回的。

扩大范围

Math.random()返回值的范围为[0,1)，如果把Math.random()返回值乘以5，即Math.random() * 5，那么就可以得到[0,5)这个范围的数据，并且是等概率的，等概率验证方式与之前相同，不再赘述。

同样的，想要返回[0,K)之间的数，只需要乘以K即可，Math.random() * K，如果把得到的数据强转成int型，就可以得到[0,K-1]等概率数据。

Math.random()实现X2的概率

解析

Math.random()返回值的范围为[0,1)并且是等概率的，那么[0,X)上的数有X个，那么如果实现[0,X)范围的数据返回的概率为 X2 呢？

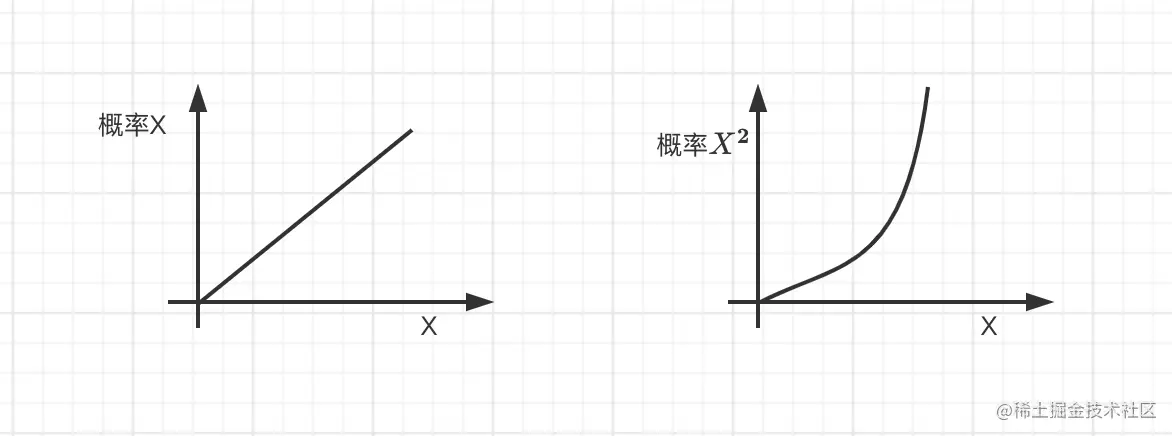
我们知道，在数学上，X和X2分别对应线性和曲线，对于X来说，[0, 0.3]出现的概率为0.3，[0, 0.8]出现的概率为0.8，[0, 1)出现的概率为1。

对于X2来说，X越小他对应的的概率越低，但是最终[0, 1)这个范围的概率是1。

代码实现

要实现这个功能，其实也很简单，调用两次Math.random()获取其最大值就可以了。

public static double x2Probability() {
    return Math.max(Math.random(), Math.random());
}
复制代码

嗯？是不是感觉很不可思议。下面我们来验证一下。

概率验证

验证思路也很简单，跟上面一样，定义一个count来记录一下，最后获取比例。怎么知道这个比例对不对呢？我们再获取目标概率的平方来对比下，如果两个值很接近的话，说明是对的。

public class Code10_Random {

    public static void main(String[] args) {
        int times = 10000000;
        int count = 0;
        double target = 0.4;
        for (int i = 0; i < times; i++) {
            if (x2Probability() < target) {
                count++;
            }
        }
        System.out.println((double) count / (double) times);
        System.out.println(Math.pow(target, 2));
    }

    public static double x2Probability() {
        return Math.max(Math.random(), Math.random());
    }
}
复制代码

多次执行结果如下：

# 0.4 对应的结果
0.1599787
0.16000000000000003
复制代码

# 0.8 对应的结果
0.6397657
0.6400000000000001
复制代码

实际测试的结果真的和X2的平方差不多。

原理解析

首先范围为[0,X)，x2Probability方法调用了2次Math.random()方法，并获取最大值，如果这个最大值落在[0,X)范围内，说明两次random产生的随机数，都落在了[0,X)范围内，概率自然是X2了。

当第一个Math.random()方法产生的随机数落在[0,X)范围内的概率为X，第二个Math.random()方法产生的随机数落在[0,X)范围内的概率也为X，两次随机事件是独立的，所以总概率为X2。

拓展

如果是想通过Math.random()实现X3的概率呢？和上面的原理是一样的，执行3次Math.random()方法即可，代码如下，验证方法和上面一致，就不再进行验证了。

public static double x3Probability() {
    return Math.max(Math.random(), Math.max(Math.random(), Math.random()));
}
复制代码

如果是想通过Math.random()实现XK的概率呢？同理，我们只需要调用K次Math.random()方法即可。