蒙特卡洛算法--三门问题、中奖概率

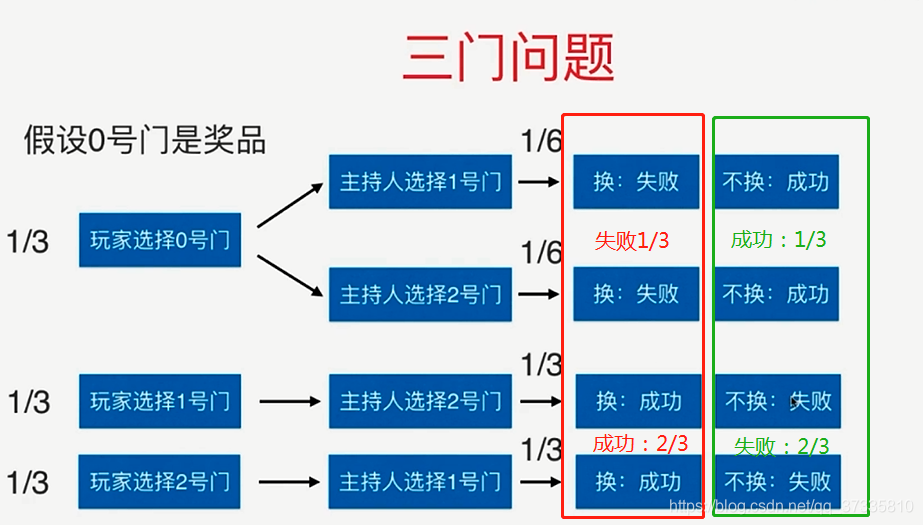
（一）三门问题：题目：https://baike.baidu.com/item/%E4%B8%89%E9%97%A8%E9%97%AE%E9%A2%98

结论先行：

换门-中奖概率：2/3；不换门-中将概率：1/3

代码

	private boolean play(boolean ChangeDoor){
		//Door:0,1,2
		int prizeDoor (int)(Math.random()*3);
		int playChoice = (int)(Math.random()*3);
		if (playChoice == prizeDoor)
			return ChangeDoor ? false : true;
		else
			return ChangeDoor ? true : false;

	}

 

 

（二）中奖问题：

题目：抽奖中，宝箱中奖概率是20%，抽5个能不能保证100%中奖？

结论：不能

解析：

中奖概率为20%，按照每次抽5个，在100万数据统计下，中奖率为0.67；（1-0.8^5 = 0.6723）

如果每次抽10个，同样数据统计下，中奖率为0.89;（1-0.8^10 = 0.8926）