题解——Noip2018普及组3摆渡车

题目在这里

感谢Green_Hand的题解让我这个25分的蒟蒻终于懂得了这一题

首先算法是dp，是个人都想的出来
f[i][j]表示第i个人等待时间为j的时候前i个人的最小等待时间（太强了）‘

j的取值范围？

由题可知，若车在人大附中停了m分钟，那么不如在到人大附中时先送走一批人（即便当时没人），所以停车时间T1<m

设一个人等到车从人民大学回来的时间为T2
因为车往返一次只需m分钟，所以T2<m

综上，一个人等车的时间

j=T1+T2<2m

该如何转移？

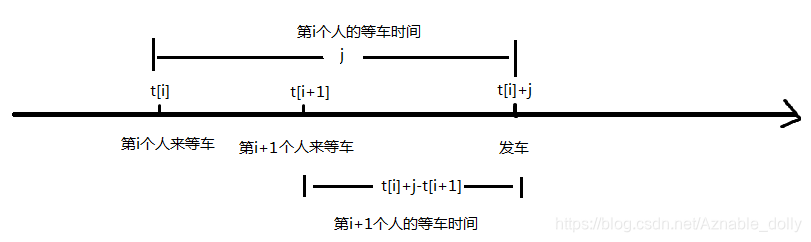
若下一个人能赶上当次车（即t[i]+j>=t[i+1]), 则将f[i][j]+t[i]+j-t[i+1]转移至f[i+1][t[i]+j-t[i+1]];

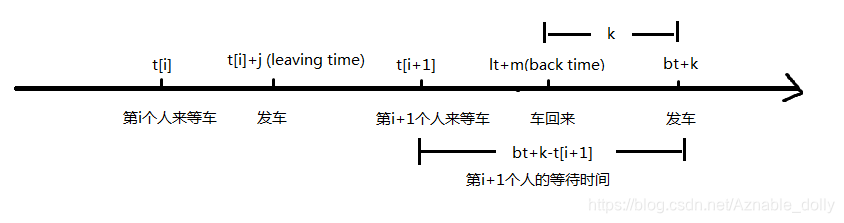
若下一个人在当次车回来之前开始等车（即t[i]+j+m>=t[i+1])， 则枚举车回来后停的时间k, 用f[i][j]+t[i]+j+m+k-t[i+1]转移f[i+1][t[i]+j+m+k-t[i+1]];

若下一个人在当次车回来之后才到（即t[i]+j+m<t[i+1]),则枚举下 一个人等待的时间k，并用f[