leetcode【数据结构简介】《二叉树》卡片——总结

Authur Whywait 做一块努力吸收知识的海绵
想看博主的其他所有leetcode卡片学习笔记链接？传送门点这儿

从中序和后序遍历序列构造二叉树🚩

根据一棵树的中序遍历与后序遍历构造二叉树。、

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下二叉树

分析

首先我们要从中序遍历和后序遍历得到的两个序列inordor和postorder入手。仔细观察我们可以发现postorder的最后一个元素为根节点，然后确定根节点之后，可以在inorder中找到根节点，其左边部分是其左子树里的结点，右边部分是其右子树里的结点。如果不是很清楚，没关系，下面将给出手绘图助你更好理解。

我们就如下例子展开分析：

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

在确定左子树部分和右子树部分之后，我们把相应的参数传回去就可以完成一次次的递归啦。

步骤

如果中序遍历序列（后序遍历序列）为空，则返回NULL；
给结点分配空间，并为结点的 val 赋值；
找到结点在中序遍历序列中的索引；
将中序遍历序列 结点 左边部分序列 以及 后序遍历序列相应部分序列传入 builtTree 函数，并赋值给结点的 left 指针；
将中序遍历序列 结点 右边部分序列 以及 后序遍历序列相应部分序列传入 builtTree 函数，并赋值给结点的 right 指针。

代码实现以及执行结果

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize){

    if(inorderSize<=0) return NULL;

    struct TreeNode* s = (struct TreeNode *) malloc (sizeof(struct TreeNode));
    s->val = postorder[postorderSize-1];

    int pos;
    for(pos=0; pos<inorderSize; pos++)
        if(inorder[pos]==postorder[postorderSize-1]) break;

    s->left = buildTree(inorder, pos, postorder, pos);
    s->right = buildTree(inorder+pos+1, inorderSize-pos-1, postorder+pos, postorderSize-pos-1);

    return s;
}

从中序与后序遍历序列构造二叉树🚩

根据一棵树的前序遍历与中序遍历构造二叉树。

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下二叉树：

分析 & 步骤

思路和具体实现步骤，同上一个编程题几乎完全一样。

代码实现以及执行结果

struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    if(!preorderSize) return NULL;

    struct TreeNode* root = (struct TreeNode *) malloc (sizeof(struct TreeNode));
    root->val = preorder[0];

    int pos=0;
    while(inorder[pos]!=root->val) pos++;

    root->left = buildTree(preorder+1, pos, inorder, pos);
    root->right = buildTree(preorder+1+pos, preorderSize-1-pos, inorder+pos+1, inorderSize-1-pos);

    return root;
}

填充每个节点的下一个右侧节点指针🚩

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

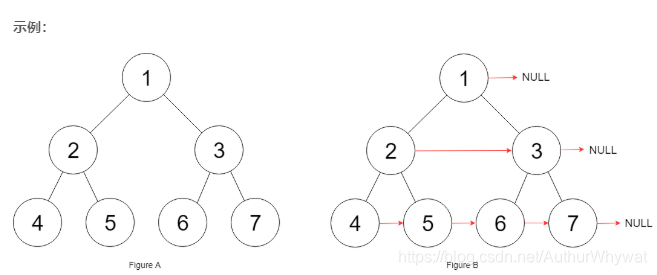
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

分析

看完题目，第一个联想到的就是之前经历过的一个练习 - 二叉树的层序遍历。

同样的想法，我们只要入列的时候将同一深度的结点用next串起来即可。

但是，如果要用递归算法，我们应该怎么做呢？

下面是递归算法的思路动态图：

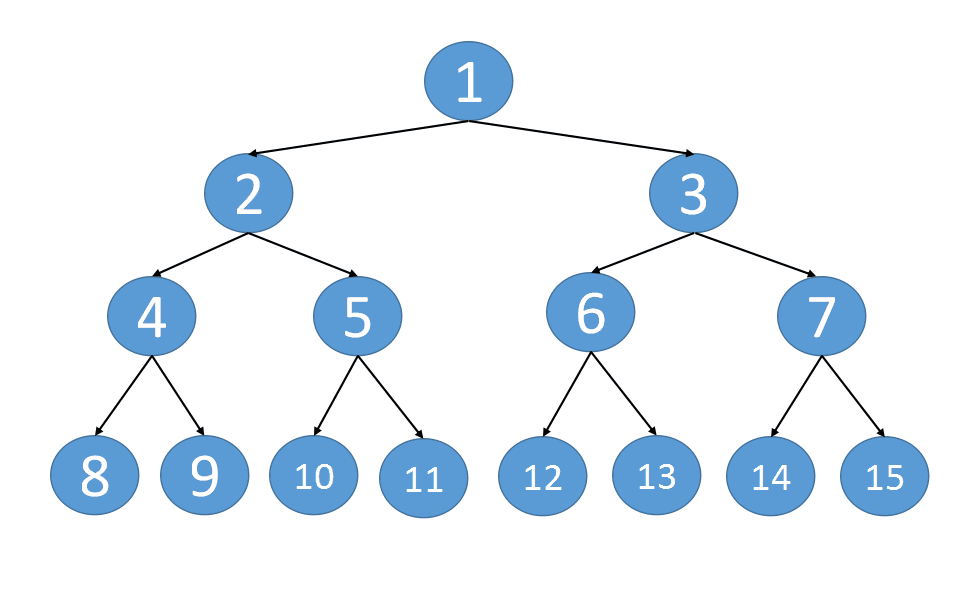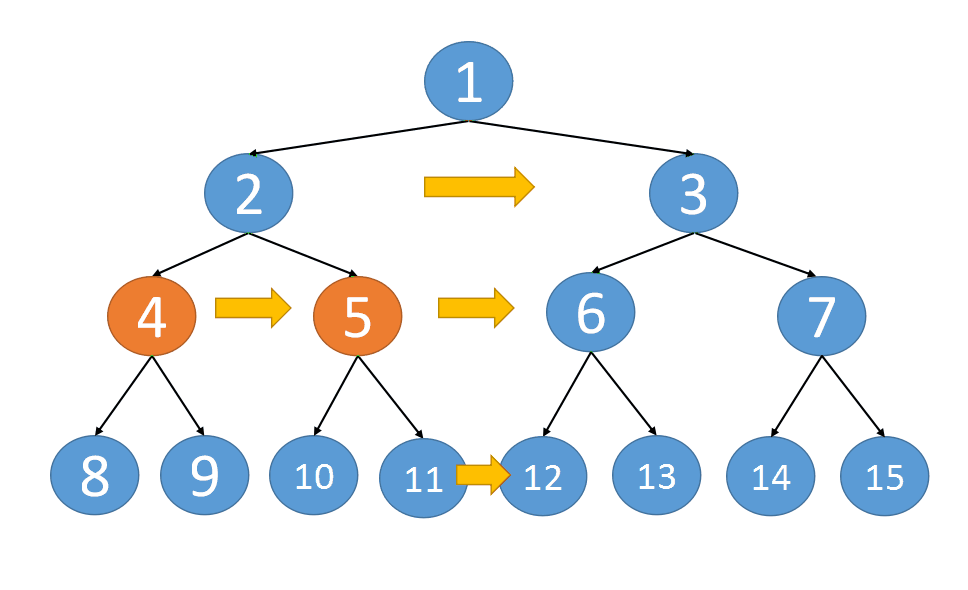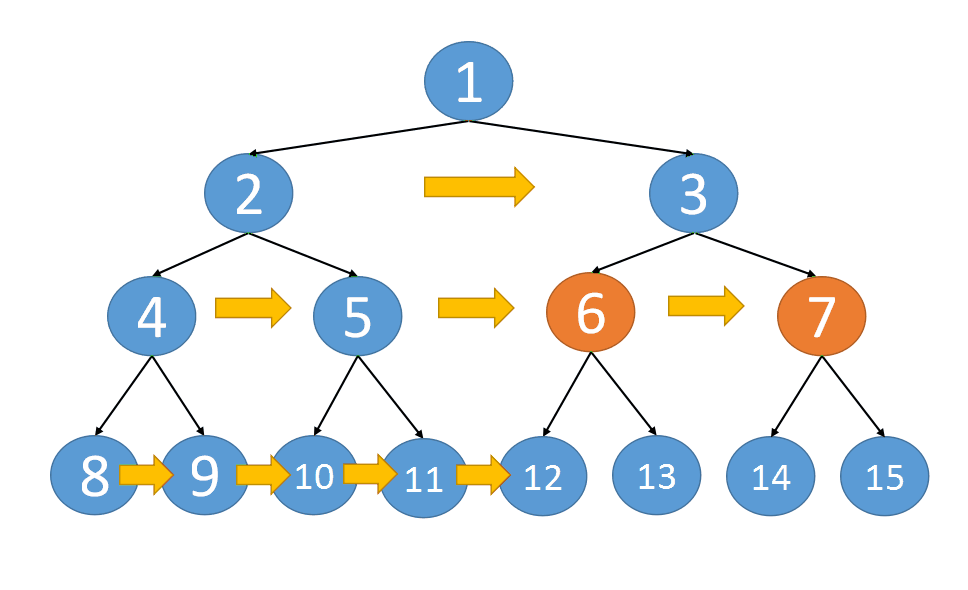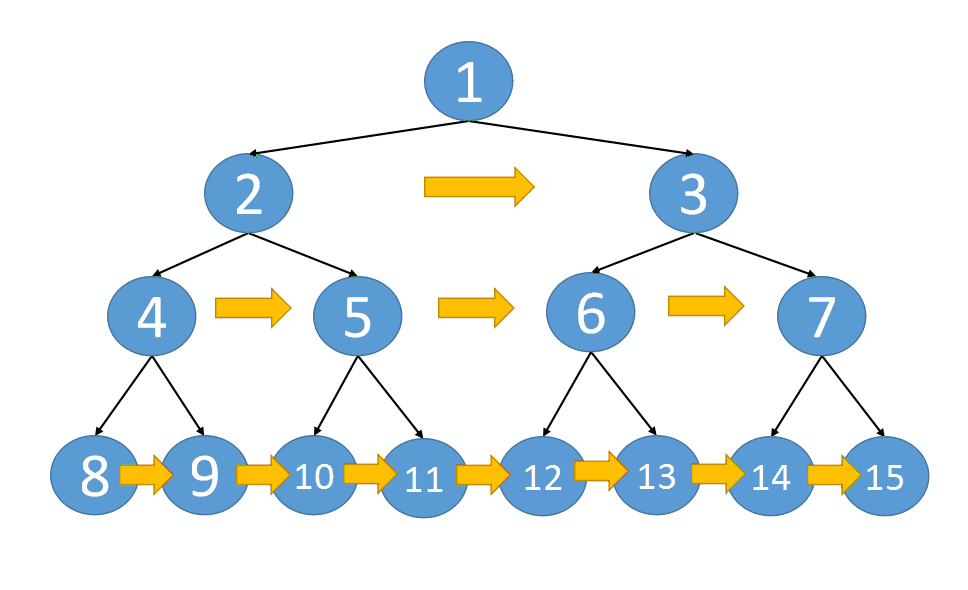
代码实现以及执行结果

struct Node* connect(struct Node* root) {
	if(!root || !root->left) return root;
    struct Node* leftpart = root->left, * rightpart = root->right;
    while(leftpart){
        leftpart->next = rightpart;
        leftpart = leftpart->right;
        rightpart = rightpart->left;
    }
    root->left = connect(root->left);
    root->right = connect(root->right);
    return root;
}

填充每个节点的下一个右侧节点指针 II🚩

给定一个二叉树

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]

分析

在上个程序中，我们使用的主要想法还是从图中观察出来的性质。那么这道题作为上一道题目的升级版，能否用一样的方法来完成呢？

struct Node* connect(struct Node* root) {
	if(!root) return root;
    struct Node* leftpart = root->left, * rightpart = root->right;
    while(leftpart && rightpart){
        leftpart->next = rightpart;

        if(leftpart->right) leftpart = leftpart->right;
        else leftpart = leftpart->left;

        if(rightpart->left) rightpart = rightpart->left;
        else rightpart = rightpart->right;
    }

    root->left = connect(root->left);
    root->right = connect(root->right);

    return root;
}

我对之前的程序做了一些修改，将在完全树中的"左半部分一直往右子树走，右半部分一直往左子树走"改成了，如果"左半部分如果有右子树那就一直往右子树走，否则走左子树；右半部分如果左子树那就一直往左子树走，否则走右子树"，这种策略可以避开null的结点，使得同一层的邻近两个都能连上。

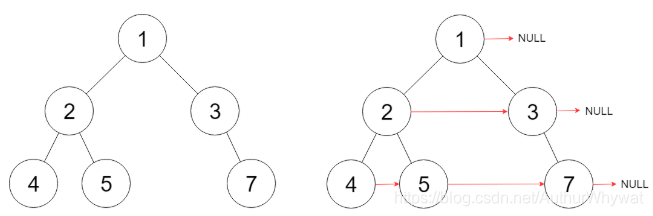
一切看起来都是那么完美无瑕，直到我遇到了下面这个测试用例：

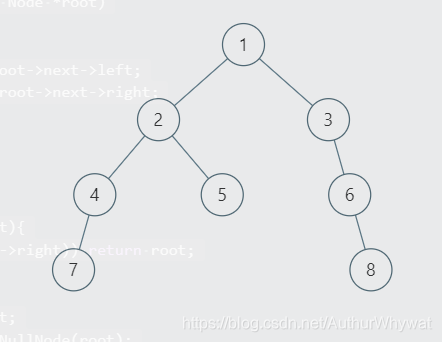
结点7的next应该为结点8的地址，但是按照我们前面的方法，并没有使得结点7的next指针指向结点8。

为什么呢？

因为在root为结点1的时候，以2为“代表”的左边部分，优先选择了走右子树方向到了结点5，而在结点5的next指针指向结点6之后while循环终止。递归算法实际走到root为结点2的时候，将结点4的next指针指向结点5之后，就不再有对next的写入了。

至于结点7的next指针指向结点8？不存在的。

这样子看来，我们的思维走到了一个死胡同。

等等等等（其实这是个拟声词），下面将介绍一种新的方法：妙用 next 指针。

思路

从上往下，一层层完善next指针。

通过上一层结点的next指针，去寻找同一层右边结点中最近的结点。

动态演示如下：

（一笔笔画，一帧帧截图，然后拼起来做成gif，确实挺麻烦的。如果这动态图对你理解有帮助，请务必点个赞👍）

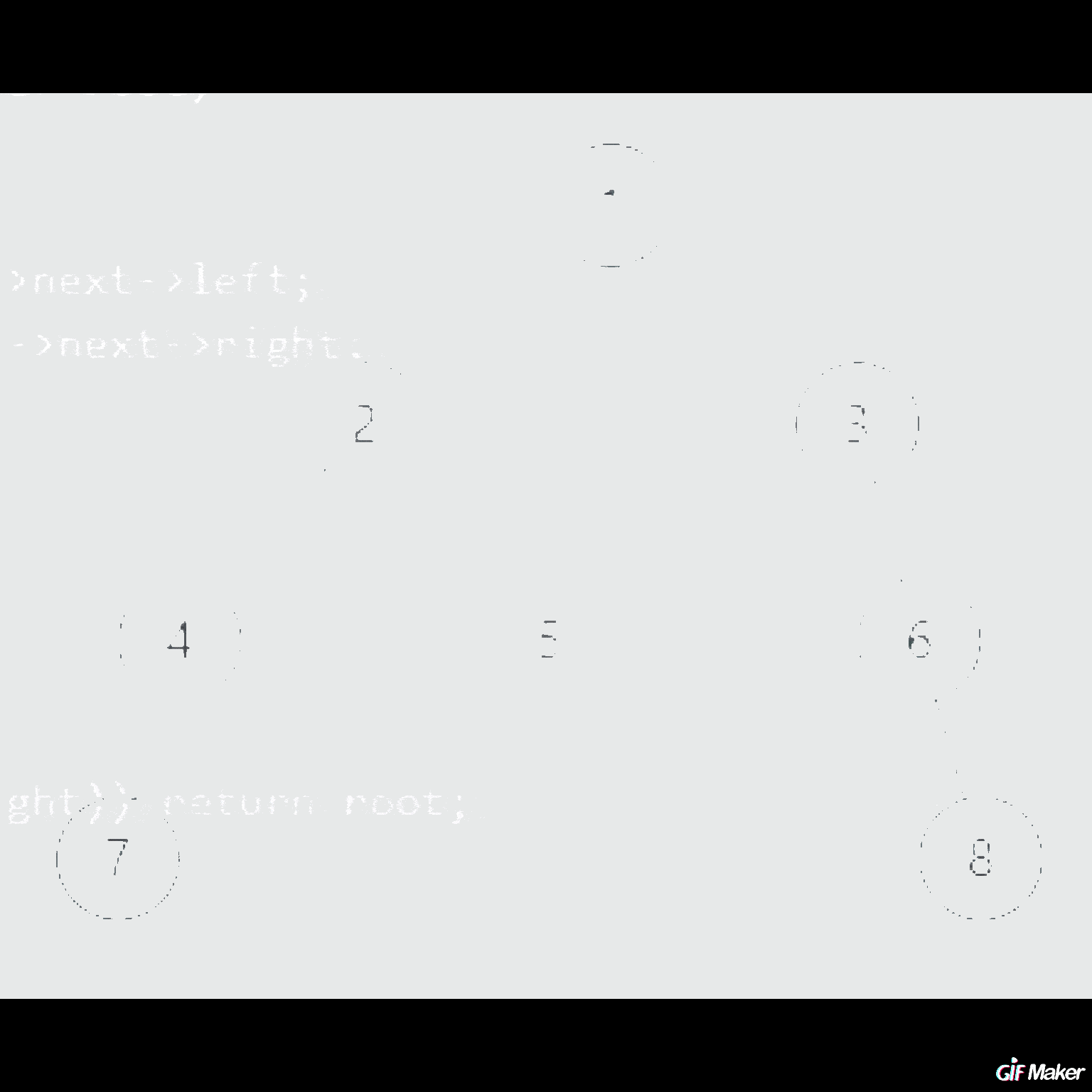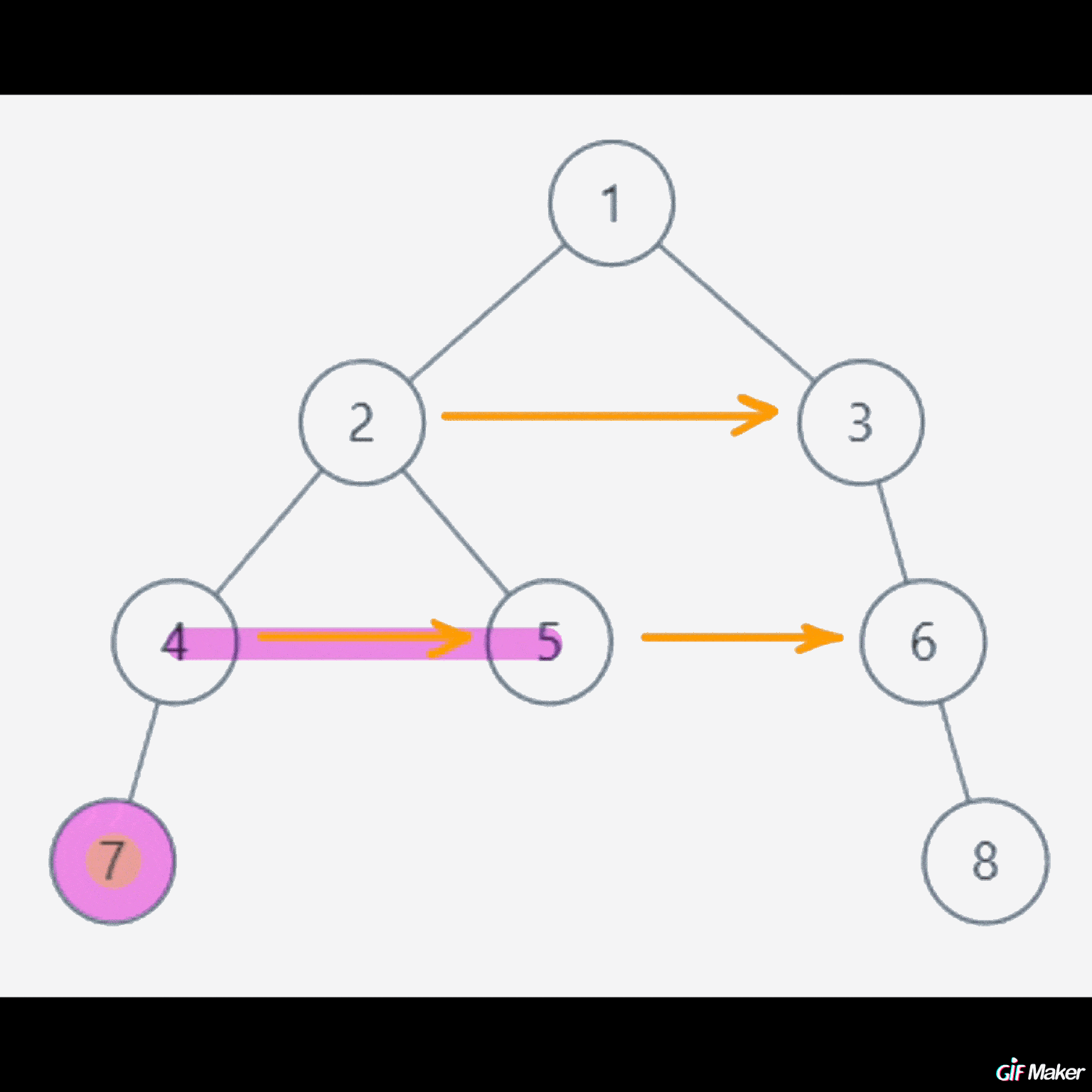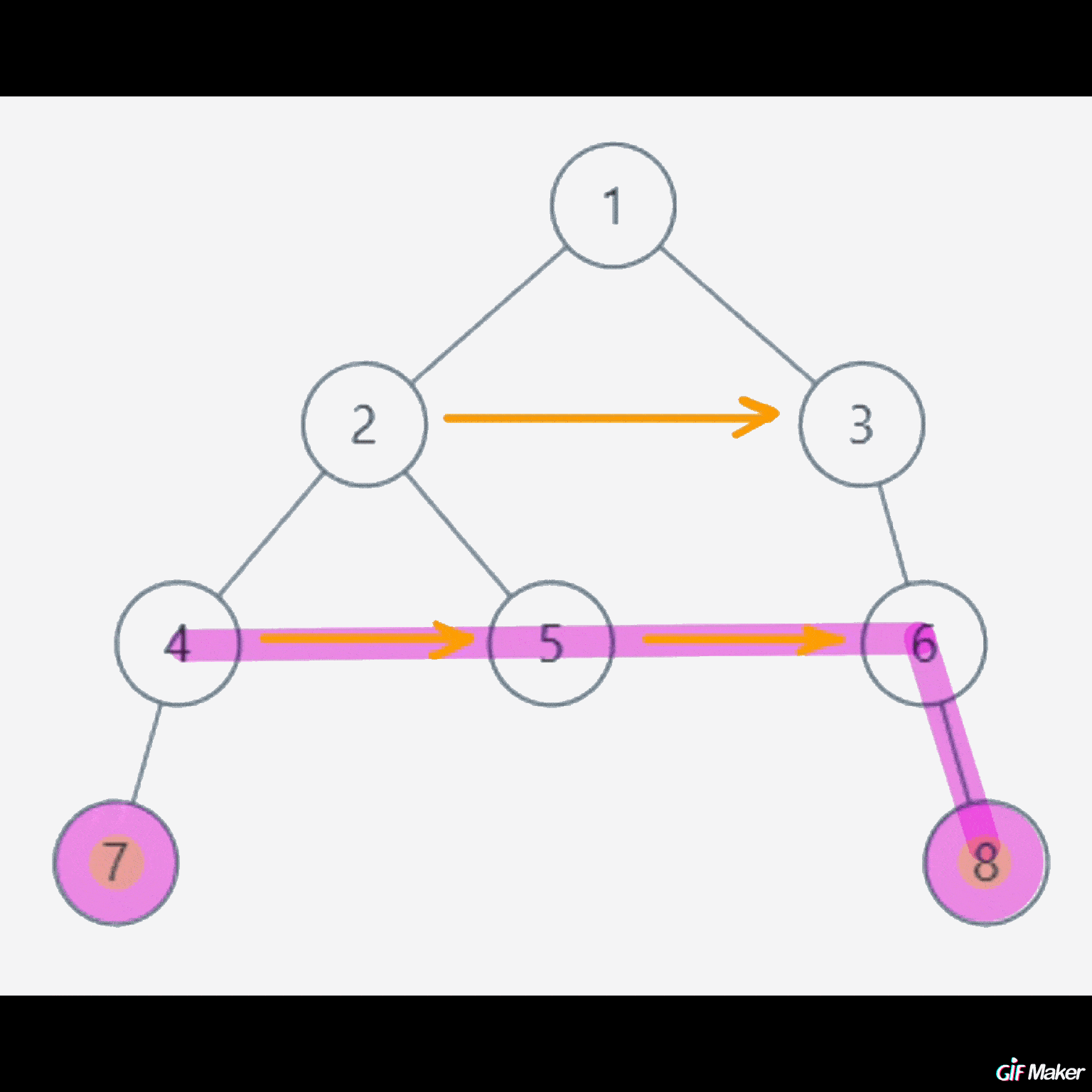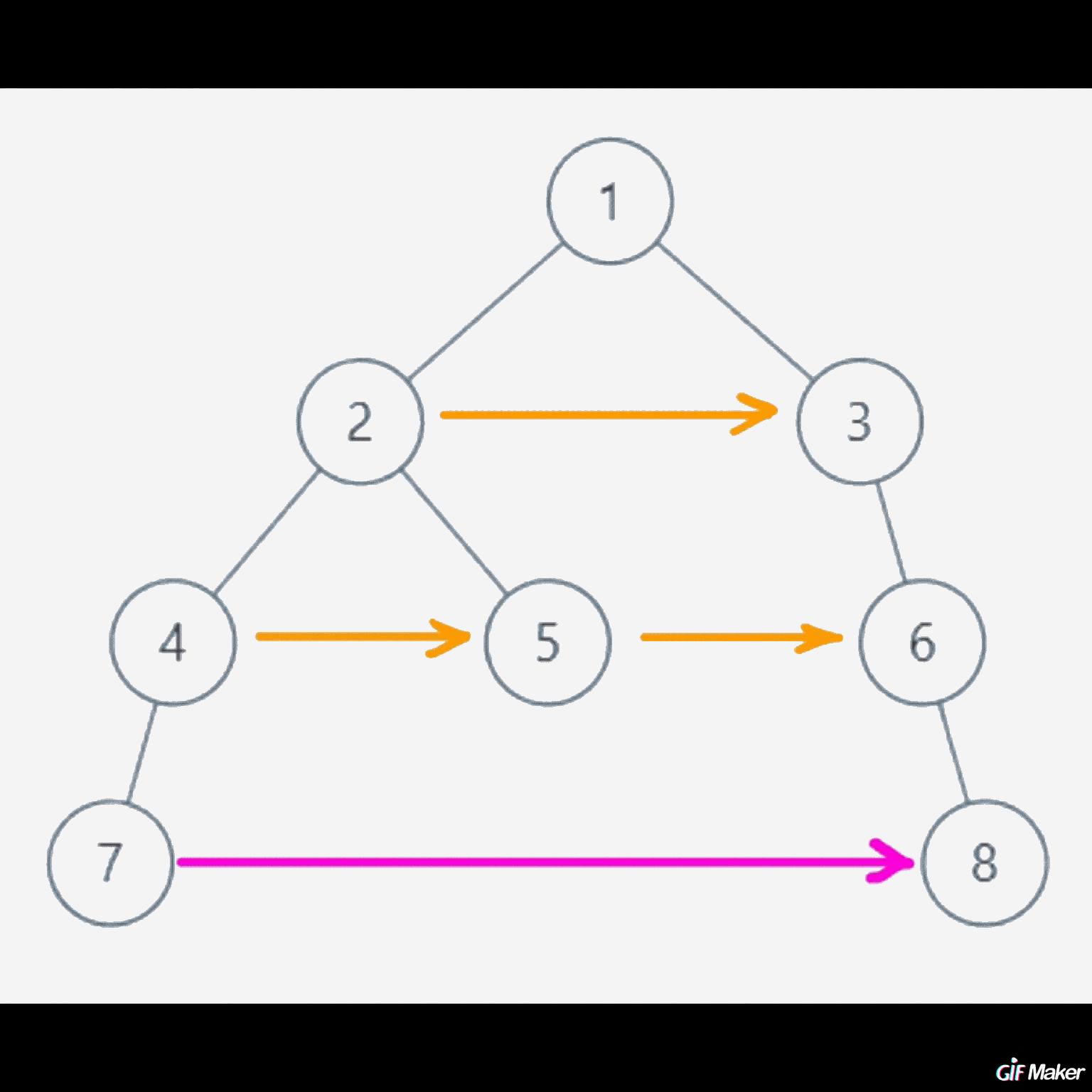
代码实现以及执行结果

struct Node *GetNextNoNullNode(struct Node *root)
{
    while(root->next){
        if(root->next->left) return root->next->left;
        if(root->next->right) return root->next->right;
        root = root->next;
    }
    return NULL;
}

struct Node *connect(struct Node *root){
    if(!root || (!root->left && !root->right)) return root;

    if(root->left && root->right){
        root->left->next = root->right;
        root->right->next = GetNextNoNullNode(root);
    } 
    else if(root->left) root->left->next = GetNextNoNullNode(root);
    else if(root->right) root->right->next = GetNextNoNullNode(root);

    root->right = connect(root->right);
    root->left = connect(root->left);

    return root;
}

二叉树的最近公共祖先🚩

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

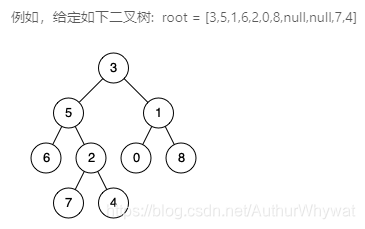
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

分析

自从开始动态图制作后，我发现没有什么是比动态图说的更清楚的。所以，虽然很麻烦，但是还是把动态图做出来啦。

不过因为刚开始接触，所以动态图都有这样子或者那样的瑕疵，见谅。

我们分析用的还是上面那张图，要找的是结点6和结点4的最近公共祖先。

四种情况：

1. 如果root为p或者q或者空，直接返回root；
2. 如果left为空而right不为空，则返回right；
3. 如果right为空而left不为空，则返回left；
4. 如果left和right都不为空，则返回root（说明root为找到的祖宗）。

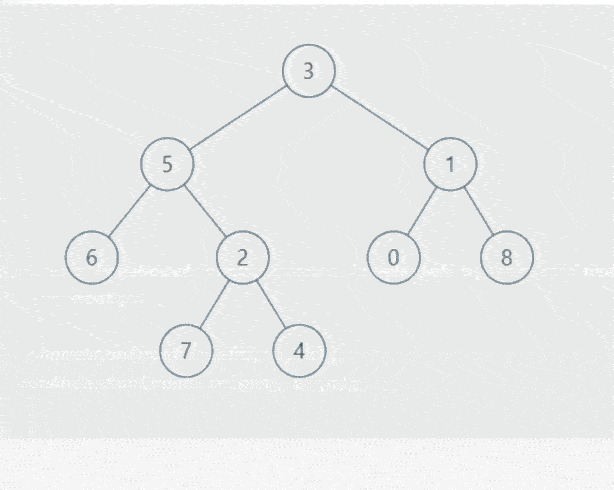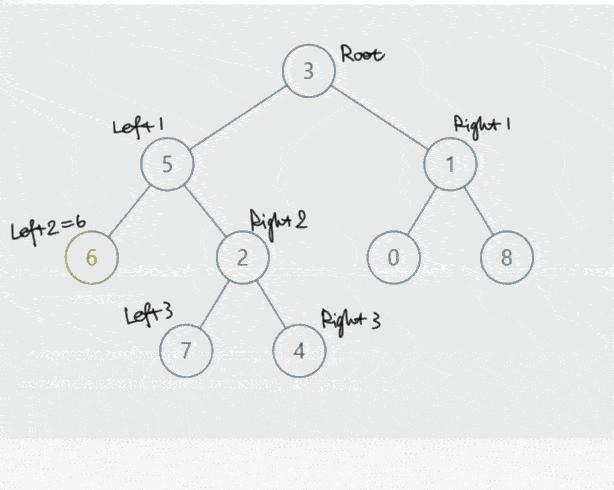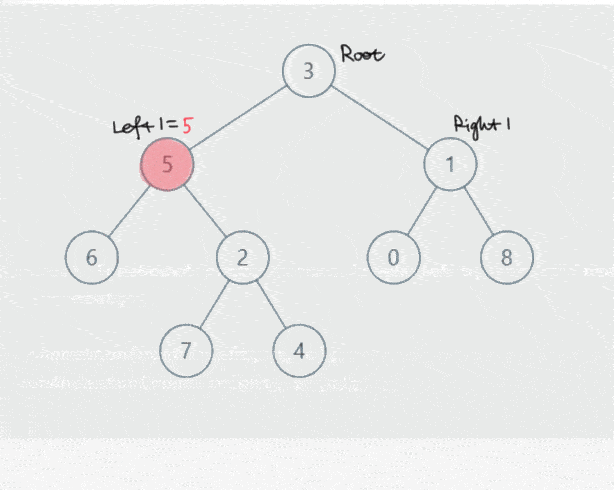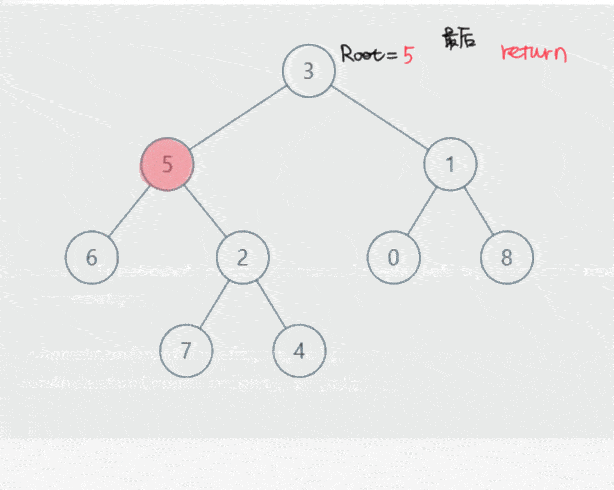
很奇怪的就是本来淡黄色的标记没有了。。。

代码实现以及执行结果

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) {
    if(!root || root==p || root==q) return root;
    
    struct TreeNode* left = lowestCommonAncestor(root->left, p, q);
    struct TreeNode* right = lowestCommonAncestor(root->right, p ,q);

    if(!left && !right) return NULL;
    else if(left && !right) return left;
    else if(right && !left) return right;
    else return root;
}

二叉树的序列化与反序列化🚩

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

大道至简法（师承此处）

/** Encodes a tree to a single string. */
char* serialize(struct TreeNode* root) {
    return  (char *)root;
}

/** Decodes your encoded data to tree. */
struct TreeNode* deserialize(char* data) {
    return (struct TreeNode *)data;
}

都看到这儿了，不点个赞再走么(ノ｀Д)ノ