微分流形（一）：什么是微分流形

一、简介 

目录

一、简介 

二、一维流形

三、二维流形

        流形（manifold）是数学中描述“弯曲空间”的概念：它在局部（每一点附近）看起来像平坦的欧几里得空间，但整体上可能弯曲或复杂。按我的理解就是流形是一种工具，是光滑曲面的一系列局部映射簇，而且满足以下性质：单射满射且光滑，反函数同理。

二、一维流形

一维流形就像一条“线”或“曲线”,局部参数化可定义一维流形，如以下例子

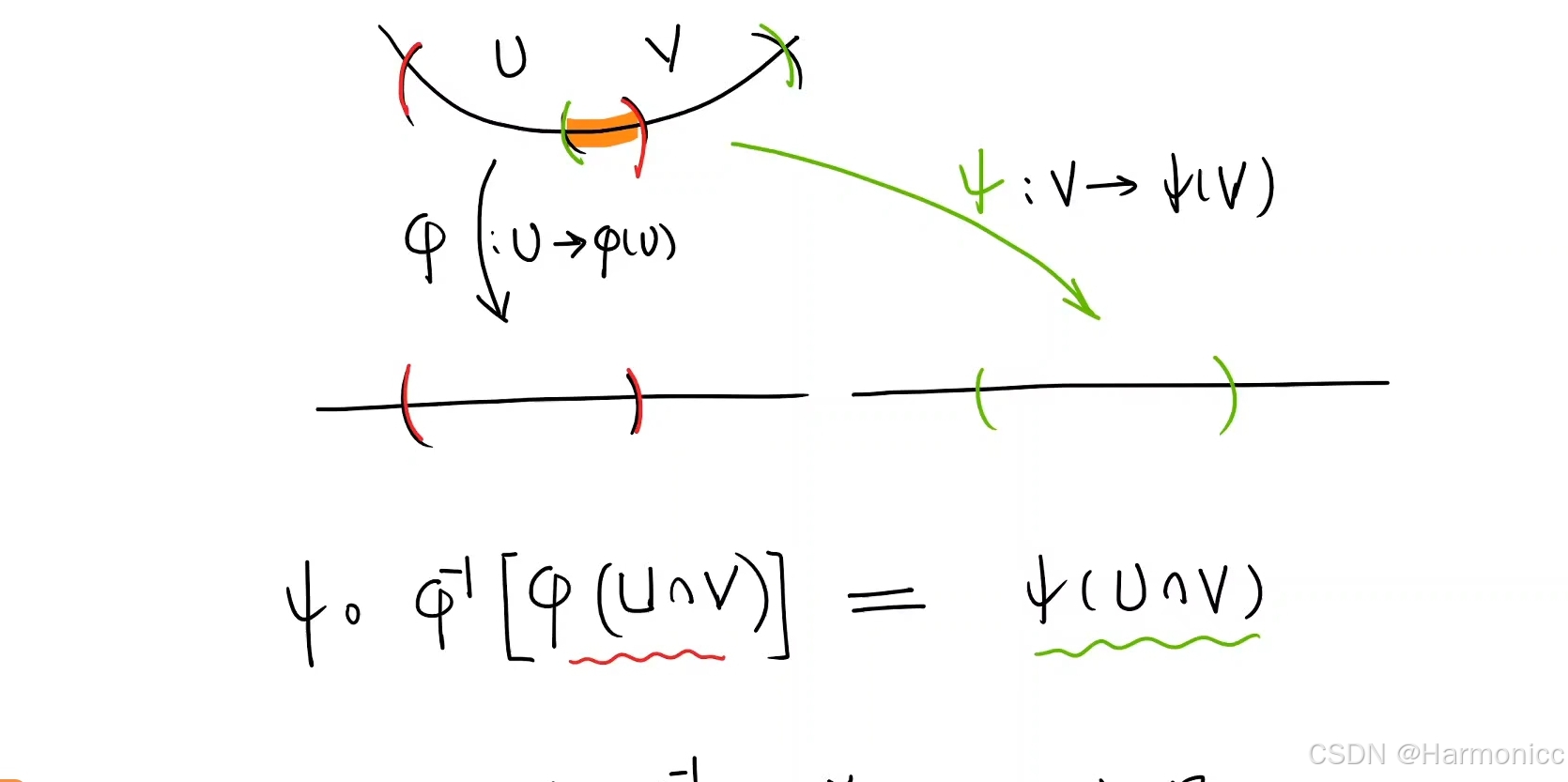
曲线分为红色部分及绿色部分以及它们的交集，计,可建立实数到实数的映射，最后一部分可以这样理解

简单来说就是同一段曲线可以有不同的参数表示。

三、二维流形

可以从一维流形推广，二维流形就像一个“曲面”，不妨记集合为二维流形，这里对孙健老师的笔记作如下解释

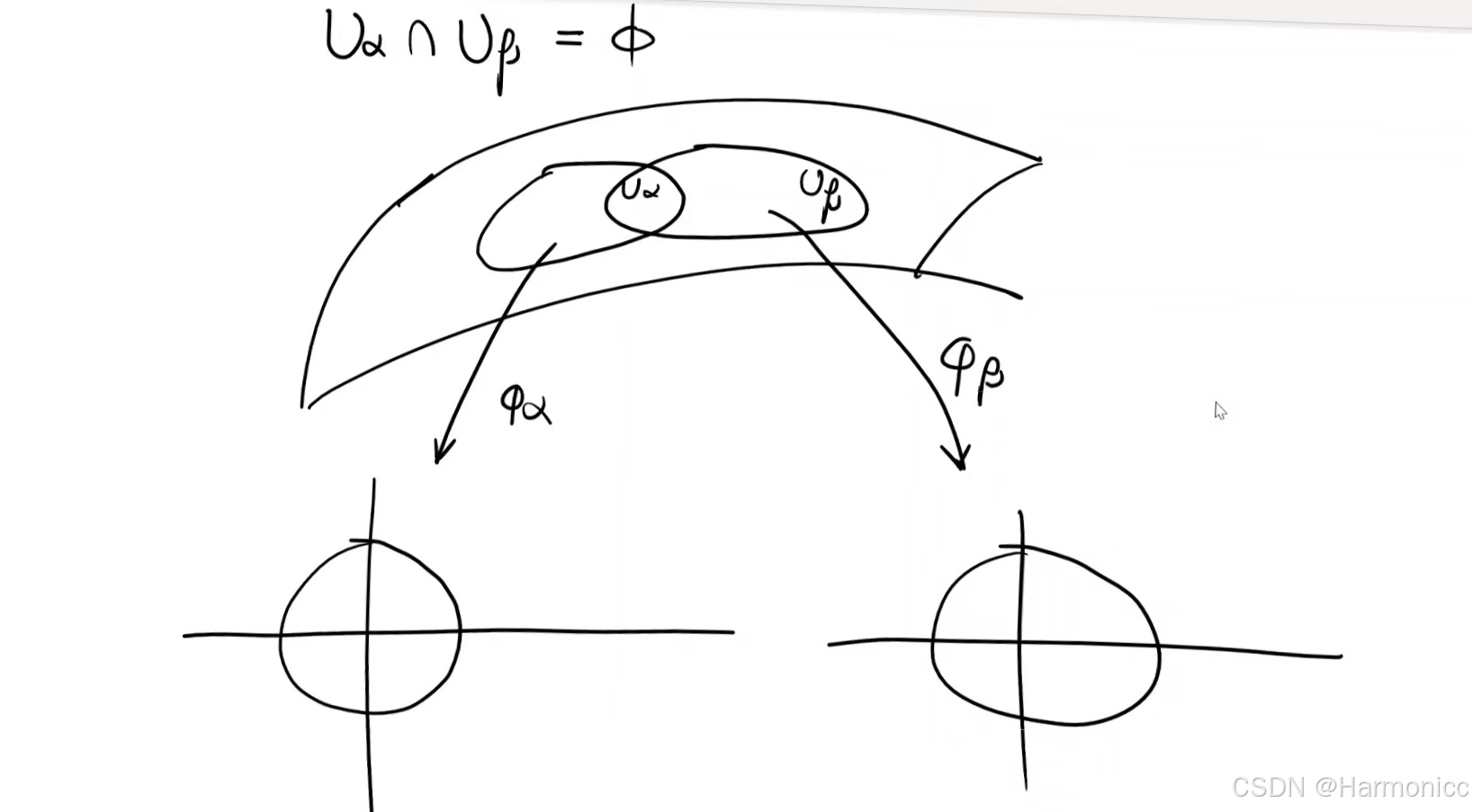
第一小节结束。

需要说明的是，这系列笔记自用，隐去了这门课程的大量严肃数学细节，如Hausdorff、second-countable，后面的笔记作相同处理。