算法编程的一些注意点

一、栈与队列

1、
INT_MAX = 2^31 - 1 =2147483647，INT_MIN= - 2^31 = -2147483648
INT_MIN需定义成 -INT_MAX - 1, 因为-2147483648无法表示, 无法对2147483648取反

INT_MAX + 1 = INT_MIN
INT_MIN - 1 = INT_MAX
abs(INT_MIN) = INT_MIN (INT_MAX溢出)

在C/C++语言中，不能够直接使用-2147483648来代替最小负数，因为这不是一个数字，而是一个表达式。表达式的意思是对整数21473648取负，但是2147483648已经溢出了int的上限，所以定义为
(-INT_MAX -1)。
2、
leecode调用系统函数min等函数加作用域std::min(a,b)
stack里面没有元素时，调用 sta.top() 会报错
3、
辅助栈的作用

二、 链表

1、反转链表并输出反转后的头节点，
new一个结构体指针的方式

	// Definition for a Node.
	class Node {
	public:
	    int val;
	    Node* next;
	    Node(int  _val) {
	        val =  _val;
	        next = NULL;
	    }
	};

2、当需要复制一个链表的时候：
在主程序中初始化这个结构体，用深拷贝的方式，避免重复释放内存，new一段内存去存放新的结构体指针，初始化一个空节点 dum ： Node *dum=new node(0); 而深拷贝一个结构体指针指向的链表：Node *node=new Node(cur->val)

class Solution {
public:
    Node* copyRandomList(Node* head) {
        Node* cur = head;
        Node* dum = new Node(0), *pre = dum;
        while(cur != nullptr) {
            Node* node = new Node(cur->val); // 复制节点 cur
            pre->next = node;                // 新链表的 前驱节点 -> 当前节点
            cur = cur->next;                 // 遍历下一节点
            pre = node;                      // 保存当前新节点
        }
        return dum->next;
    }
};

关于初始化一个结构体指针的注释：

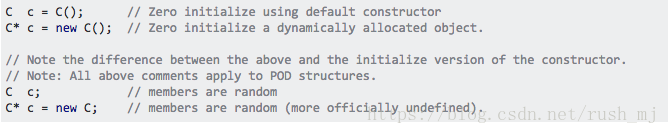
3、如果需要在复制的链表中加入指向任意节点的指针，那可以用哈希表的思想实现，map结构会按照键值自动排序，所以使用如下：

C++ STL 标准库中提供有 4 种无序关联式容器， unordered_map 容器。

unordered_map 容器，直译过来就是"无序 map 容器"的意思。所谓“无序”，指的是 unordered_map 容器不会像 map 容器那样对存储的数据进行排序。换句话说，unordered_map 容器和 map 容器仅有一点不同，即 map 容器中存储的数据是有序的，而 unordered_map 容器中是无序的。
对于已经学过 map 容器的读者，可以将 unordered_map 容器等价为无序的 map 容器。

具体来讲，unordered_map 容器和 map 容器一样，以键值对（pair类型）的形式存储数据，存储的各个键值对的键互不相同且不允许被修改。但由于 unordered_map 容器底层采用的是哈希表存储结构，该结构本身不具有对数据的排序功能，所以此容器内部不会自行对存储的键值对进行排序。

值得一提的是，unordered_map 容器在<unordered_map>头文件中，并位于 std 命名空间中。因此，如果想使用该容器，代码中应包含如下语句：

   #include <unordered_map>
	using namespace std;

unordered_map 容器模板的定义如下所示：

template < class Key,                        //键值对中键的类型
           class T,                          //键值对中值的类型
           class Hash = hash<Key>,           //容器内部存储键值对所用的哈希函数
           class Pred = equal_to<Key>,       //判断各个键值对键相同的规则
           class Alloc = allocator< pair<const Key,T> >  // 指定分配器对象的类型
           > class unordered_map;

以上 5 个参数中，必须显式给前 2 个参数传值，并且除特殊情况外，最多只需要使用前 4 个参数，如何去使用尼，参考创建C++ unordered_map容器的方法
例如：1) 通过调用 unordered_map 模板类的默认构造函数，可以创建空的 unordered_map 容器。比如：

std::unordered_map<std::string, std::string> umap;

由此，就创建好了一个可存储 <string,string> 类型键值对的 unordered_map 容器
注：map类型的赋值时，指定对组的形式来初始化：map[cur]=123;就是cur只想到额值是123

三、字符串

1、char& operator[](int n); //通过[]方式取字符；char& at(int n); //通过at方法获取字符

在进行替换字符串中某个字符串时，要先扩展字符串的长度，以NULL/0填充，然后用两个指针去从尾部遍历，遇到不替换的，复制，遇到要替换的，替换

str.insert(1, “111”);
str.erase(1, 3); //从1号位置开始3个字符

void test01()
{
string str = "hello world";
for (int i = 0; i < str.size(); i++)
{
cout << str[i] << " ";
}
cout << endl;
for (int i = 0; i < str.size(); i++)
{
cout << str.at(i) << " ";
}
cout << endl;
//字符修改
str[0] = 'x';
str.at(1) = 'x';
cout << str << endl;
}
int main() {
test01();
system("pause");
return 0;
}

2、

/字符串插入和删除
void test01()
{
string str = "hello";
str.insert(1, "111");
cout << str << endl;
str.erase(1, 3); //从1号位置开始3个字符
cout << str << endl;
}
int main() {
test01();
system("pause");
return 0;
}

3、string substr(int pos = 0, int n = npos) const; //返回由pos开始的n个字符组成的字符串

四、容器

1、vector支持随机访问，因此 vector 的insert（const_iterator pos,ele），可以在任意位置插入元素，在指针指向的位置指向的位置插入元素，比如

v2.insert(v2.begin()+4, L"3");   //在指定位置，例如在第五个元素前插入一个元素

2、删除任意位置的某个元素，erase，某个区间可以指定为1

   v2.erase(v2.begin()); //删除开头的元素
   v2.erase(v2.begin(),v2.end); //删除[begin,end]区间的元素
   v2.pop_back();   //删除最后一个元素

3、当然也可以常规push_back() pop_back()
4、swap可以使两个容器互换，可以达到实用的收缩内存效果，当 v 的容量大于size的时候，重新指定 v.resize()，然后用swap去交换指定后存在内存冗余的 v 和指定前的 v

vector<int>(v).swap(v); //匿名对象

4、size是真实元素的所占的空间打开，capacity是整个可容纳的空间大小
5、重新分配空间=来一次拷贝 resize( )函数
6、*****创建二维数组的方法：
① 默认初始化，vector 为空， size 为0。容器中没有元素，而且 capacity 也返回 0，意味着还没有分配内存空间。这种初始化方式适用于元素个数未知，需要在程序中动态添加的情况。

vector<int> list1;

② 拷贝构造
以下两种方式等价 ，list2 初始化为 list 的拷贝。list 必须与 list2 类型相同，也就是同为 int 的 vector 类型，list2 将具有和 list 相同的容量和元素。

	   vector<int> list2(list);
	   vector<int> list2 = list;

③ 直接赋值

       vector<int> list = {1,2,3.0,4,5,6,7};
       vector<int> list3 {1,2,3.0,4,5,6,7}; 

④ list3 初始化为两个迭代器指定范围中元素的拷贝，范围中的元素类型必须与 list3 的元素类型相容。

	vector<int> list3(list.begin() + 2, list.end() - 1);
注意：由于只要求范围中的元素类型与待初始化的容器的元素类型相容，因此迭代器来自不同的容器是可能的，例如，用一个 double 的 list 的范围来初始化 list3 是可行的。

⑤ 默认值初始化，list 中将包含7个元素，每个元素进行缺省的值初始化。对于int，也就是被赋值为0，因此 list4 被初始化为包含7个0。当程序运行初期元素大致数量可预知，而元素的值需要动态获取的时候，可采用这种初始化方式。

	vector<int> ilist4(7);

⑥ 指定值初始化，ilist5被初始化为包含7个值为3的int。

	vector<int> ilist5(7, 3)

⑦ 做题的时候 需要自己 cin 二维数组：需要自己制定长宽。选择以上方式创建

法一：一维扩充
		vector<vector<int>>vec(N);
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < M; j++) {
				vec[ i ].resize(M);
				cin >> num;
				vec[ i ] [ j ] = num;
			}
		} 
		
 法二：先创建 一维 vector<int>v1  然后外层 vector<vector<int>>vec ;  vec.push_back( v1 );

---

1、deque内部有一个map指针，deque重新分配空间速度比vector快，不需要拷贝原元素
2、支持insert的STL，vector deque list set map string
insert(pos,elem);//在pos位置插elem元素的拷贝，返回新数据的地址。
map和set由于插入后会自动排序，所以直接insert(ele)
3、set 和map内部都是 红黑树（自平衡二叉树）
4、支持 find() 函数的容器 set map unordered_map mutimap
5、map set 插入元素 只能用 insert() list 除了insert() 还可以链表前后操作 push_back() push_front()
----------------------------------------------------------
1、substr()这个获取子串的函数，函数的属性：开始位置，长度；
string substr(int pos = 0, int n = npos) const; //返回由pos开始的n个字符组成的字符串
////////// 太容易出错了
2、c++之to_string()函数

函数原型：
string to_string (int val);
string to_string (long val);
string to_string (long long val);
string to_string (unsigned val);
string to_string (unsigned long val);
string to_string (unsigned long long val);
string to_string (float val);
string to_string (double val);
string to_string (long double val);
功能：
将数值转化为字符串。返回对应的字符串。
一个实现的例子：
#include <iostream>   
#include <string>     
using namespace std;
int main()
{
    string pi = "pi is " + std::to_string(3.1415926);
    string perfect = to_string(1 + 2 + 4 + 7 + 14) + " is a perfect number";
    cout << pi << '\n';
    cout << perfect << '\n';
    system("pause");
    return 0;
}

五、一些语法知识

1、深拷贝浅拷贝：通过在堆区开辟一段数据格式和p.m_height一样的内存存放

m_height = new int(*p.m_height);

2、静态成员就是在成员变量和成员函数前加上关键字static，称为静态成员
静态成员分为：

静态成员变量：
	所有对象共享同一份数据
	在编译阶段分配内存
	类内声明，类外初始化
静态成员函数：
	所有对象共享同一个函数
	静态成员函数只能访问静态成员变量

查找算法、数组、队列–>二叉树

1、

		for (int price: prices) {
            maxprofit = max(maxprofit, price - minprice);
            minprice = min(price, minprice);
        }

for循环条件语句中的这个（int num:nums）是什么意思？java中的for each函数的意思

再比如:

#include<iostream>
#include<vector>
using namespace std;
int main() {
int a[] = { 1,2,3,5,2,0 };
vector<int>counts(a,a+6);
for (auto count : counts)
	cout<< count<< " ";
cout << endl;
return 0;

输出  1 2 3 5 2 0 

2、数组 num也可以用num.size()来指知道组长度。或者nums.length，有时候不支持

二维数组的行列长度获取：

sizeof(array[0][0])：一个元素占用的空间，
sizeof(array[0])：一行元素占用的空间，
sizeof(array)：整个数组占用的空间，

行数 = sizeof(array)/sizeof(array[0]);
列数 = sizeof(array[0])/sizeof(array[0][0])；

行数=matrix.size()
列数= matrix[0].size()

3、二分法、DP、DFS、层序遍历BFS
4、对于有序的二维数组可以用二叉树的思想去遍历，寻找目标值！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！怎么想到的反向遍历

裂开：注意编译器的用例vector数组可能出现 [[ ]]，在求行列数的时候要具体以带进循环，不能再循环外计算好再在条件中判断

5、
二分法的时间复杂度是O(logn),所以在算法中，比O(n)更优的时间复杂度几乎只能是O(logn)的二分法。

根据时间复杂渡来倒推算法也是面试中的常用策略：题目中若要求算法的时间复杂度是O(logn)，那么这个算法基本上就是二分法。

二分法可以解决旋转数组问题不论是有重复值还是没有重复值,有重复值就要注意mid区间值相等时,这时不能得出寻找值到底在mid的前面还是后面,比如[7 0 1 1 1 1] , [7 1 1 0 1] 实际上，当出现 m=r 时，一定有区间 l=m || m=r所有元素相等或两者皆满足,对于寻找此类数组的最小值问题，可直接放弃二分查找，而使用线性查找替代。暴力慢慢缩小相等值的范围

6 、搜索与回溯算法
递归与回溯的区别

递归是一种算法结构。递归会出现在子程序中，形式上表现为直接或间接的自己调用自己。典型的例子是阶乘，
计算规律为：n!=n×(n−1)!
回溯是一种算法思想，它是用递归实现的。回溯的过程类似于穷举法，但回溯有“剪枝”功能，即自我判断过程。例如有求和问题，给定有 7 个元素的组合 [1, 2, 3, 4, 5, 6, 7]，求加和为 7 的子集。累加计算中，选择 1+2+3+4 时，判断得到结果为 10 大于 7，那么后面的 5, 6, 7 就没有必要计算了。这种方法属于搜索过程中的优化，即“剪枝”功能。
用一个比较通俗的说法来解释递归和回溯：
我们在路上走着，前面是一个多岔路口，因为我们并不知道应该走哪条路，所以我们需要尝试。尝试的过程就是一个函数。
我们选择了一个方向，后来发现又有一个多岔路口，这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上，再做一次尝试，即在函数内部再调用一次函数，这就是递归的过程。
这样重复了若干次之后，发现这次选择的这条路走不通，这时候我们知道我们上一个路口选错了，所以我们要回到上一个路口重新选择其他路，这就是回溯的思想。

① 二叉树层序遍历DFS：二叉树在很大程度上解决了这个缺点，二叉树是按值来保存元素，也按值来访问元素。怎么做到呢，和链表一样，二叉树也是由一个个节点组成，不同的是链表用指针将一个个节点串接起来，形成一个链，如果将这个链“拉直”，就像平面中的一条线，是一维的。而二叉树由根节点开始发散，指针分别指向左右两个子节点，像树一样在平面上扩散，是二维的。
②遍历二叉树时发现：有个很神奇的点：不管是队列还是二维数组，xx.size()能获得同行的长度！！！！而且，要注意输出是啥，是直接一维数组，还是数组里面以每层为数组组成的二维数组！！！注意将左子序和右子序装入队列时，size的值不能更新，得在装入的循环往外面计算原来的行长度
③ deque双端操作的队列

push_back(elem); //在容器尾部添加一个数据
push_front(elem); //在容器头部插入一个数据
pop_back(); //删除容器最后一个数据
pop_front(); //删除容器第一个数据
insert(pos,elem); //在pos位置插入一个elem元素的拷贝，**返回新数据的位置**。
at(int idx); //返回索引idx所指的数据
operator[]; //返回索引idx所指的数据
front(); //返回容器中第一个数据元素
back(); //返回容器中最后一个数据元素

④ 对称性递归
递归：函数体+返回值，函数体里面可以自己构造成员函数，在返回值里面可以调用函数体的成员函数，其实就是写一个迭代，给定下一次函数体的初值，而函数体中写着啥时候结束迭代，一般比如判断二叉树的根节点是否为空，就是说是不是遍历完了；如判断平衡二叉树时调用二叉树高度函数。完全嵌套！！！
能作为递归的一些判断条件：双树单树
一些例子：对称性递归的例子

相同的树：

bool isSameTree(TreeNode*p, TreeNode*q)
{
    if (!p && !q)
        return true;
    return p && q && p->val == q->val && (isSameTree(p->left, q->left)) && (isSameTree(p->right, q->right));
}

二叉树的最大深度：

int height(TreeNode*root)
{
    if (!root)
        return 0;
    else
        return max(height(root->left), height(root->right)) + 1;
}

平衡二叉树；

bool isBalanced(TreeNode*&root)
{
    if (!root)
        return true;
    return (abs(height(root->left) - height(root->right)) <= 1) && isBalanced(root->left) && isBalanced(root->right);
}

单值二叉树：

bool isUnivalTree(TreeNode*root)
{
    if (!root) 
        return true;
    if ((root->left && root->left->val != root->val) || (root->right && root->right->val != root->val))
        return false; 
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

另一个的子树：

bool isSubtree(TreeNode*root1, TreeNode*root2)
{
    if (!root1 || !root2)
        return false;
    if (isSameTree(root1, root2))
        return true;
    return isSubtree(root1->left, root2) || isSubtree(root1->right, root2);
}

翻转二叉树：

TreeNode*invertTree(TreeNode*root)
{
    if (!root)
        return nullptr;
    TreeNode*left = invertTree(root->left);
    TreeNode*right = invertTree(root->right);
    root->left = right;
    root->right = left;
    return root;
}
注：上面是官方的不容易理解，写了自己的版本（但还是试着理解了一下，就是
说新创建了两个root的左右节点，对他进行赋值操作，注意是赋值不是return，赋
值完成之后程序虽然调用了invert，但是不会直接return到下一次循环，就继续往
下执行，在下面的时候才交换了指针的指向，而我常规思路是，指针反转就可）： 

TreeNode* invertTree(TreeNode* root) {
    if (root == nullptr) {
        return nullptr;
    }
    TreeNode *temp = root->left;
    root->left = root->right;
    root->right = temp;
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

合并二叉树：

TreeNode*mergeTrees(TreeNode*root1, TreeNode*root2)
{
    if (!root1)
        return root2;
    if (!root2)
        return root1;
    if (root1 && root2)
        root1->val += root2->val;
    root1->left = mergeTrees(root1->left, root2->left);    //递归合并左子树
    root1->right = mergeTrees(root1->right, root2->right); //递归合并右子树
    return root1;
}

判断一棵树是不是对称树）：

bool isSymmetric(TreeNode*root)
{
    return isMirror(root, root);
}

bool isMirror(TreeNode*p, TreeNode*q)
{
    if (!p && !q)
        return true;
    if (!p || !q)
        return false;
    return (p->val == q->val) && (isMirror(p->left, q->right)) && (isMirror(p->right, q->left));
}

注意判断条件：有可能该树缺叶，所以构造镜像树后，左跟右、右跟左叶节点都得比较

判断一棵树是不是另一棵树的子结构；

// hasSubStructure函数是判断如果A,B根节点相同，B是不是A的子结构
bool hasSubStructure(TreeNode*A, TreeNode*B)
{
    if (!B)        //递归结束条件1：A的一个节点B的对应位置没有,可以认为是子结构
        return true;
    if (!A || A->val != B->val)  //递归结束条件2：B的一个节点A的对应位置没有 / A,B对应位置节点值不同，此时必然不可能是子结构
        return false;
    return hasSubStructure(A->left, B->left) && hasSubStructure(A->right, B->right); //返回值：继续在对应位置递归判断
}


bool isSubStructure1(TreeNode<T> *A, TreeNode<T> *B)
{
    if (!A || !B)   //特殊判断
        return false;
    // 根节点相同的话直接进入比较，根节点不相同看B是不是A的左/右子树的子结构
    return hasSubStructure(A, B) || isSubStructure1(A->left, B) || isSubStructure1(A->right, B);
}

注：子结构和子树不一样的点在于子结构不能只利用根节点进行对称性递归，需要构造辅助函数去判断当两棵树根节点值相同时一棵树是否为另一棵树子结构

动态规划问题

1、斐波拉切数列：原来递归才是传统解法啊！！！递归深度过大，就会导致栈溢出。
2、青蛙跳台阶：一样的，迭代无敌
我一直会的原来是动态规划的解法！！！将每次前两数之和存起来，便于下次直接使用，这样子，我们就把一个栈溢出的问题，变为了单纯的数学加法，大大减少了内存的压力。
我的解法：

class Solution {
public:
    int fib(int n) {
        if(n==0){
            return 0;
        }
        if(n==1||n==2){
            return 1;
        }
        int Fn_2=1;
        int Fn_1=1;
        int i,Fn;
        for(i=3;i<=n;i++){
            Fn=(Fn_1+Fn_2)%1000000007;
            Fn_2=Fn_1;
            Fn_1=Fn;
        }
        return Fn;
    }
};

递归：

总结：做这道题感触，迭代的方法更加简单，递归方法如果没有哈希表unordered_map肯定会超过时间，迭代和递归的区别：递归是从n一直到基础条件，而迭代则是从基础条件出发推导到n，可以说递归是逆向过程，而迭代是正向过程，所以我觉得可以用迭代的方法，往往也可以用递归；动态规划基本都用是迭代的方法，当然是用递归也是可以，个人觉得迭代熟悉。

3、买股票最佳时机：
有这么几点吧：①在我们设计算法的时候算法内容不涉及到修改数据本身，而只是去遍历，与其去操作指针，不如直接用for(auto num:nums)遍历 ②容易陷入一个误区：买卖完第一次才能进行后面的，所以误用暴力遍历（操作数3以上没法人脑计算），更不用说多次买卖求最优了；所以买股票的精髓在于如何去更新每次的花费状态，最大程度降低复杂度O（n）可以为啥不用，真的是 !!!
买股票

3、二维数组中的做大路径和/最小路径和
Vector<类型>标识符(最大容量,初始所有值)

以及vector< vector > dp(m, vector(n) )

常见定义方法：
(1) vector a(5); //定义了5个整型元素的向量（<>中为元素类型名，它可以是任何合法的数据类 型），但没有给出初值，其值是不确定的。
（2）vector a(5,1); //定义了5个整型元素的向量,且给出每个元素的初值为1
（3）vector a(b); //用b向量来创建a向量，整体复制性赋值
（4）vector a(b.begin(),b.begin+3); //定义了a值为b中第0个到第2个（共3个）元素
（5）int b[7]={1,2,3,4,5,9,8};
vector a(b,b+7); //从数组中获得初值

重点：vector< vector > v(m, vector(n) );定义了一个vector容器，元素类型为vector，初始化为包含m个vector对象，每个对象都是一个新创立的vector对象的拷贝，而这个新创立的vector对象被初始化为包含n个0。
4、滚动数组优化动态规划

① 先判断出状态转移方程，是怎么样的，也就是从头到尾分析满足啥关系，用vector数组去存储对应的值时，需要存储的数据较多，空间不够优化，所以可以用滚动数组，只记录用到的值，然后迭代。

② 进一步优化空间：迭代的时候++i，省去了存储临时变量，for循环中++i 和 i++ 的区别
根据上面的for循环的语法定义 ++i 和 i++的结果是一样的，都要等代码块执行完毕才能执行语句3，但是性能是不同的。在大量数据的时候++i的性能要比i++的性能好原因：
i++由于是在使用当前值之后再+1，所以需要一个临时的变量来转存。
而++i则是在直接+1，省去了对内存的操作的环节，相对而言能够提高性能
③在leetcode刷题时候，看见有答案使用 vector map(128,0) 代替 unordered_map<char,int> map的功能， 这种做法我应该学习吗？还有这样写的 vector map(128) 更离谱。很正常的操作啊，空间换时间，map变查表。不过128的确稍有问题，我的话还是会开256的大小（反正用不上的不会拖累速度，这么小都在L1里）
④链表代码中常见用法区别：一般此代码用在没有头结点或者需要双指针遍历等情况

1.  初始化一个空节点，没有赋值，指针指向为list（不推荐）
ListNode list = new ListNode();
2.  初始化一个空节点，初始赋值为0，指针指向为list
ListNode list = new ListNode(0);
3.  初始化一个空节点，初始赋值为0，并且list的下一个next指针指向head，指针指向为list
ListNode list = new ListNode(0,head);
4.  定义一个空链表
ListNode list=null;

5、排序算法
快速排序
6、双指针，对于排序数组好用
vector 数组 类型的返回: 返回空 return { }; 返回几个元素 return { nums [ i ] ,nums[ j ] };

字符串拼接，直接用 ‘’ ‘’ + ‘’ ‘’ 真神奇，或者 s.append ( char ss) 追加字符

初始化赋值的时候，比如使用 int left,right=s.size();可能会报错 int left=0,right=s.size();则不会！

substr(pos , n)的用法；

对于 while 或者 for 的判断条件，大于0，小于0直接写确切的就可 判断int a 为非负 ; if (a)不等于