END-TO-END OPTIMIZED IMAGE COMPRESSION论文阅读

END-TO-END OPTIMIZED IMAGE COMPRESSION

单词

image compression 图像压缩

quantizer 量化器

rate–distortion performance率失真性能

a variant of 什么什么的一个变体

construct 构造

entropy 熵

discrete value 离散值

摘要：

We describe an image compression method, consisting of a nonlinear analysis transformation, a uniform quantizer, and a nonlinear synthesis transformation. The transforms are constructed in three successive stages of convolutional linear filters and nonlinear activation functions. Unlike most convolutional neural networks, the joint nonlinearity is chosen to implement a form of local gain control, inspired by those used to model biological neurons. Using a variant of stochastic gradient descent, we jointly optimize the entire model for rate–distortion performance over a database of training images, introducing a continuous proxy for the discontinuous loss function arising from the quantizer. Under certain conditions, the relaxed loss function may be interpreted as the log likelihood of a generative model, as implemented by a variational autoencoder. Unlike these models, however, the compression model must operate at any given point along the rate– distortion curve, as specified by a trade-off parameter. Across an independent set of test images, we find that the optimized method generally exhibits better rate–distortion performance than the standard JPEG and JPEG 2000 compression methods. More importantly, we observe a dramatic improvement in visual quality for all images at all bit rates, which is supported by objective quality estimates using MS-SSIM.

我们描述了一种图像压缩方法，包括非线性分析变换、均匀量化器和非线性合成变换。这些变换是在卷积线性滤波器和非线性激活函数的三个连续阶段中构造的。与大多数卷积神经网络不同，受用于模拟生物神经元的网络的启发，选择联合非线性来实现一种局部增益控制形式。使用随机梯度下降的变体，我们在训练图像数据库上联合优化整个模型的率失真性能，引入量化器产生的不连续损失函数的连续代理。在某些条件下，松弛损失函数可以解释为由变分自动编码器实现的生成模型的对数似然。然而，与这些模型不同的是，压缩模型必须在速率失真曲线上的任何给定点上运行，如权衡参数所指定。在一组独立的测试图像中，我们发现优化方法通常比标准 JPEG 和 JPEG 2000 压缩方法表现出更好的率失真性能。更重要的是，我们观察到所有比特率下所有图像的视觉质量都有显着改善，这得到了使用 MS-SSIM 的客观质量估计的支持

1.INTRODUCTION

Data compression is a fundamental and well-studied problem in engineering, and is commonly formulated with the goal of designing codes for a given discrete data ensemble with minimal entropy (Shannon, 1948).The solution relies heavily on knowledge of the probabilistic structure of the data, and thus the problem is closely related to probabilistic source modeling. However, since all practical codes must have finite entropy, continuous-valued data (such as vectors of image pixel in- tensities) must be quantized to a finite set of discrete values, which introduces error. In this context, known as the lossy compression problem, one must trade off two competing costs: the entropy of the discretized representation (rate) and the error arising from the quantization (distortion).Different compression applications, such as data storage or transmission over limited-capacity channels, demand different rate–distortion trade-offs.

数据压缩是工程中一个基本且经过充分研究的问题，通常以为给定离散数据集合设计具有最小熵的代码为目标而制定（Shannon，1948）。该解决方案在很大程度上依赖于数据概率结构的知识，因此该问题与概率源建模密切相关。**然而，由于所有实际代码都必须具有有限的熵，因此连续值数据（例如图像像素强度的向量）必须量化为一组有限的离散值，这会引入误差。**在这种情况下，称为有损压缩问题，必须权衡两个相互竞争的成本：离散表示的熵（速率）和量化产生的误差（失真）。不同的压缩应用，例如数据存储或通过有限容量通道传输，需要不同的速率-失真权衡

Joint optimization of rate and distortion is difficult.Without further constraints, the general problem of optimal quantization in high-dimensional spaces is intractable (Gersho and Gray, 1992).For this reason, most existing image compression methods operate by linearly transforming the data vector into a suitable continuous-valued representation, quantizing its elements independently, and then encoding the resulting discrete representation using a lossless entropy code (Wintz, 1972; Netravali and Limb,1980).

速率和失真的联合优化很困难。如果没有进一步的约束，高维空间中最优量化的一般问题是棘手的（Gersho 和 Gray，1992）。因此，大多数现有的图像压缩方法通过将数据向量线性变换为合适的连续值表示，独立量化其元素，然后使用无损熵代码对所得离散表示进行编码（Wintz，1972；Netravali 和 Limb， 1980）。

This scheme is called transform coding due to the central role of the transformation.For example, JPEG uses a discrete cosine transform on blocks of pixels, and JPEG 2000 uses a multi-scale orthogonal wavelet decomposition. Typically, the three components of transform coding methods – transform, quantizer, and entropy code – are separately optimized (often through manual parameter adjustment).

由于变换的核心作用，该方案被称为变换编码。例如，JPEG 对像素块使用离散余弦变换，而 JPEG 2000 使用多尺度正交小波分解。通常，变换编码方法的三个组成部分——变换、量化器和熵代码——是分别优化的（通常通过手动参数调整）。

We have developed a framework for end-to-end optimization of an image compression model based on nonlinear transforms (figure 1).Previously, we demonstrated that a model consisting of linear– nonlinear block transformations, optimized for a measure of perceptual distortion, exhibited visually superior performance compared to a model optimized for mean squared error (MSE) (Ball ́e, La- parra, and Simoncelli,2016).Here, we optimize for MSE, but use a more flexible transforms built from cascades of linear convolutions and nonlinearities.Specifically, we use a generalized divisive normalization (GDN) joint nonlinearity that is inspired by models of neurons in biological visual systems, and has proven effective in Gaussianizing image densities (Ball ́e, Laparra, and Simoncelli, 2015).This cascaded transformation is followed by uniform scalar quantization (i.e., each element is rounded to the nearest integer), which effectively implements a parametric form of vector quantization on the original image space.The compressed image is reconstructed from these quantized values using an approximate parametric nonlinear inverse transform.

我们开发了一个基于非线性变换的图像压缩模型端到端优化框架（图 1）。之前，我们证明了由线性-非线性块变换组成的模型，针对感知失真的测量进行了优化，与针对均方误差（MSE）优化的模型（Ball ́e、Laparra 和 Simoncelli， 2016）。在这里，我们针对 MSE 进行优化，但使用由线性卷积和非线性级联构建的更灵活的变换。具体来说，我们使用广义除法归一化（GDN）联合非线性，其灵感来自生物视觉系统中的神经元模型，并已被证明在高斯化图像密度方面有效（Ball ́e、Laparra 和 Simoncelli，2015）。这种级联变换之后是均匀标量量化（即，每个元素都舍入到最接近的整数），这有效地在原始图像空间上实现了矢量量化的参数形式。使用近似参数非线性逆变换从这些量化值重建压缩图像。

For any desired point along the rate–distortion curve, the parameters of both analysis and synthesis transforms are jointly optimized using stochastic gradient descent.To achieve this in the presence of quantization (which produces zero gradients almost everywhere), we use a proxy loss function based on a continuous relaxation of the probability model, replacing the quantization step with additive uniform noise.The relaxed rate–distortion optimization problem bears some resemblance to those used to fit generative image models, and in particular variational autoencoders (Kingma and Welling, 2014; Rezende, Mohamed, and Wierstra, 2014), but differs in the constraints we impose to ensurethat it approximates the discrete problem all along the rate–distortion curve.Finally, rather than reporting differential or discrete entropy estimates, we implement an entropy code and report performance using actual bit rates, thus demonstrating the feasibility of our solution as a complete lossy compression method.

对于速率失真曲线上的任何所需点，使用随机梯度下降联合优化分析和综合变换的参数。为了在存在量化（几乎在任何地方产生零梯度）的情况下实现这一目标，我们使用基于概率模型的连续松弛的代理损失函数，用加性均匀噪声代替量化步骤。松弛率失真优化问题与用于拟合生成图像模型的问题有一些相似之处，特别是变分自动编码器（Kingma 和 Welling，2014 年；Rezende、Mohamed 和 Wierstra，2014 年），但不同之处在于我们为确保它近似于沿着率失真曲线的离散问题。最后，我们不是报告差分或离散熵估计，而是使用实际比特率实现熵代码并报告性能，从而证明了我们的解决方案作为完整有损压缩方法的可行性。

2.CHOICE OF FORWARD, INVERSE, AND PERCEPTUAL TRANSFORMS

正向、反向和感知变换的选择

Most compression methods are based on orthogonal linear transforms, chosen to reduce correlations in the data, and thus to simplify entropy coding.But the joint statistics of linear filter responses exhibit strong higher order dependencies.These may be significantly reduced through the use of joint localnonlinear gain control operations (Schwartz and Simoncelli, 2001; Lyu, 2010; Sinz and Bethge, 2013), inspired by models of visual neurons (Heeger, 1992; Carandini and Heeger, 2012).Cascaded versions of such models have been used to capturemultiple stages of visual transformation (Simoncelli and Heeger, 1998; Mante, Bonin, and Carandini, 2008).Some earlier results suggest that incorporating local normalization in linear block transform coding methods can improve coding performance (Malo et al., 2006), and can improve object recognition performance of cascaded convolutional neural networks (Jarrett et al., 2009).However, the normalization parameters in these cases were not optimized for the task.Here, we make use of a generalized divisive normalization (GDN) transformwith optimized parameters, that we have previously shown to be highly efficient in Gaussianizing the local joint statistics of natural images, much more so than cascades of linear transforms followed by pointwise nonlinearities (Ball ́e, Laparra, and Simoncelli, 2015)

大多数压缩方法都基于正交线性变换，选择这些方法是为了减少数据中的相关性，从而简化熵编码。但是线性滤波器响应的联合统计表现出强烈的高阶依赖性。通过使用联合局部可以显着减少这些依赖性。非线性增益控制操作（Schwartz 和 Simoncelli，2001；Lyu，2010；Sinz 和 Bethge，2013），受到视觉神经元模型的启发（Heeger，1992；Carandini 和 Heeger，2012）。此类模型的级联版本已用于捕获视觉变换的多个阶段（Simoncelli 和 Heeger，1998；Mante、Bonin 和 Carandini，2008）。一些早期结果表明，在线性块变换编码方法中结合局部归一化可以提高编码性能（Malo 等，2006） ，并且可以提高级联卷积神经网络的对象识别性能（Jarrett et al., 2009）。但是，这些情况下的归一化参数并未针对该任务进行优化。在这里，我们利用广义除法归一化（GDN）变换使用优化的参数，我们之前已经证明它在对自然图像的局部联合统计进行高斯化方面非常有效，比线性变换级联和逐点非线性要高效得多（Ball ́e、Laparra 和 Simoncelli，2015）

Note that some training algorithms for deep convolutional networks incorporate “batch normalization”, rescaling the responses of linear filters in the network so as to keep it in a reasonable operating range (Ioffe and Szegedy, 2015).This type of normalization is different from local gain control in that the rescaling factor is identical across all spatial locations.Moreover, once the training is completed, the scaling parameters are typically fixed, which turns the normalization into an affine transformation with respect to the data – unlike GDN, which is spatially adaptive and can be highly nonlinear.

请注意，深度卷积网络的一些训练算法包含“批量归一化”，重新调整网络中线性滤波器的响应，以使其保持在合理的操作范围内（Ioffe 和 Szegedy，2015）。这种类型的归一化与局部增益控制不同，因为重新缩放因子在所有空间位置上都是相同的。此外，一旦训练完成，缩放参数通常是固定的，这会将归一化转变为针对数据的仿射变换——与空间自适应且高度非线性的 GDN 不同。

Specifically, our analysis transform ga consists of three stages of convolution, subsampling, and divisive normalization.We represent the ith input channel of the kth stage at spatial location (m, n) as u(k) i (m, n).The input image vector x corresponds to u(0) i (m, n), and the output vector y is u(3) i (m, n).Each stage then begins with an affine convolution:

具体来说，我们的分析变换 $g_a$ 由卷积、子采样和除法归一化三个阶段组成。我们将空间位置 (m, n) 处第 k 级的第 i 个输入通道表示为$ u^{(k)} i (m, n)$。输入图像向量x对应于$u^{(0)} i (m, n)$，输出向量y为$u^{(3)}_ i (m, n)$。然后每个阶段都从仿射卷积开始：

(1)

where ∗ denotes 2D convolution. This is followed by downsampling:

其中*表示2D卷积。接下来是下采样：

(2)

where sk is the downsampling factor for stage k.Each stage concludes with a GDN operation

其中 $s_k$ 是阶段 k 的下采样因子。每个阶段都以 GDN 操作结束

(3)

The full set of h, c, β, and γ parameters (across all three stages) constitute the parameter vector φ to be optimized

全套 h、c、β 和 γ 参数（跨所有三个阶段）构成要优化的参数向量 φ

Analogously, the synthesis transform gs consists of three stages, with the order of operations re- versed within each stage, downsampling replaced by upsampling, and GDN replaced by an approx- imate inverse we call IGDN (more details in the appendix).We define ˆu(k) i (m, n) as the input to the kth synthesis stage, such that ˆy corresponds to ˆu(0) i (m, n), and ˆx to ˆu(3) i (m, n).Each stage then consists of the IGDN operation:

类似地，合成变换 $g_s $由三个阶段组成，每个阶段内的操作顺序颠倒，下采样被上采样取代，GDN被我们称为IGDN的近似逆代替（更多详细信息参见附录）。我们将$ \hat{u}^{(k)}_ i (m, n) $定义为第 k 个合成阶段的输入，使得 $\hat y $对应于 ${\hat{u}}_i^{(0)}(m,n)$，而 $\hat{x}$ 对应于$ \hat u^{(3)}_ i (m, n)$ 。每个阶段都包含 IGDN 操作：

(4)

which is followed by upsampling

接下来是上采样

(5)

where ˆsk is the upsampling factor for stage k.Finally, this is followed by an affine convolution:

其中 $\hat s_k $是阶段 k 的上采样因子。最后，进行仿射卷积：

(6)

Analogously, the set of ˆh, ˆc, ˆβ, and ˆγ make up the parameter vector θ.Note that the down- /upsampling operations can be implemented jointly with their adjacent convolution, improving com- putational efficiency.

类似地，$\hat{h}$、$\hat{c}$、$\hat{\beta }$ 和$ \hat γ$ 的集合构成了参数向量 θ。请注意，下采样/上采样操作可以与其相邻卷积联合实现，从而提高计算效率。

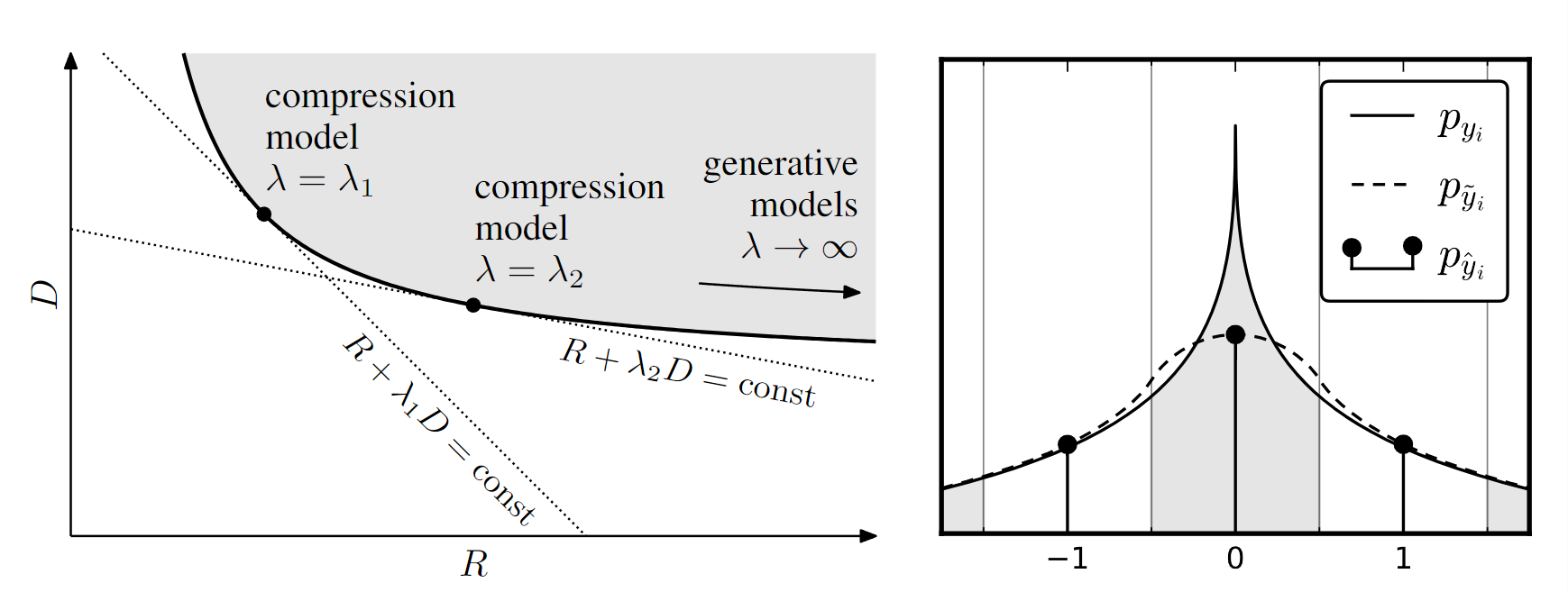
Figure 2:Left: The rate–distortion trade-off.The gray region represents the set of all rate–distortion values that can be achieved (over all possible parameter settings).Optimal performance for a given choice of λ corresponds to a point on the convex hullof this set with slope −1/λ.Right: One- dimensional illustration of relationship between densities of yi (elements of code space), ˆyi (quan- tized elements), and ̃yi (elements perturbed by uniform noise).Each discrete probabilityin pˆyi equals the probability mass of the density pyi within the corresponding quantization bin (indicated by shading).The density p ̃yi provides a continuous function that interpolates the discrete probability values pˆyi at integer positions

左：率失真权衡。灰色区域表示可以实现的所有率失真值的集合（在所有可能的参数设置上）。给定 λ 选择的最佳性能对应于凸包上的点该集合的斜率为−1/λ。右图：$y_i$（代码空间元素）、${\hat{y}}_i$（量化元素）和 ${\tilde{y}}_i$（受均匀噪声扰动的元素）密度之间关系的一维图示。每个离散概率$ p_{\hat yi} $等于相应量化仓内密度 $p_{yi} $的概率质量（由阴影表示）。密度\tilde{p}yi提供了一个连续函数，可在整数位置插值离散概率值$ p_{ \hat y_i}$

In previous work, we used a perceptual transform gp, separately optimized to mimic human judgements of grayscale image distortions (Laparra et al., 2016), and showed that a set of one-stage transforms optimized for this distortion measure ledto visually improved results (Ball ́e, Laparra, and Simoncelli, 2016).Here, we set the perceptual transform gp to the identity, and use mean squared error (MSE) as the metric (i.e., d(z, ˆz) = ‖z − ˆz‖2 2).This allows a more interpretable comparison to existing methods, which are generally optimized for MSE, and also allows optimization for color images, for which we do not currently have a reliable perceptual metric.

在之前的工作中，我们使用了感知变换$ g_pKaTeX parse error: Expected 'EOF', got '́' at position 75: …致视觉效果得到改善（Ball ̲́e、Lapar