[2002J4]过河卒

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0,0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

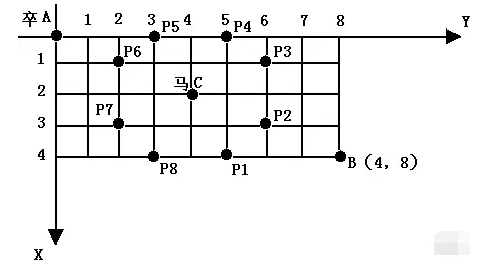
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 100% 的数据，1≤n,m≤20，0≤ 马的坐标 ≤20。

#include <iostream>
#include <algorithm>
using namespace std;

long long f[30][30];
int dis[8][2]={{1,2},{-1,2},{1,-2},{-1,-2},{2,1},{-2,1},{2,-1},{-2,-1}};
int main()
{
	//输入
	int n,m,mx,my;
	cin>>n>>m>>mx>>my;
	//初始化边界
	f[0][0]=1;
	//初始化“马”
	f[mx][my]=-1;
	for(int i=0;i<8;i++)
	{
		int x=mx+dis[i][0],y=my+dis[i][1];
		if(x>=0&&x<=n&&y>=0&&y<=m)
			f[x][y]=-1;
	}
	//遍历赋值
	for(int i=0;i<=n;i++)
		for(int j=0;j<=m;j++)
			if(f[i][j]!=-1&&!(i==0&&j==0))
			{
				long long q=(i>0 ? max(0ll,f[i-1][j]) : 0);
				long long w=(j>0 ? max(0ll,f[i][j-1]) : 0);
				f[i][j]=q+w;
			}
	//输出
	if(f[n][m]==-1)
		cout<<0;
	else
		cout<<f[n][m];
	return 0;
}

这道题是DP，小坑特别多，交了8遍才过！主要问题有：base，优先级，long long，等等，等等……主要难点在“遍历赋值”区。