计数排序 + 基数排序

计数排序

统计给定一个集合中，每个数字出现的次数，然后根据次数，依次将对应数组按顺序放回
但是计数排序有局限性，只能一次统计已知一定范围内的元素。

如下列示例代码中，找到数组元素最大值，然后创建以最大值为大小的数组，作为桶进行技术，会造成空间浪费，也有一定局限性。

代码实现

	// only for 0~200 value
	public static void countSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int max = Integer.MIN_VALUE;
		for (int i = 0; i < arr.length; i++) {
			max = Math.max(max, arr[i]);
		}
		int[] bucket = new int[max + 1];
		for (int i = 0; i < arr.length; i++) {
			bucket[arr[i]]++;
		}
		int i = 0;
		for (int j = 0; j < bucket.length; j++) {
			while (bucket[j]-- > 0) {
				arr[i++] = j;
			}
		}
	}

基数排序

通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}

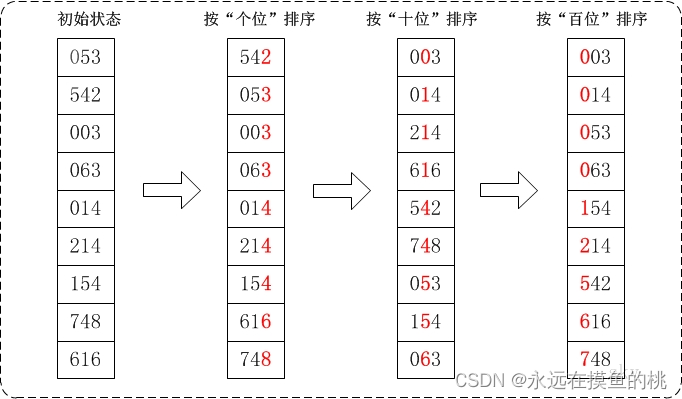
大概流程就是从个位开始，入桶进行排序；然后找更高位接着，入桶进行排序，依次类推，最终使得数组有序。
局限性：受限于元素种类，一般来讲元素要是10进制的正整数

代码实现

public class RadixSort {
    public static void main(String[] args) {
        int[] arr = new int[] {53, 3, 542, 748, 14, 214, 154, 63, 616};
        radixSort(arr);
        for (int i = 0; i < arr.length; i++) {
            System.out.println(arr[i]);
        }
    }

    public static void radixSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        radixSort(arr, 0, arr.length - 1, maxbits(arr));
    }

    // 找最大值的十进制位数digit
    private static int maxbits(int[] arr) {
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            max = Math.max(max, arr[i]);
        }

        int res = 0;
        while (max != 0) {
            res++;
            max /= 10;
        }
        return res;
    }

    // arr[L..R]排序  ,  最大值的十进制位数digit
    public static void radixSort(int[] arr, int L, int R, int digit) {
        int radix = 10; // 桶个数
        int i = 0;
        int j = 0;
        // 有多少个数就准备多大的辅助空间
        int[] help = new int[R - L + 1];
        for (int d = 1; d <= digit; d++) {  // 有多少位就进出几次
            // 10个空间
            // count[0] 当前位(d位)是0的数字有多少个
            // count[1] 当前位(d位)是(0和1)的数字有多少个
            // count[2] 当前位(d位)是(0、1和2)的数字有多少个
            // count[i] 当前位(d位)是(0~i)的数字有多少个
            // 相当于10和桶
            int[] count = new int[radix]; // count[0..9]
            for (i = L; i <= R; i++) {
                // 获取d位上的数，在count桶中对应位置+1
                j = getDigit(arr[i], d);
                count[j]++;
            }

            // 求前缀和，遍历所有桶，进行前缀累加
            for (i = 1; i < radix; i++) {
                count[i]  = count[i - 1] + count[i];
            }
            // 根据前缀和，将对应的数字放到辅助数组的正确位置上
            for (i = R; i >= L; i--) {
                j = getDigit(arr[i], d);
                // 设count[j]代表位置值为c；则存储的下标范围为 0~c-1，从后往前存储
                help[count[j] - 1] = arr[i];
                // 存入一个值，则count[j]--
                count[j]--;
            }
            // 最终将这次排序的结果复制到原数组中，进行下一位数的排序
            for (i = L, j = 0; i <= R; i++, j++) {
                arr[i] = help[j];
            }
        }
    }

    // 获取x的第d位数字
    public static int getDigit(int x, int d) {
        return ((x / ((int) Math.pow(10, d - 1))) % 10);
    }
}