【C++】二叉树

二叉树的概念

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。二叉树可以为空树，通常子树被称为”左子树“和”右子树“
比如下图就是一棵二叉树

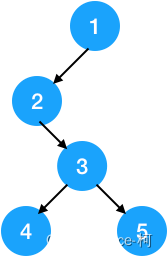
二叉树的每个节点最多有两棵子树（不存在度大于2的节点），二叉树的子树有左右之分，次序不能颠倒
二叉树的第i层，最多有$2^{i-1}$个结点
深度为k的二叉树，最多有$2^k-1$个结点
对于任何一颗二叉树，如果其叶结点数为$n0$，度为2的节点数为$n2$，则$n0=n2+1$
对于最后一个结论可以这么理解，当我们给某个节点新增一个子节点时，如果原节点度数为0则原节点为叶节点，添加后原节点度数为1，新节点为叶节点，所以$n0$和$n2$都不变
如果原节点度数为1，添加后原节点度数为2，$n2$会增加1，新增的节点为叶节点，所以$n0$也会增加1，该等式仍然成立

特殊的二叉树

满二叉树

一棵深度为k，且有$2^k-1$个结点的二叉树，成为满二叉树。满二叉树每一层的结点都是满的
如下图

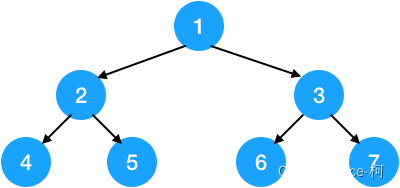
完全二叉树

在一棵二叉树中，除了最后一层外，其余层都是满的，或者是在右边缺少连续若干结点，则此二叉树为完全二叉树。具有n个结点的完全二叉树的深度是log(n+1)log(n+1)