A level数学真题解析及运用

最新推荐文章于 2022-11-18 11:54:39 发布

原创

最新推荐文章于 2022-11-18 11:54:39 发布 · 2.5k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#学习

本文介绍了A level数学中的复数章节，特别是阿干特图的概念，及其与笛卡尔坐标系的区别。阿干特图用于表示复数，包括三种表现形式：模-幅角形式、极坐标形式和指数形式。文章通过真题示例展示了如何在考试中运用这些概念，帮助考生理解和应对相关题目。

在A level考试9709数学科目中pure mathematics 3考卷考察范围内有一章节名为complex number，即复数章节。这部分知识点虽然理解难度不大，但是在我国普通高中的数学学习中涉及的较少，考生在接受上有比较大的难度，解题运用方面也会多少受阻。尤其其中的the Argand diagram（阿干特图）对很多同学来说无疑是一只拦路虎。

现行版本CAIE考试局pure mathematics 2&3的教材中，第十一章也就是最后一张，是复数内容，其中包含5节内容，前两节简述了虚数i和复数的概念，第三节出现了虚数的坐标体系，也就是the Argand diagram（阿干特图）。

1.什么是The Argand Diagram（阿干特图）

那the Argand diagram（阿干特图）到底是什么呢？阿干特图类似于笛卡尔坐标系，由两个互相垂直的轴组成，其区别在于阿干特图的一轴为实数轴，另一为虚数轴，而笛卡尔坐标系两轴均为实数轴。下图显示二者的区别：

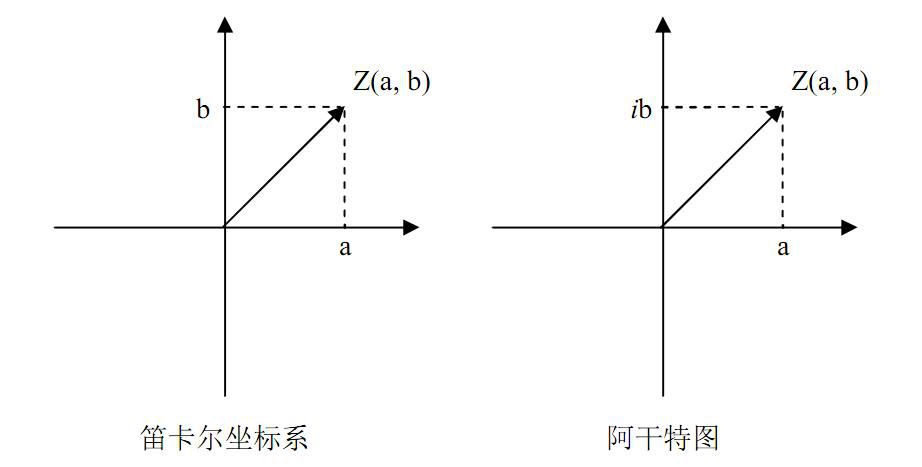
所以任意虚数都可以用z=a+ib的形式表述，把这里ib想象成普通坐标系里的纵坐标y。复数的这种几何表示的概念在1797年由挪威的测量学家维塞尔（Caspar Wessel）提出，随即又经瑞士的藏书家阿干特（Jean-Robert Argand）出书进行讨论并得到了高斯的认同，因此这种坐标几何表示也被称为阿干特图（the Argand diagram），其中a，b都是实数，i是虚数，即-1的平方根。

1.三种表现形式和相关转