第五十天| 123.买卖股票的最佳时机III、188.买卖股票的最佳时机IV

第四十八天| 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II-优快云博客

Leetcode 123.买卖股票的最佳时机III

题目链接：123 买卖股票的最佳时机III

题干：给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

思考：动态规划。本题关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

• 确定dp数组以及下标的含义

由于最多可以进行两笔交易。首先不能按 122.买卖股票的最佳时机II 中每次将利润当作本金处理，因为这无法控制交易的次数，因此考虑将这两次交易细节记录下，考虑以下五种状态：

1. 没有操作 （其实我们也可以不设置这个状态）
2. 第一次持有股票
3. 第一次不持有股票
4. 第二次持有股票
5. 第二次不持有股票

dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。

• 确定递推公式

达到dp[i][1]状态，有两个具体操作：

• 操作一：第i天买入股票，那么dp[i][1] = dp[i-1][0] - prices[i]
• 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]

并且选较大的，所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);

同理dp[i][2]也有两个操作：

• 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
• 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]

所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])

同理可推出剩下状态部分：

dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);

dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

• dp数组如何初始化

状态0表示操作，因此此状态一直为0，则dp[0][0] = 0;

同 121. 买卖股票的最佳时机一样，第0天做第一次买入的操作，dp[0][1] = -prices[0]; 第0天做第一次卖出的操作，dp[0][2] = 0;

至于第0天第二次买入操作，由于第二次买入依赖于第一次卖出的状态，相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;

• 确定遍历顺序

从递归公式可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

• 举例推导dp数组

举例：[3,3,5,0,0,3,1,4]，dp数组状态如下：

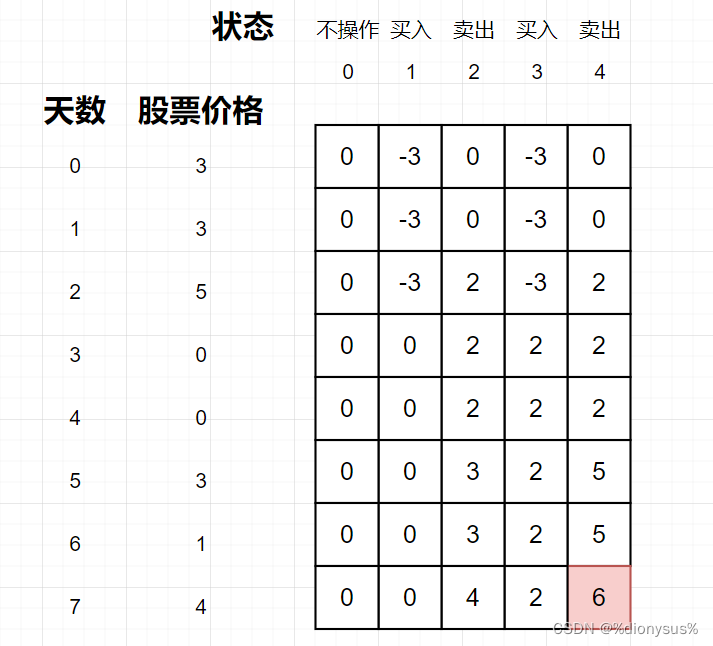
由于第一次卖出股票所得利润当作第二次买入股票的本金，因此最后返回第二次卖出股票所得利润即可。 

代码：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //dp[i][0]:不操作   
        //dp[i][1]:第一次持有股票手上的金额     dp[i][2]:第一次不持有股票手上的金额  
        //dp[i][3]:第二次持有股票手上的金额     dp[i][4]:第二次不持有股票手上的金额
        vector<vector<int>> dp(prices.size(), vector<int>(5));
        dp[0][0] = 0;
        dp[0][1] = - prices[0];
        dp[0][2] = 0;
        dp[0][3] = - prices[0];
        dp[0][4] = 0;

        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = 0;
            dp[i][1] = max(dp[i - 1][1], - prices[i]);                  //之前已买入股票 或 第i天买入股票（第一次）
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);     //之前已卖出股票 或 第i天卖出股票（第一次）
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);     //之前已买入股票 或 第i天买入股票（第二次，第一次利润作本金）
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);     //之前已卖出股票 或 第i天卖出股票（第二次）
        }

        return dp[prices.size() - 1][4];
    }
};

优化：从递推公式可以看出，dp[i]只是依赖于dp[i - 1]的状态。因此只需要记录 当前天的dp状态和前一天的dp状态即可，就是使用滚动数组来节省空间。

代码：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        vector<int> dp(5, 0);
        dp[1] = - prices[0];
        dp[3] = - prices[0];

        for (int i = 1; i < prices.size(); i++) {
            dp[1] = max(dp[1], dp[0] - prices[i]);
            dp[2] = max(dp[2], dp[1] + prices[i]);
            dp[3] = max(dp[3], dp[2] - prices[i]);
            dp[4] = max(dp[4], dp[3] + prices[i]);
        }
        return dp[4];
    }
};

Leetcode 188.买卖股票的最佳时机IV

题目链接：188 买卖股票的最佳时机IV

题干：给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

思考：动态规划。本题和上题思路几乎一样，无非是多加几个状态去记录。

代码：

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        //dp[i][0]:不操作   
        //dp[i][2 * j + 1]:第j次持有股票手上的金额     dp[i][2 * j + 2]:第j次不持有股票手上的金额  
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));

        for (int i = 1; i <= 2 * k; i += 2)     //初始化
            dp[0][i] = - prices[0];

        for (int i = 1; i < prices.size(); i++) {       //遍历天数
            for (int j = 1; j <= 2 * k; j += 2) {       //遍历交易
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);         //之前已买入股票 或 第i天买入股票（第j / 2 + 1次）
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] + prices[i]);     //之前已买入股票 或 第i + 1天买入股票（第j / 2 + 1次，前一次交易利润作本金）
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
};

自我总结：

理解增加dp状态来记录不同次的交易，仅在循环过程中将前一次利润当本金处理不能控制交易次数。