文章目录
逻辑回归
背景
二元分类问题:是否佩戴老花镜与年龄的关系
1.分析
(1)是否佩戴老花镜y(0或1)与年龄x的关系:

(2)设想:y与x的关系用 y =
θ
\theta
θ0 +
θ
\theta
θ1x 来表示
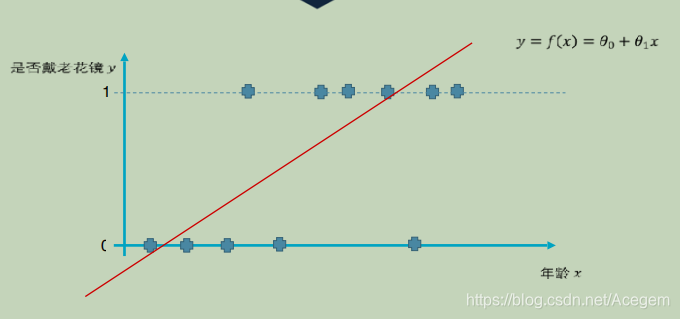
(3)可以看到并不能很好的拟合

2.正解
(4)引入逻辑函数:
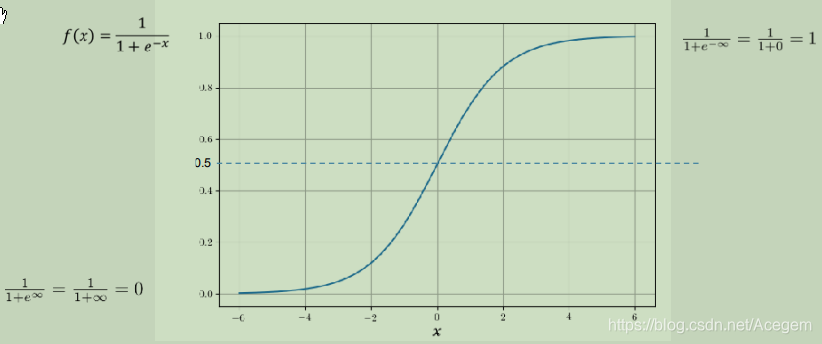
(5)y与x的关系用 y =
θ
\theta
θ0 +
θ
\theta
θ1x 来表示,再经过逻辑函数处理,就能很好地做到二元分类(0或1)。
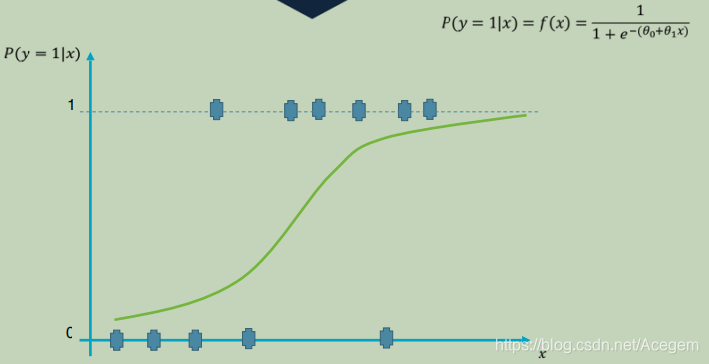
理论

附:
- 指数和对数
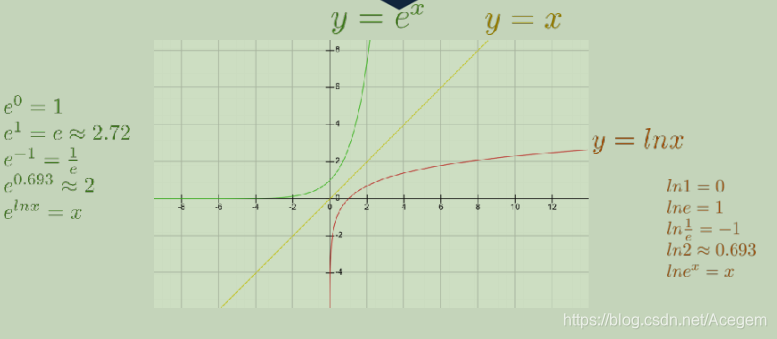
- 小知识点

实例
已知一些样本数据如下:年龄和年收入 与 是否买车的关系
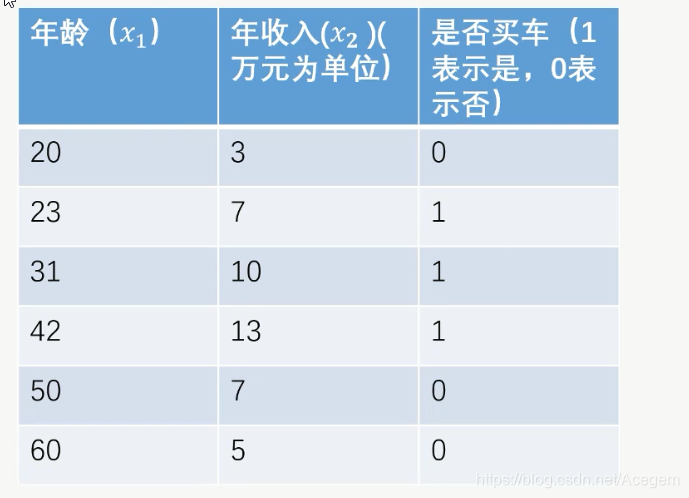
问:有一年龄28、年收入8万的人,预测其是否买车?买车概率多大?
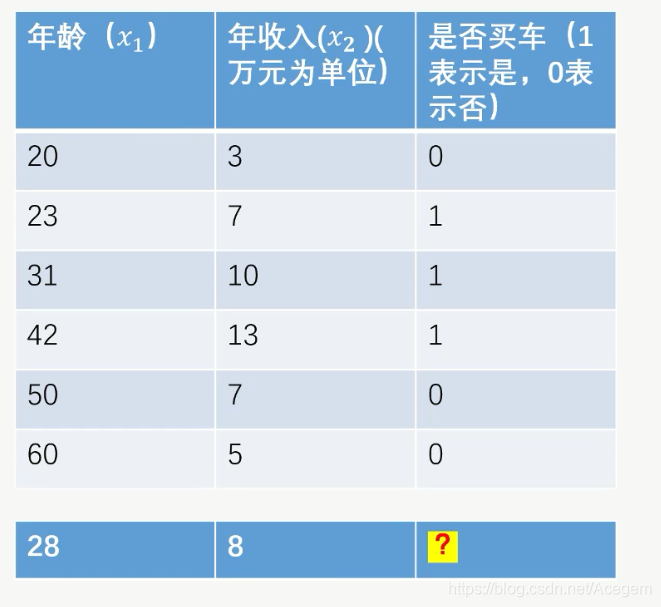
利用逻辑回归训练模型,代码如下:
from sklearn import linear_model
X = [
[20, 3],
[23, 7],
[31, 10],
[42, 13],
[50, 7],
[60, 5]
]
y = [
0,
1,
1,
1,
0,
0
]
lr = linear_model.LogisticRegression()
lr.fit(X, y)
testX = [
[28, 8]
]
label = lr.predict(testX)
# 预测类别标签:[1或0] 即 [买车/不买车]
print("predicted label = ", label)
# 预测概率:[o的概率 1的概率]
prob = lr.predict_proba(testX)
print("probalility = ", prob)
运行结果:
predicted label = [1]
probalility = [[0.14694811 0.85305189]]
可以看到:
testX = [[28, 8]] ---- 年龄28年收入8万的人
predicted label = [1] ----- 预测结果是1,即买车
probalility = [[0.14694811 0.85305189]] ----- 不买车概率是0.14694811,买车概率是0.85305189
损失函数
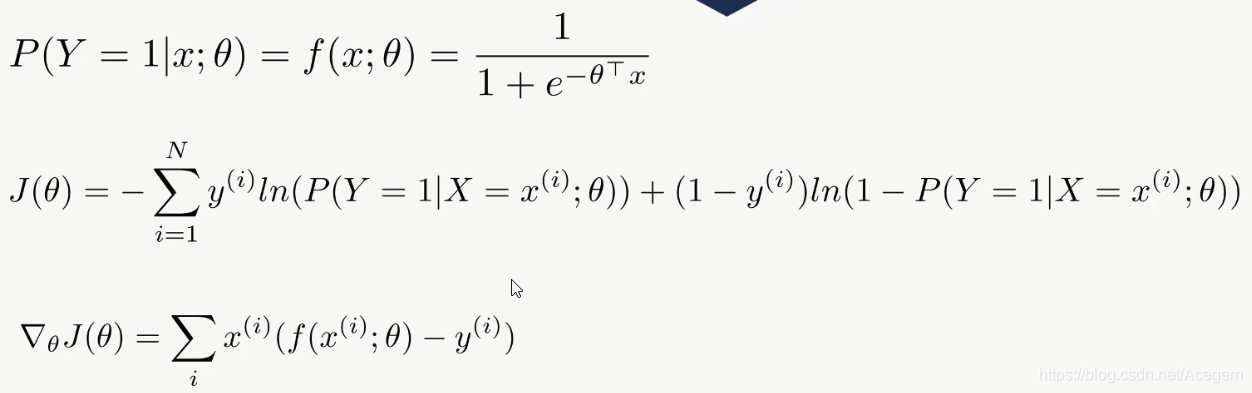
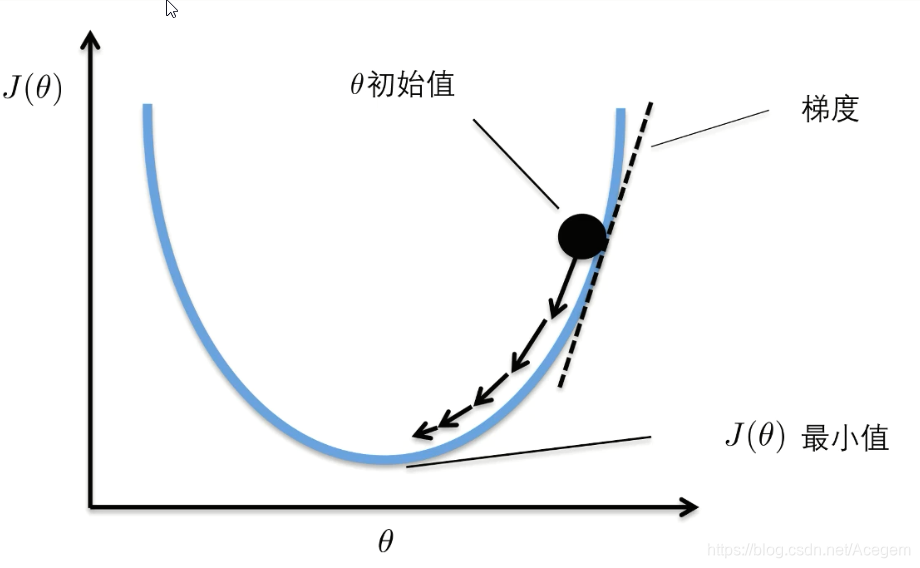
 逻辑回归应用实例
逻辑回归应用实例







 本文探讨了逻辑回归在二元分类问题中的应用,通过分析年龄、年收入与是否买车的关系,展示了如何使用逻辑回归进行预测,并提供了详细的代码示例。
本文探讨了逻辑回归在二元分类问题中的应用,通过分析年龄、年收入与是否买车的关系,展示了如何使用逻辑回归进行预测,并提供了详细的代码示例。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








