Deep Learning 笔记（1）：神经网络和深度学习的初体验

本文链接：https://blog.youkuaiyun.com/Abandon_first/article/details/119384720

什么是神经网络？

房屋预测例子：
输入为特征，比如 size、bedrooms、zip code 等，经过全连接网络，输出房屋价格。
在这里插入图片描述

用神经网络进行监督学习

可以进行多种类型的任务，比如估计房价、网络广告、标记图片、语音识别、机器翻译、自动驾驶，所使用的网络种类涵盖了 standard NN、CNN、RNN 和自定义多模态网络。
在这里插入图片描述
所涉及的数据也可以划分为结构化数据表格和非结构化数据图像、语音、文字等。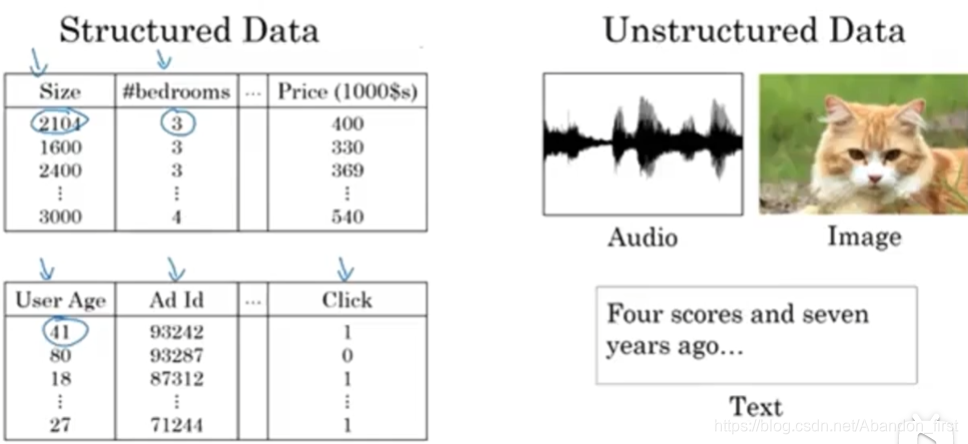

为什么深度学习会兴起

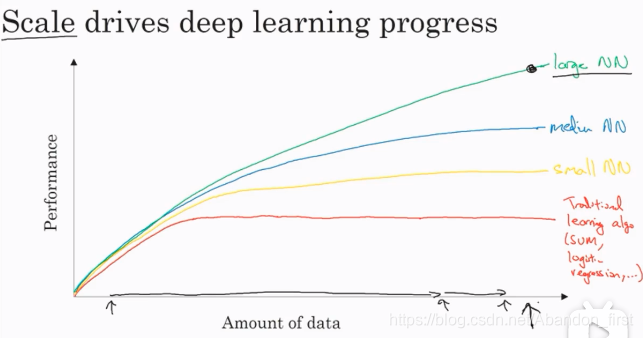
随着大数据时代的到来，深度学习逐渐成为主流。可以理解为，深度学习神经网络的模型表达能力一般优于甚至远远优于传统的机器学习模型，模型参数也大大增加，这是两者各自拥有的特点。当数据量不够的时候，训练神经网络非常容易过拟合，而训练传统的机器学习模型却比较适合。随着数据量尤其某些任务的已标注的数据越来越多时，训练神经网络会比训练传统机器学习模型的收益高得多。
在这里插入图片描述

二分分类

在神经网络的推导过程中，一张图片/样本 flatten 成一个列向量后，然后横向堆叠为矩阵，也就是 m 个样本，特征向量大小为 n（特征空间是 n 维），会堆叠成一个 n 行 m 列的输入矩阵（我不是很喜欢这种，我喜欢 m 行 n 列的……）；在此种约定下，每个样本的标记 y 是个 1 行 m 列的矩阵。

多说两句吧，我喜欢 m 行 n 列的是因为矩阵分析中都是以矩阵 A 行为样本数，列为特征数，对矩阵 A 的空间进行操作是右乘列向量比如 $A x = y$ 这么个样子。但是此处用 n 行 m 列，其实是更方便去写 $y = k x + b$ （这么写不严谨，就这么个意思就行）。但其实本质是等价的。
在这里插入图片描述

logistic 回归

给定 n 维特征空间的一个样本 $\in \mathcal{R}^n_x$ （列向量），想求该样本是一只猫的概率为 $\hat y$ （条件概率），模型参数 $\in \mathcal{R}^n_x$ （列向量）， $\in \mathcal{R}$ （计算时可以把 w 和 b 放在一起作为 $\Theta$ ）。那么有：

在这里插入图片描述

logistic 回归损失函数

朴素地来说，我们希望对于样本数量为 m 的数据集中，预测结果尽可能的接近真实结果。为了训练模型或者说学习到参数，我们需要一个函数来衡量预测与真实结果之间的差异。

这种函数可以有很多，比如均方差函数，但是此处使用 MSE 效果并不好。二分类问题一般使用二值交叉熵损失函数 binary cross entropy，BCE，如下图 $\mathcal{L}(\hat y, y)$ 。而对于整个样本数据集来说，损失函数就变成了下图中的 $J (w, b)$ 。

而所谓的训练学习过程，就是找到那么一组参数 w 和 b，应用在样本集上，使得 $J (w, b)$ 最小。
在这里插入图片描述

梯度下降法

学习率为 $\alpha$ ，不断地更新参数，直到到达最优解（当然是全局最优解最好）。
在这里插入图片描述

计算图

本图为前向计算。
在这里插入图片描述

使用计算图求导

链式法则反向求导。
在这里插入图片描述

logistic 回归中的梯度下降

针对单个样本 $x = [x_1, x_2]^T$ ，参数 $w = [w1, w2]^T$ ，以及 loss function 上计算。
$W^T \cdot X = [w_1, w_2, b] \cdot [x_1, x_2, 1]^T = w_1 x_1 + w_2 x_2 + b$

$\hat y = a = \sigma(z)$

$\mathcal{L}(\hat y, y) = -[y lg \hat y + (1-y) lg (1 - \hat y)]$

$\mathcal{L}$ 对 $\hat y$ 求导结果为 $-\frac{y}{\hat y} + \frac{1 - y}{1 - \hat y}$

sigmoid 函数求导为 $\hat y * (1 - \hat y)$

z 对 $w_1$ 求导为 $x_1$ 。

在这里插入图片描述

m 个样本的梯度下降

对于 m 个样本来说，要在 cost function 上计算过程如下图。图中是通过显式地 for 循环来计算权重导数继而进行更新的。后面就会讲到向量化地方式来进行计算，因为数据量太大了，矩阵要用起来了，不然无论是编程代码还是实际运行效率都起不来。
在这里插入图片描述

向量化 logistic 回归

不使用 for 循环等。
在这里插入图片描述

向量化 logistic 回归的梯度输出

向量化求梯度。
在这里插入图片描述

logistic 损失函数的解释

在这里插入图片描述

神经网络概览

下图是个两层的神经网络，每个节点运算后都有非线性的，其实就是多层感知机了。图中也包括了前向预测和反向传播。
在这里插入图片描述

计算神经网络的输出

对于单个样本，有 3 个特征，隐藏层 4 个单元的情况，计算如下。上标表示层数，此时第 1 层中各个神经元对应的权重 $w^[1]_i$ 都被转置后一行行放在一起为矩阵 W，每行对应一个神经元，所以后面直接写 W × X 而不需要再加转置。列数对应样本数，行数对应特征数。
在这里插入图片描述

多个样本的向量化

向量化实现的解释

激活函数

sigmoid 简单，输出范围 0 到 1，还适合当门，但是除了二分类问题的输出层以外，几乎不用， $\frac{1}{1 + e^{-x}}$ ，导数 $y^{'} = y (1 - y)$ 。
tanh 比 sigmoid 更好，输出范围 -1 到 1，很适合特征操作， $\frac{e^x - e^{-x}}{e^x + e^{-x}}$ ，导数 $y' = 1 - y^2$ 。
常用 Relu 或者 Leaky Relu，虽然左边被抑制了，但是并没什么太大问题，因为神经网络参数实在太多了，部分抑制倒是件好事（有点 dropout 的意思了吧）。

为什么需要非线性激活函数

默认激活函数指的是非线性激活函数。如果没有激活函数，那么模型的能力就只有线性，只能对特征进行线性操作，无论你叠加多少层都是一样的。简单的例子，没有激活函数，异或问题都解决不了。

神经网络的梯度下降法和反向传播

这里我自己写一遍吧，TODO。顺便写一下为啥初始化不能全为 0。（记得吧，因为更新量是负学习率乘以导数，然后那个导数，最前面的 w 的导数和输入有关，中间 w 的导数和对应节点值要乘积的，如果权重最开始都为 0 ，那么更新不了。）

随机初始化

老师这里说的是，如果全都为 0，那么同一层上的神经元就完全对称，一模一样，一开始做的操作一模一样，对输出的影响也一模一样，反向传播的时候也一模一样，多个隐藏层单元的设计也就毫无意义了。所以 w 的初始化必须是随机的，可以是比较小的随机值，这样刚刚开始学习的时候，落在激活函数中间部分，这样比较容易更新（反之梯度消失）。而 b 不存在什么对称性问题，所以 b 完全可以初始化为 0。

所以正则化也是惩罚权重的绝对值太大，惩罚他们去激活函数的两侧陷入平坦区而无法进一步学习。