树状数组

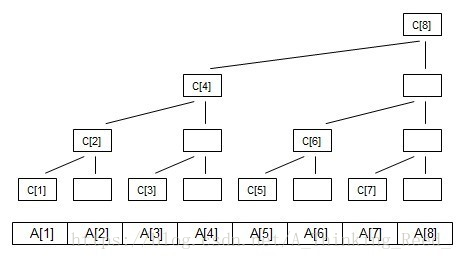
C[i]代表每个节点下子节点权值之和

 

由图可知：
C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

 

化为二进制表示：

 

1=(001)      C[1]=A[1];

2=(010)      C[2]=A[1]+A[2];

3=(011)      C[3]=A[3];

4=(100)      C[4]=A[1]+A[2]+A[3]+A[4];

5=(101)      C[5]=A[5];

6=(110)      C[6]=A[5]+A[6];

7=(111)      C[7]=A[7];

8=(1000)    C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

 

得 ：C[i]=A[i-k+1]+A[i-k+2]+......+A[i];
(k为i的二进制中位于最低位的1代表的数)
例如当i=8(1000), k=8;
       当i=7(111),   k=1;

 

引入lowbit(x) = k

int lowbit(x)

{
    return x&(-x);
}

证明lowbit()：
首先明白一个概念，计算机中-i=（i的取反+1），也就是i的补码 
而lowbit，就是求（树状数组中）一个数二进制的1的最低位，例如01100110，lowbit=00000010；再例如01100000，lowbit=00100000。 
所以若一个数（先考虑四位）的二进制为abcd，那么其取反为(1-a)(1-b)(1-c)(1-d)，那么其补码为(1-a)(1-b)(1-c)(2-d)。 
如果d为1，什么事都没有-_-|||但我们知道如果d为0，天理不容2Σ( ° △ °|||)︴ 
于是就要进位。如果c也为0，那么1-b又要加1，然后又有可能是1-a……直到碰见一个为补码为0的bit，我们假设这个bit的位置为x 
这个时候可以发现：是不是x之前的bit的补码都与其自身不同？，x之后的补码与其自身一样都是0？ 
例如01101000，反码为10010111，补码为10011000，可以看到在原来数正数第五位前，补码的进位因第五位使其不会受到影响，于是0&1=0,； 
但在这个原来数“1”后，所有零的补码都会因加1而进位，导致在这个“1”后所有数都变成0，再加上0&0=0，所以他们运算结果也都是零； 
只有在这个数处，0+1=1，连锁反应停止，所以这个数就被确定啦O(∩_∩)O 
所以and以后只有x这个bit是一……
 

单点更新：每插入或更新一个节点，与之有关的节点的数随之改变
代码：

void add(int x, int y)         ///将第x个数加y
{
    for(int i=x; i<=n; i+=lowbit(i))
        tree[i] += y;
}

举例：

当更新A[3]时  需要向上更新C[3],C[4],C[8]

写为二进制  C[(010)],C[(100)],C[(1000)]

                            3(011)                          C[3]+=A[3]

lowbit(3)=001     3+lowbit(3)=4(100)     C[4]+=A[3]

lowbit(4)=100     4+lowbit(4)=8(1000)   C[8]+=A[3]

区间查询代码：

int getsum(int x)              ///前x个数的和
{
    int ans = 0;
    for(int i=x; i>0; i-=lowbit(i))
        ans += tree[i];
    return ans;
}
int ask(int l, int r)          ///l~r区间和
{
   return getsum(r) - getsum(l-1);
}

举例：

对getsum(7)：

                         7(111)                        ans+=C[7]

lowbit(7)=001  7-lowbit(7)=6(110)    ans+=C[6]

lowbit(6)=010  6-lowbit(6)=4(100)    ans+=C[4]

lowbit(4)=100  4-lowbit(4)=0(000)    

完整代码

#include <cstdio>
#include <iostream>
using namespace std;
int tree[1000001], n;
int lowbit(int t)
{
    return t&(-t);
}
void add(int x, int y)         ///将第x个数加y
{
    for(int i=x; i<=n; i+=lowbit(i))
        tree[i] += y;
}
int getsum(int x)              ///前x个数的和
{
    int ans = 0;
    for(int i=x; i>0; i-=lowbit(i))
        ans += tree[i];
    return ans;
}
int ask(int l, int r)          ///l~r区间和
{
    return getsum(r) - getsum(l-1);
}
int main()
{
    while(cin >> n)
    {
        for(int i=1; i<=n; i++)
        {
            int temp;
            cin >> temp;
            add(i, temp);
        }
        int l, r;
        while(scanf("%d%d", &l, &r) && l+r)
        {
            cout << ask(l, r) << endl;
        }
    }
}