LeetCode96题：不同的二叉搜索树

思路：

一般来说，只要涉及到二叉树或二叉搜索树的，基本都要用到根结点和递归的思想。对于本题来说，假设要求的结果为f(n)，那么开始分析：由1到n节点组成的二叉搜索树的根结点总共有n种取值情况，即1,2...n分别作为根结点，当1作为根结点时，其左子树为空记为f(0)，右子树为2到n总共n-1个节点组成的二叉搜索树，且这n-1个节点总共有f(n-1)种组成情况，因此，以1为根结点时，总共有f(0)*f(n-1)种不同的二叉搜索树（令f(0)=1）；同理，以2为根结点时，左子树只有1这一个节点，所以f(1)=1，总共有f(1)*f(n-2)种组成情况。。。，很明显是递归的过程。最终的结果表达式为：f(n) = f(0)*f(n-1)+f(1)*f(n-2)+...+f(n-1)*f(0)。

 

解法一：递归

public int numTrees(int n) {
	if(n <= 1)
		return 1;
	int res = 0;
	for(int i=0;i<n;i++){
		res += numTrees(i)*numTrees(n-1-i);
	}
	return res;
}

递归不出意料的出现了超时问题，因为有重复计算，因此想到用map保存已知的结果f(i)来优化算法，即动态规划的思想。

 

解法二：map实现动态规划

static Map<Integer,Integer> map = new HashMap<>();
public int numTrees(int n) {
    if(n <= 1){
        return 1;
    }
    int res = 0;
    if(map.containsKey(n)){
        return map.get(n);
    }else{
        for(int i=0;i<n;i++){
            res += numTrees(i)*numTrees(n-1-i);
        }
        map.put(n,res);
    }
    return res;
}

下面是n=20时，两种算法耗时对比：

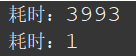
但是在LeetCode中大概耗时3ms，只能击败7%的提交。

LeetCode上还有一种使用数组实现的动态规划的解法，只需要0ms，没太理解，这里只贴出代码。

public int numTrees(int n) {
    int[] G = new int[n + 1];
    G[0] = 1;
    G[1] = 1;
    for (int i = 2; i <= n; ++i) {
      for (int j = 1; j <= i; ++j) {
        G[i] += G[j - 1] * G[i - j];
      }
    }
    return G[n];
}

 

解法三：卡特兰数数列

卡特兰数是组合数学中一个常出现在各种计数问题中的数列。其满足如下条件：f(0) = 1,f(1) = 1,f(n) = f(0)*f(n-1)+f(1)*f(n-2)+...+f(n-1)*f(0)。通过分析可知，此题就是一个卡特兰数列求第n项的问题。而卡特兰数列的另一个递推公式为：f(n)=f(n-1)*(4*n-2)/(n+1)，因此可以直接根据递推公式迭代求解。

public int numTrees(int n) {
    long res = 1;
    for (int i = 1; i <= n; i++) {
        res = res * (4 * i - 2) / (i + 1);
    }
    return (int) res;
}