二叉树的镜像
题目描述:
请完成一个函数,输入一棵二叉树,该函数输出它的镜像。
输入描述:
二叉树的镜像定义:源二叉树
8
/ \
6 10
/ \ / \
5 7 9 11
镜像二叉树
8
/ \
10 6
/ \ / \
11 9 7 5
其实就是交换二叉树的左右子树,可用递归实现:
交换根节点的左右孩子,再分别对左孩子进行镜像和右孩子进行镜像
我的代码(Java):
package jianzhioffer;
import java.util.Scanner;
public class MirrorRecursively {
/**
* 二叉树节点的定义
*/
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode righe = null;
public TreeNode(int val) {
this.val = val;
}
}
/**
* 根据树的前序遍历和中序遍历重建二叉树
*/
public BinaryTreeNode reContructionTree(int[] pre, int[] in) {
if (pre.length == 0 || in.length == 0) {
return null;
}
BinaryTreeNode root = binaryTreeContruction(pre, 0, pre.length - 1, in, 0, in.length - 1);
return root;
}
private BinaryTreeNode binaryTreeContruction(int[] pre, int startPre, int endPre, int[] in, int startIn, int endIn) {
if (startIn > endIn || startPre > endPre) {
return null;
}
BinaryTreeNode node = new BinaryTreeNode(pre[startPre]);
for (int i = startIn; i <= endIn; i++) {
if (in[i] == pre[startPre]) {
node.left = binaryTreeContruction(pre, startPre + 1, startPre + i - startIn, in, startIn, i - 1);
node.right = binaryTreeContruction(pre, i - startIn + startPre + 1, endPre, in, i + 1, endIn);
}
}
return node;
}
/**
* 中序遍历
*
* @param root
*/
private void LDRPrint(BinaryTreeNode root) {
if (root == null) {
return;
} else {
LDRPrint(root.left);
System.out.print(root.val + " ");
LDRPrint(root.right);
}
}
/**
* 前序遍历
*/
private void DLRPrint(BinaryTreeNode root) {
System.out.print(root.val + " ");
BinaryTreeNode leftTree = root.left;
if (leftTree != null) {
DLRPrint(leftTree);
}
BinaryTreeNode rightTree = root.right;
if (rightTree != null) {
DLRPrint(rightTree);
}
}
/**
* 二叉树的镜像:递归实现
*
* @param root
*/
private void mirrorRecursively(BinaryTreeNode root) {
if (root == null)
return;
if (root.left == null && root.right == null)
return;
BinaryTreeNode pTemp = root.left;
root.left = root.right;
root.right = pTemp;
if (root.left != null) {
mirrorRecursively(root.left);
}
if (root.right != null) {
mirrorRecursively(root.right);
}
}
/**
* 二叉树的镜像:非递归实现
*
* @param root
*/
public void mirrorRecursively1(BinaryTreeNode root) {
if (root == null) {
return;
}
//借助于辅助栈
LinkedList<BinaryTreeNode> stack = new LinkedList<BinaryTreeNode>();
//存放出栈的栈顶元素
BinaryTreeNode current = null;
BinaryTreeNode temp = null;
//将根元素入栈
stack.push(root);
while (!stack.isEmpty()) {
//将根元素出栈 交换根元素的左右子树
current = stack.pop();
//若左右孩子不为空则交换左右孩子
if (current.left != null || current.right != null) {
temp = current.left;
current.left = current.right;
current.right = temp;
}
//将根元素的左右孩子压入栈中
if (current.left != null)
stack.push(current.left);
if (current.right != null)
stack.push(current.right);
}
}
//创建整型数组
public static int[] nodeProcess(String[] array) {
int[] num = new int[array.length];
for (int i = 0; i < array.length; i++) {
num[i] = Integer.parseInt(array[i]);
}
return num;
}
/**
* 主函数
* 输入两行,分别表示树的前序遍历和中序遍历
*
* @param args
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
String[] preStr = sc.nextLine().split(",");
String[] inStr = sc.nextLine().split(",");
int[] pre = nodeProcess(preStr);
int[] in = nodeProcess(inStr);
MirrorRecursively mr = new MirrorRecursively();
BinaryTreeNode root = mr.reContructionTree(pre, in);
mr.mirrorRecursively(root);
mr.DLRPrint(root);
System.out.println();
mr.LDRPrint(root);
}
sc.close();
}
}
测试:
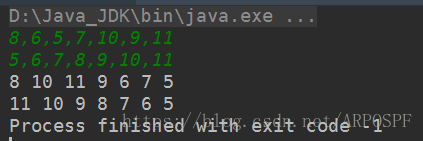








 本文介绍了一种通过递归和非递归方法实现二叉树镜像的技术。递归方法通过交换根节点的左右子树并递归地对子树进行相同操作来完成;非递归方法使用栈来逐层遍历树并交换节点的子树。
本文介绍了一种通过递归和非递归方法实现二叉树镜像的技术。递归方法通过交换根节点的左右子树并递归地对子树进行相同操作来完成;非递归方法使用栈来逐层遍历树并交换节点的子树。

















 162
162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










