剑指offer二叉树镜像

题目：

操作给定的二叉树，将其变换为源二叉树的镜像。

 解读：

• 从树的根节点开始遍历，遍历到根节点，然后看有没有左右子节点，如果有的话，交换他们的左右位置
• 递归遍历，对于每一个节点，遍历它的子节点，如果存在即交换位置，直到遍历到没有子节点为止

如下图所示，形象表述了镜像的整个过程，对于镜像操作，有两种方案，一种是使用递归的方式，一种是非递归方式，前者较简单一些，后者稍微复杂。

 

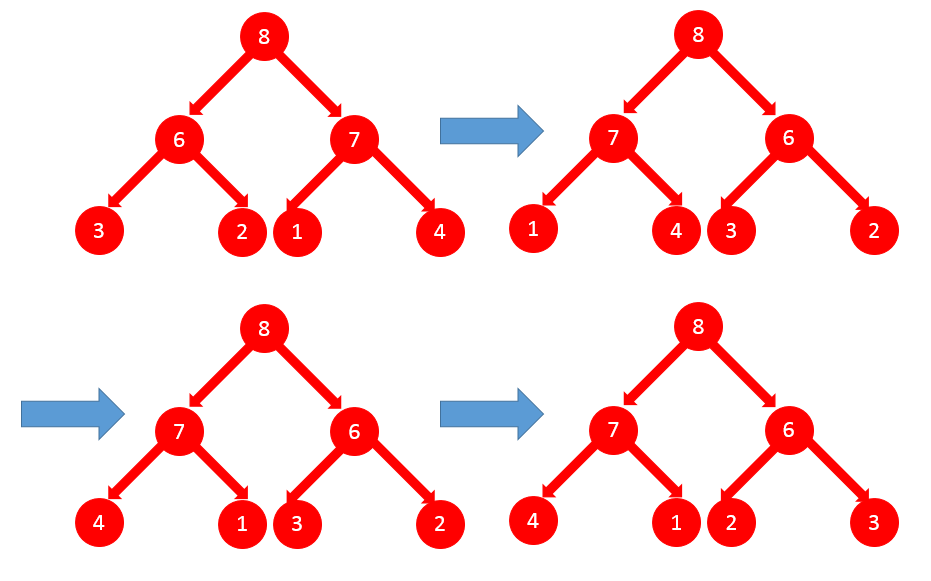
递归代码：

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    void Mirror(TreeNode *pRoot) {
              if(pRoot) 
              {
                TreeNode *temp = pRoot->left;
                pRoot->left = pRoot->right;
                pRoot->right = temp;
                Mirror(pRoot->left);
                Mirror(pRoot->right);
              }
    }
    
};

 

 

非递归代码： 

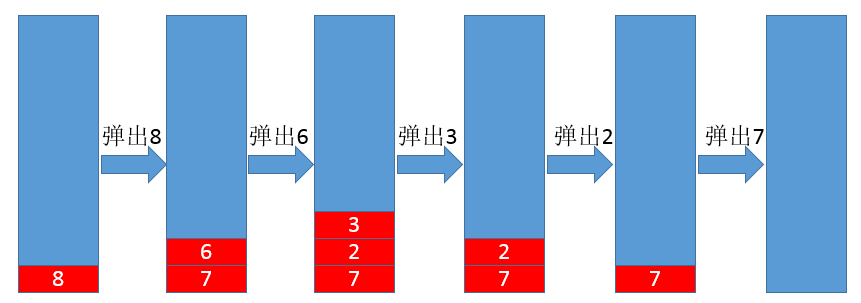
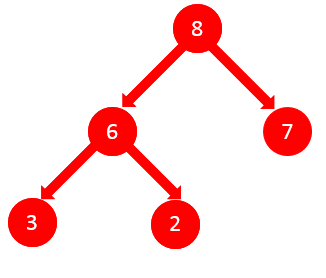
解释：给定如下一个二叉树，用非递归法进行镜像，这种方法是基于栈的DFS（深度优先搜索）来遍历的，这种方法其实主要运用了树的先序搜索方法，对于先序搜索，这里用基于栈的先序搜索说明下图所示的树:

• 先把数据8进入栈中，进入之后弹出栈顶元素8
• 分别把弹出元素（如果存在）的右子节点和左子结点压入栈中，进入之后弹出，这里是进入7、6，弹出了栈顶6
• 继续按上述操作，弹出6之后，压入2、3，进入后，弹出3，3没有左右子节点，弹出栈顶2，2也没有左右子节点，弹出7
• 弹出顺序是8、6、3、2、7

对于如下一个稍微大的树，基于栈用先序搜索，步骤如下：

 

 

/*
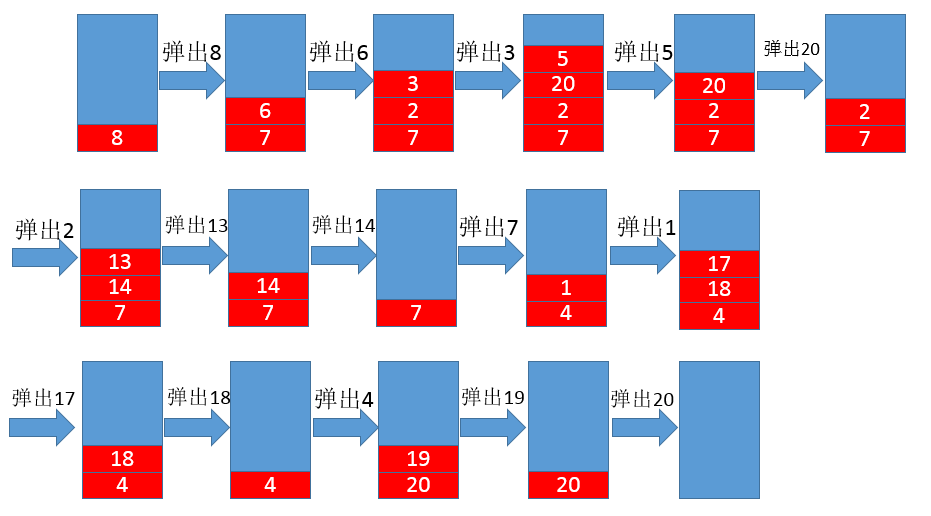
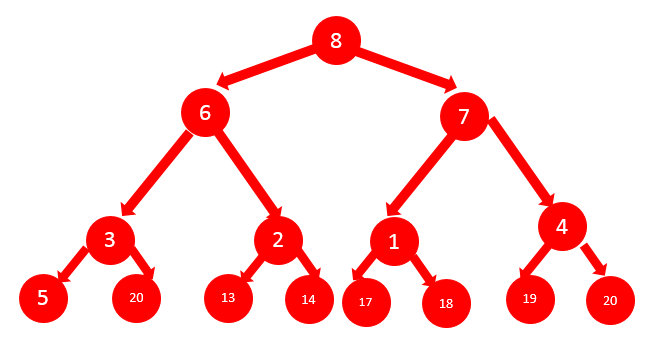
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    void Mirror(TreeNode *pRoot) {

        if(!pRoot) 
        {
            return;
        }
        stack<TreeNode*> stack;
        stack.push(pRoot);//首先压入根节点
        while(!stack.empty()) //知道栈内元素为空，结束循环
        {
            TreeNode *node = stack.top();//弹出栈顶元素，下面三步交换弹出元素的左右子节点
            stack.pop();
            TreeNode *temp = node->left;
            node->left = node->right;
            node->right = temp;
            if(node->left) //交换完后，如果存在左子节点，把该节点压入栈
            {
                stack.push(node->left);
            }
            if(node->right) //交换完后，如果存在右子节点，把该节点压入栈
            {
                stack.push(node->right);
            }
        }
    }
    
};