【强化学习】强化学习数学基础：Actor-Critic方法

Actor-Critic方法是一个非常重要的policy gradient methods。这一类方法强调的一种整合策略梯度和value-based方法的结构。
什么是“ actor”和“ critic”？

• “actor”表示policy update。它被称为actor是因为policies will be applied to take actions。
• “critic”表示policy evaluation或者value estimation。它被称为critic是因为it criticizes the policy by evaluating it。

1. The simplest actor-critic(QAC)

重新回顾policy gradient的思想：

我们可以从这个算法中看到“actor”和“critic”：

• 这个算法对应actor！
• 这个算法估计$q_t(s_t,a_t)$对应ctitirc！$q_t$是$q_{\pi }$的近似

如何得到$q_t(s_t,a_t)$？到目前为止，我们已经学习过两种方法来估计action values：

现在给出第一个Actor-Critic算法：QAC

对上面算法做一些补充说明：

• critic对应“Sarsa+value function approximation”
• actor对应policy update algorithm.
• 这个算法是on-policy，为什么呢？
  • 因为这个policy是stochastic，no need to use techniques like $ϵ$-greedy
• 这个特殊的actor-critic algorithm有时候也被称为Q Actor-Critic（QAC）。
• 尽管简单，但是该算法揭示了actor-critic方法的核心思想。它可以被扩展到其他算法当中。

2. Advantage actor-critic(A2C)

A2C是QAC的一个推广。基本思想是它在reduce variance过程中引入了一个baseline。

Baseline invariance

首先介绍一个性质，the policy gradient is invariant to an additional baseline：

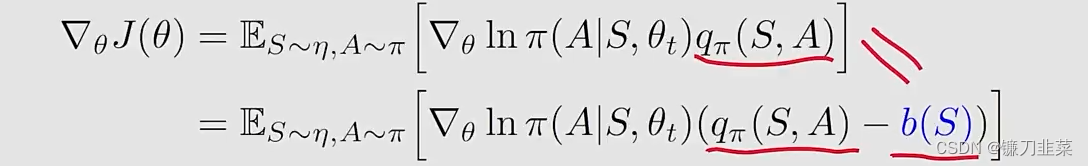
这里，the additional baseline $b(S)$ 是$S$的一个scale function。

两个问题：

1. 为什么引入一个新的b(S)它不会发生变化？
2. 为什么要关注这个$b(S)$，它究竟有什么用？

第一个问题，为什么引入一个新的$b(S)$公式仍然成立？这是因为

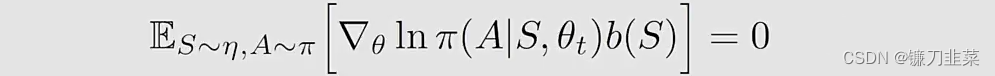
细节如下：

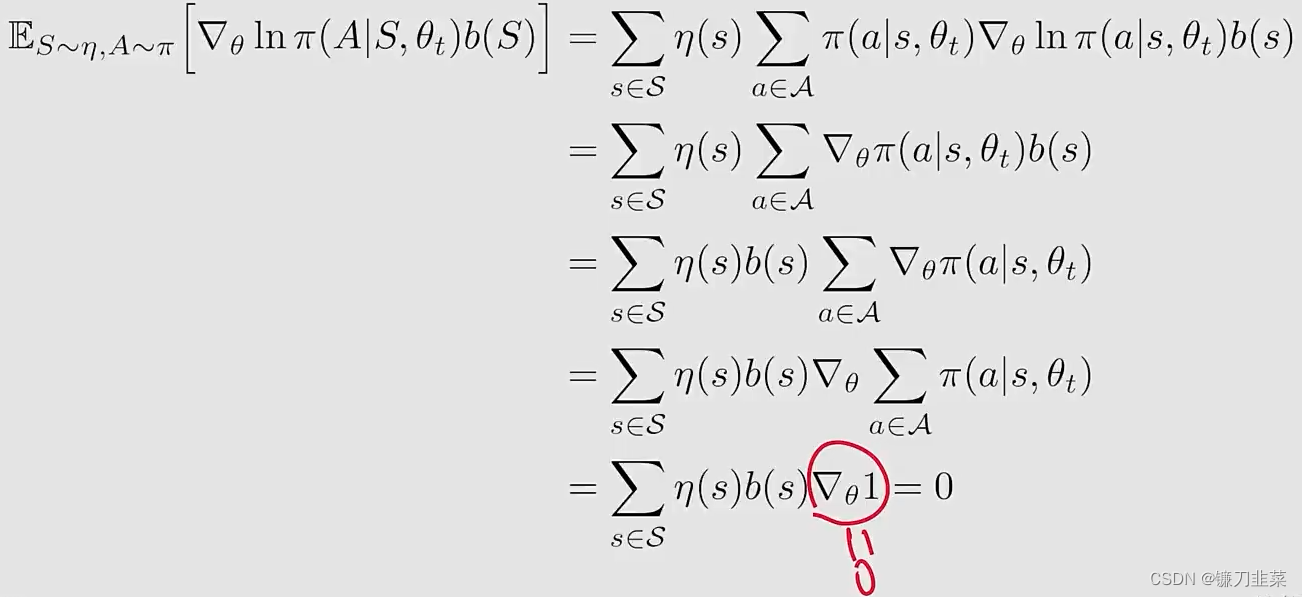
第二个问题，为什么这个baseline是有用的？首先把刚才的这个梯度${\nabla }_{\theta }J(\theta )=\mathbb{E}[X]$，把这个$\mathbb{E}[X]$写成一个新的变量$X$：

我们有：

• $\mathbb{E}[X]$对于$b(S)$是invariant
• 方差$var(X)$对于$b(S)$不是invariant
  • 为什么？因为$tr[var(X)]=\mathbb{E}[X^T-X]-{\bar{x}}^T\bar{x}$，并且
    
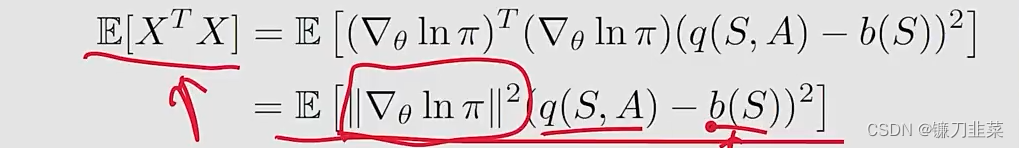
    当b是非常巨大的时候，对于E的影响也是不一样的。

我们的目标：寻找一个最优的baseline $b$最小化$var(X)$

• Benefit：当我们使用一个随机采样去近似$\mathbb{E}[X]$的时候，the estimation variance应当是较小的。

在REINFORCE和QAC算法中：

• 没有baseline
• 或者，我们可以说$b=0$，也就是not guaranteed to be a good baseline。

能够最小化方差$var(X)$的最优baseline应当是，对于任意$s\in \mathcal{S}$，有

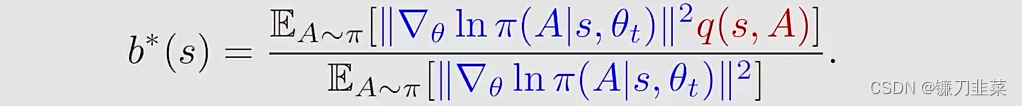
• 尽管这个baseline是最优的，但是它太复杂了
• 所以，我们可以移除权重$||{\nabla }_{\theta }\ln \pi (A|s,{\theta }_t)|{|}^2$并且选择次优的baseline：$$b(s)={\mathbb{E}}_{A\sim \pi }[q(s,A)]=v_{\pi }(s)$$这是s的state value！

The algorithm of advantage actor-critic

当$b(s)=v_{\pi }(s)$，

• the gradient-ascent algorithm是：
  
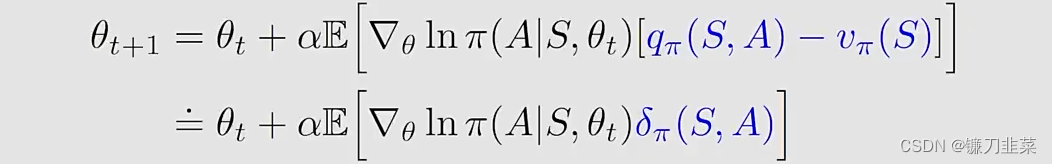
  其中$${\delta }_{\pi }(S,A)\doteq q_{\pi }(S,A)-v_{\pi }(S)$$被称为advantage function（为什么称为advantage？其实它描述的是$q_{\pi }$和$v_{\pi }$之间的差，而$v_{\pi }$是$q_{\pi }$在某一个状态下它的一个平均值，那么如