1. 赛题理解
1.1 背景
火力发电的基本原理是:燃料在燃烧时加热水生成蒸汽,蒸汽压力推动汽轮机旋转,然后汽轮机带动发电机旋转,产生电能。在这一系列的能量转化中,影响发电效率的核心是锅炉的燃烧效率,即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多,包括锅炉的可调参数,如燃烧给量,一二次风,引风,返料风,给水水量;以及锅炉的工况,比如锅炉床温、床压,炉膛温度、压力,过热器的温度等。
1.2 目标
经脱敏后的锅炉传感器采集的数据(采集频率是分钟级别),根据锅炉的工况,预测产生的蒸汽量。
1.3 数据概览
1. 数据描述
数据下载地址:工业蒸汽量预测
2. 数据说明
数据分成训练数据(train.txt)和测试数据(test.txt),其中字段”V0”-“V37”,这38个字段是作为特征变量,”target”作为目标变量。

利用训练数据训练出模型,预测测试数据的目标变量,排名结果依据预测结果的MSE(mean square error)。
1.4 评估指标
预测结果以均方误差MSE(Mean Squared Error)作为评判标准。计算公式如下:
M
S
E
=
S
S
E
n
=
1
n
∑
i
=
1
n
w
i
(
y
i
−
y
^
i
)
2
MSE=\frac{SSE}{n}=\frac{1}{n}\sum_{i=1}^n w_i(y_i-\hat{y}_i)^2
MSE=nSSE=n1i=1∑nwi(yi−y^i)2
其中
y
i
y_i
yi是真实值,
y
^
i
\hat{y}_i
y^i是预测值。
MSE是衡量“平均误差”的一种较为方便的方法。MSE值越小,说明预测模型描述数据具有越高的准确度。在sklearn中可以直接调用mean_squared_error函数计算MSE。调用方法如下:
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,t_predict)
1.5 赛题模型
在赛题分析中,很重要的一点就是要根据赛题的特点和目标明确问题的类型,并选择合适的模型。在机器学习中,根据问题类型的不同,常用的模型包括回归预测模型和分类预测模型
1. 回归预测模型
回归预测模型的预测结果是一个连续值域上的任意值,回归可以具有实值或离散的输入变量。我们通常把多个输入变量的回归问题称为多元回归问题,输入变量按时间排序的回归问题称为时间序列预测问题。
2. 分类预测模型
分类预测模型的分类问题要求将实例分为两个或多个类中的一个,并具有实值或离散的输入变量。其中,两个类别的问题通常被称为二类分类问题或二元分类问题,多于两个类别的问题通常被称为多类别分类问题。
3. 解题思路
在本赛题中,需要用到V0-V37共38个特征变量来预测蒸汽量的数值,数值是一个连续值域上的任意值,故此问题用回归预测算法求解。
回归预测模型使用的算法包括线性回归(Linear Regression)、岭回归(Ridge Regression)、LASSO(Least Absolute Shrinkage and Selection Operator)回归、决策树回归(Decision Tree Regression)、梯度提升树回归(Gradient Boosting Decision Tree Regressor)。
在后面的模型训练中,我们将采用这些模型来预测目标值。
2. 数据探索
2.1 理论知识
2.1.1 变量识别
变量识别就是对数据从变量类型,数据类型等方面进行分析。可以从以下方面对其进行变量识别:
1. 输入变量与输出变量
输入变量(predictor或特征):V0~V37
输出变量(target或标签):target
2. 数据类型
字符型数据有:这里没有字符型数据
数据值数据有:V0~V37,target
3. 连续型变量与类别型变量
连续型变量(特征):V0~V37, target
类别型变量(特征):无
2.1.2 变量分析
1. 单变量分析
对于连续型变量,需要统计数据的中心分布趋势和变量的分布:
| Central Tendency (中心分布趋势) | Measure of Description (离散程度) | Visualization Methods (可视化方法) |
|---|---|---|
| Mean (均值) | Range | Histogram (直方图) |
| Median(中位数) | Quartile(四分位数) | Box Plot(箱型图) |
| Mode (众数) | IQR四分位距 | |
| Min | Variance(方差) | |
| Max | Standard Deviation (标准差) | |
| Slewness and Kurtosis (偏度和丰峰度) | ||
| 对于类别型变量,一般使用频次或占比表示每一个变量分布情况,对应的衡量指标分别是类别变量的频次和频率,可以用柱形图来表示可视化分布情况。 |
2. 双变量分析
使用双变量分析可以发现变量之间的关系。根据变量类型的不同,可以分为连续型与连续型、类别型与类别型、类别型与连续型三种双变量分析组合。
(1)连续型与连续型
绘制散点图和计算相关性是分析连续型与连续型双变量的常用方法。
- 绘制散点图:散点图的形状可以反映变量之间的关系是
线性(linear)还是非线性(non-linear)。 - 计算相关性:散点图只能直观的显示双变量(特征)之间的关系,但并不能说明关系的强弱,而相关性可以对变量之间的关系进行量化分析。相关性系数的公式如下:
C o r r e l a t i o n = C o v a r i a n c e ( X , Y ) V a r ( X ) ∗ V a r ( Y ) Correlation = \frac{Covariance(X, Y)}{\sqrt{Var(X) * Var(Y)}} Correlation=Var(X)∗Var(Y)Covariance(X,Y)
相关性系数的取值区间为[-1,1]。当相关性系数为-1时,表示强负线性相关;当相关性系数为1时,表示强正相关;当相关性系数为0时,表示不相关。
一般来说,在取绝对值后,0-0.09为没有相关性,0.1-0.3为弱相关,0.3-0.5为中相关,0.5-0.1为强相关。
(2)类别型与类别型
对于类别型与类别型双变量,一般采用双向表、堆叠柱状图和卡方检验进行分析。
- 双向表:这种方法是通过建立频次(次数)和频率(占比)的双向表来分析变量之间的关系,其中行和列分别表示一个变量。暂时还没找到可以用程序生成的库,但用python画表格是可以的。或者自己用excel做
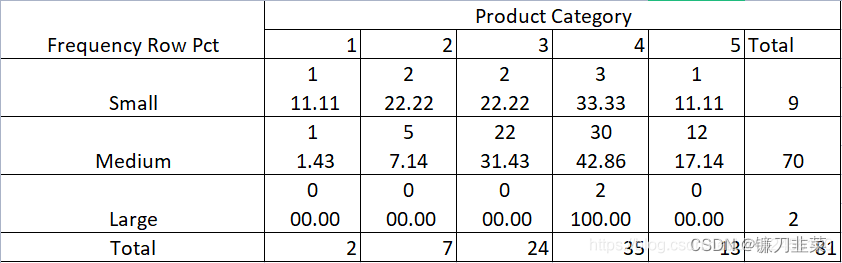 - 堆叠柱状图:这种方法比双向表更加直观
- 堆叠柱状图:这种方法比双向表更加直观
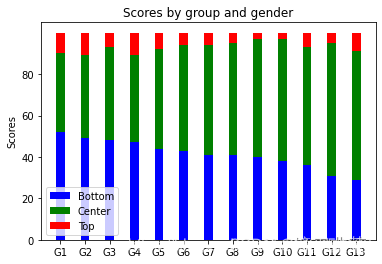
- 卡方检验:主要用于两个和两个以上样本率(构成比)及两个二值型离散变量的关联性分析,即比较理论频次与实际频次的吻合程度或拟合程度。
以iris数据集为例,在sklearn库中使用卡方检验筛选与目标变量相关的特征。
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris = load_iris()
X,y = iris.data,iris.target
ChiValues = chi2(X,y)
X_new = SelectKBest(chi2,k=2).fit_transform(X,y)
X_new
(3)类别型与连续型。在分析类别型和连续型双变量时,可以绘制小提琴图(Violin Plot),这样可以分析类别变量在不同类别时,另一个连续变量的分布情况。
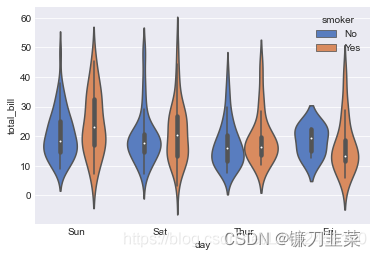
小提琴图结合了箱型图和密度图的相关特征信息,可以直观、清晰地显示数据的分布,常用于展示多组数据的分布及相关的概率密度。
- 分布信息
小提琴图中间的黑色粗条用来显示四分位数。黑色粗条中间的白点表示中位数,粗条的顶边和底边分别表示上四分位数和下四分位数,通过边的位置所对应的y轴的数值就可以看到四分位数的值。
由黑色粗条延伸出的黑细线表示95%的置信区间。 - 概率密度信息
从小提琴图的外形可以看到任意位置的数据密度,实际上就是旋转了90度的密度图。小提琴图越宽,表示密度越大。可以展示出数据的多个峰值。
建议使用Seaborn包中的violinplot()函数
2.1.3 缺失值处理
1. 缺失值的产生原因和分类
缺失值的产生原因多种多样,主要分为机械原因和人为原因。
- 机械原因是由机械导致的数据缺失,比如数据存储的失败,机械故障导致某段时间的数据未能收集(对于定时数据采集而言)。
- 认为原因是由人的主观失误,历史局限或者有意隐瞒造成的数据缺失。
从缺失的分布来看,缺失值主要分为以下四类:
- 完全随机丢失:即对于所有的观察结果,丢失的概率是相同的。
- 随机丢失:即变量的值随机丢失并且丢失的概率会因其他输入变量的值或级别不同而变化。
- 不可预测因子导致的缺失:即数据不是随机缺失,而是受一切潜在因子的影响。
- 取决于自身的缺失:即发生缺失的概率受缺失值本身的影响。
2. 缺失值的处理方法
(1)删除。删除缺失值有两种方法:成列删除(List Wise Deletion)和成对删除(Pair Wise Deletion),两者区别如下:
- 成列删除:某一个样本有一个或多个属性有缺失值则将此样本删除
- 成对删除:删除对应的缺失值,保留更多的样本,不同的变量使用大小不同的样本集
(2)平均值、众数、中值填充。其首先是利用从有效数据集中识别出的关系来评估缺失值,然后用计算的该变量所有已知值得平均值或中值(定量属性)或众数(定性属性)来替换给定属性得缺失值,此方法也是最常用的方法。具体操作为一般填充和相似样本填充。
- 一般填充:是用该变量下所有非缺失值的平均值或中值来补全缺失值。
- 相似样本填充:利用具有相似特征的样本的值或者近似值进行填充。
(3)预测模型填充:即通过建立预测模型来填充缺失值。在这种情况下,会把数据集分为两份:一份是没有缺失值的,用作训练集;另一份是有缺失值的,用作测试集。这样,缺失值的变量就是预测目标,此时可以使用回归、分类等方法来完成填充。
但是这种方法预测出来的值往往更加“规范”,并且,如果变量之间不存在关系,则得到的缺失值会不准确。
2.1.4 异常值处理
通常将远远偏离整个样本总体的观测值称为异常值。
1. 异常值的产生原因和影响
异常值可能是由数据输入误差、测量误差、实验误差、有意造成异常值、数据处理误差、采样误差等因素造成的。
- 数据输入误差:是指在数据收集、输入过程中、人为错误产生的误差。
- 测量误差:这是异常值最常见的来源。
- 实验误差:实验误差也会导致出现异常值。
- 有意造成异常值:这通常发生在一些涉及敏感数据的报告中。
- 数据处理误差:在操作或数据提取的过程中造成的误差。
- 采样误差
异常值对模型和预测分析的影响主要有增加错误方差、降低模型的拟合能力;异常值的非随机分布会降低正态性;与真实值可能存在偏差;影响回归、方差分析等统计模型的基本假设。
2. 异常值的检测
一般可以采用可视化方法进行异常值的检测,常用有箱线图、直方图、散点图。
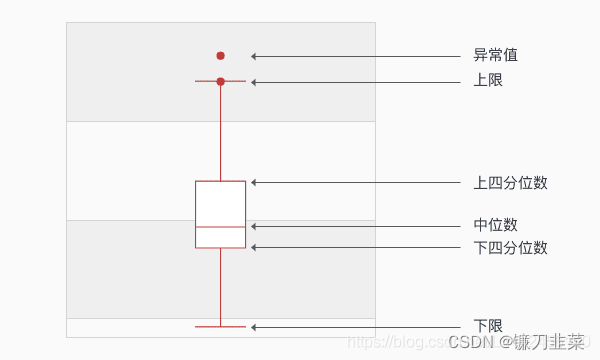
其中IQR(Interquartile Range)四分位距指的是上下四分位数的差值。上限和下限各距离上下四分位数
1.5
∗
I
Q
R
1.5 * IQR
1.5∗IQR。
利用箱线图检测异常值的原则如下:
- 不在 − 1.5 ∗ I Q R -1.5 * IQR −1.5∗IQR和 1.5 ∗ I Q R 1.5 * IQR 1.5∗IQR之间的样本点认为是异常值。
还有两种方法:
- 使用
封顶方法可以认为在第5和第95百分位数范围之外的任何值都是异常值 - 距离
平均值为三倍标准差或者更大的数据点可以被认为是异常值
说明:由于异常值只是对有影响的特殊数据点进行检测,因此它的选择也取决于对业务的理解。
3. 异常值的处理方法
对异常值一般采用删除、转换、填充、区别对待等方法进行处理。
- 删除:如果是由输入误差、数据处理误差引起的异常值,或者异常值很小,则可以直接将其删除。
- 转换:数据转换可以消除异常值,如对数据取对数会减轻由极值引起的变化。
- 填充:使用平均值、中值进行填充,如果异常值是人为造成的,可用预测值填充处理
- 区别对待:如果存在大量的异常值,应在统计模型中区别对待。其中一个方法是将数据分为两个不同的组,异常值归为一组,非异常值归为一组,两组分别建立模型,最终将两组的输出合并。
2.1.5 变量转换
1. 变量转换的目的
在使用直方图、核密度估计等工具对特征分布进行分析时,可能会发现一些变量的取值分布不均匀,这将会极大影响估计。为此,我们需要对变量的取值区间等进行转换,使其分布落在合理的区间内。
2. 变量转换的方法
变量转换的方法主要包括缩放比例或标准化、非线性关系转换成线性、使倾斜分布对称,变量分组等。
| 变量转换方法 | 说明 |
|---|---|
| 缩放比例或标准化 | 数据具有不同的缩放比例,其不会更改变量的分布 |
| 非线性关系转换成线性 | 将非线性变量的关系转换为线性关系更容易理解,其中对数转换是最常用的一种转换方式 |
| 使倾斜分布对称 | 对于向右倾斜的分布,对变量取平方根或立方根或对数;对于向左倾斜的分布,对变量取平方根或立方或指数 |
| 变量分组 | 根据不同的目标把变量按不同类别分组 |
下面是几种常用的转换方法:
(1)对数变换:对变量取对数,可以更改变量的分布形状。其通常应用于向右倾斜的分布,缺点是不能用于含有零或负值的变量。
(2)取平方根或立方根:变量的平方根和立方根对其分布有波形的影响。取平方根可用于包括零的正值,取立方根可用于取值中有负值(包括零)的情况。
(3)变量分组:对变量进行分类,如可以基于原始值、百分比或频率等对变量分类。例如,我们可以将收入分为高、中、低三类。其可以应用于连续型数据,超高维逻辑回归就是采用这种方式产生one-hot变量特征的。
2.1.6 新变量生成
1. 变量生成的目的
变量生成是基于现有变量生成新变量的过程。生成的新变量可能与目标变量有更好的相关性,有助于进行数据分析。例如,可以将日期20xx-xx-xx变量拆分成年、月、日,也可能会发现与目标变量相关性更强的新变量。
2. 变量生成的方法
有两种生成新变量的方法:
(1)创建派生变量:指使用一组函数或不同方法从现有变量创建新变量。例如,在某个数据集中需要预测缺失的年龄值,为了预测缺失项的价值,我们可以提取名称中的称呼(Master、Mr、Mrs、Miss)作为新变量。
(2)创建哑变量:将类别型变量转换为数值型变量。例如将性别变量转换为男性和女性,1为是,0为否。
2.2 数据探索
2.2.1 导入工具包
先导入一些常用的数据处理和可视化的包:numpy、pandas、matplotlib等;另外Seaborn是在matplotlib的基础上进行了更高级的API封装,从而使得作图更加容易,在大多数情况下使用seaborn能做出很具有吸引力的图,而使用matplotlib就能制作具有更多特色的图。应该把Seaborn视为matplotlib的补充,而不是替代物。同时它能高度兼容numpy与pandas数据结构以及scipy与statsmodels等统计模式。
Scipy是一个用于数学、科学、工程领域的常用软件包,可以处理插值、积分、优化、图像处理、常微分方程数值解的求解、信号处理等问题。它用于有效计算Numpy矩阵,使Numpy和Scipy协同工作,高效解决问题。
Scipy是由针对特定任务的子模块组成:
| 模块名 | 应用领域 |
|---|---|
| scipy.cluster | 向量计算/Kmeans |
| scipy.constants | 物理和数学常量 |
| scipy.fftpack | 傅立叶变换 |
| scipy.integrate | 积分程序 |
| scipy.interpolate | 插值 |
| scipy.io | 数据输入输出 |
| scipy.linalg | 线性代数程序 |
| scipy.ndimage | n维图像包 |
| scipy.odr | 正交距离回归 |
| scipy.optimize | 优化 |
| scipy.signal | 信号处理 |
| scipy.sparse | 稀疏矩阵 |
| scipy.spatial | 空间数据结构和算法 |
| scipy.special | 一些特殊的数学函数 |
| scipy.stats | 统计 |
warnings.filterwarnings(“ignore”)可以帮助过滤掉一些不必要的异常.
%matplotlib inline 是一个魔法函数,加上之后不用plt.show()也可以显示图像
## 导入工具包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#%%
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
2.2.2 读取数据
使用Pandas的read_csv()函数进行数据读取,由于读取的是文本文件(.txt),因此需要设置分隔符’\t’。
train_data_file='../data/zhengqi_train.txt'
test_data_file='../data/zhengqi_test.txt'
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
2.2.3 查看数据
首先,使用data.info()函数查看数据集的基本信息。
# 查看数据
train_data.info()
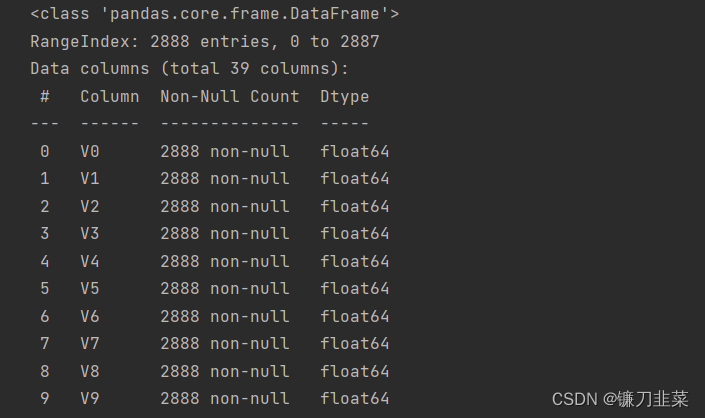
发现:①训练数据集中有2888个样本,数据中有V0~V37共38个特征变量,变量类型都为数值型,所有数据特征没有缺失值。②数据字段采用了脱敏处理,删除了特征数据的具体含义。③target字段为标签变量。
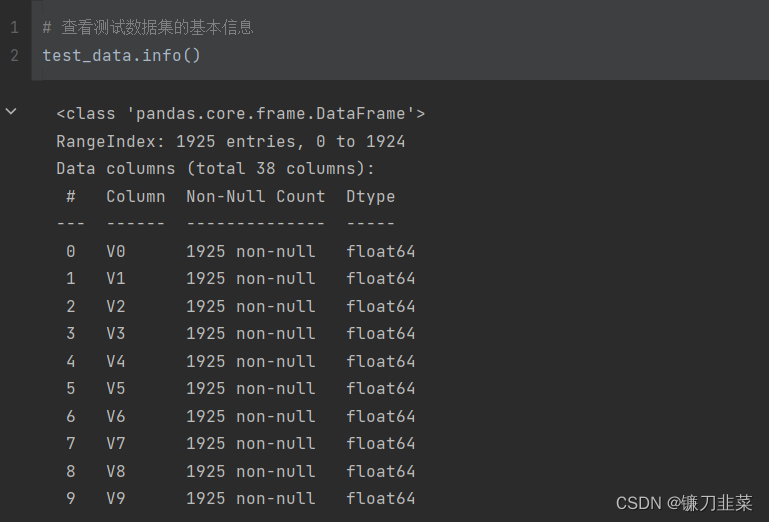
①测试数据集共有1925个样本,特征数目和结构基本与训练数据集相同。②测试集中没有target字段(标签变量),这是需要进行预测的。
然后,查看训练集和测试集的统计信息:
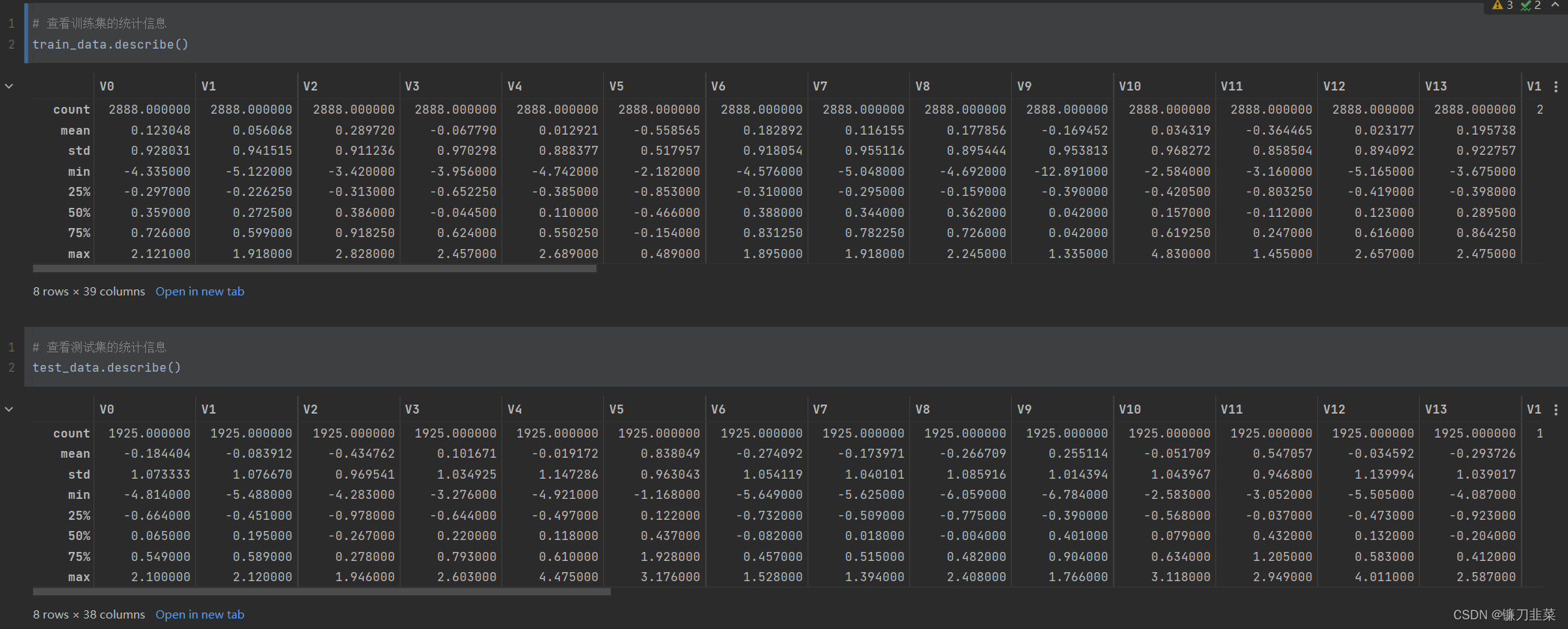
上面的结果中显示了数据的统计信息,如样本数、数据的均值(mean)、标准差(std)、最小值、最大值等。
之后,查看训练集和测试集的字段信息:
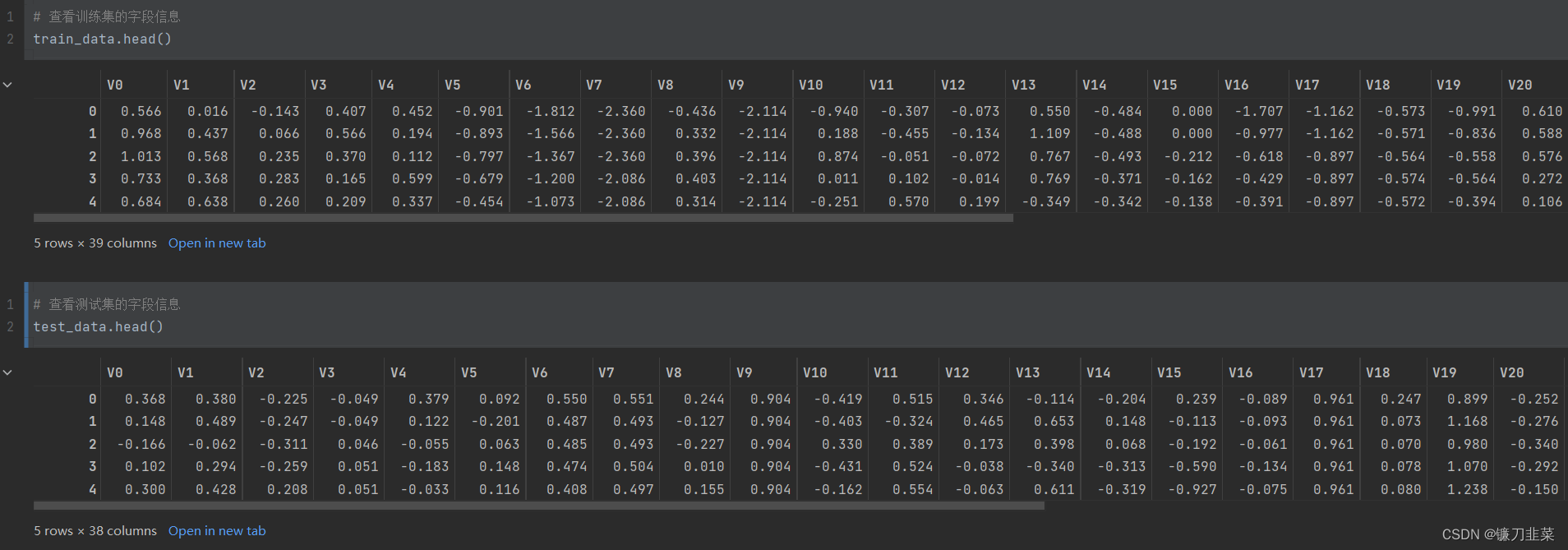
使用data.head()查看了前5条数据,可以看到数据都是浮点型,变量为数值型和连续型。
2.2.4 可视化数据分布
这里主要用seaborn和matplotlib搭配使用来做数据可视化。
- 箱型图
这里画出了38个特征变量V0~V37的箱形图,上面异常值处理的箱线图是竖立摆放,这里是横放,但原理一致:
columns = train_data.columns.tolist()[:39] # 列表头
fig = plt.figure(figsize=(80,60), dpi=75)
for i in range(38):
plt.subplot(7,8,i+1) #7行8列的第i个子图
sns.boxplot(train_data[columns[i]], orient="h", width=0.5) # 箱式图
plt.ylabel(columns[i], fontsize=36)

从图中发现数据存在许多偏离较大的异常,可以考虑移除。
- 获取异常数据并画图
此方法是采用模型预测的形式找出异常值,在完成模型训练和验证的理论讲解后,再介绍此部分
获取异常数据的函数:
from sklearn.metrics import mean_squared_error
# 获取异常数据的函数
def fine_outliers(model, X, y, sigma=3):
# predict y values using model
try:
y_pred = pd.Series(model.predict(X), index=y.index)
# if predicting fails, try fitting the model first
except:
model.fit(X, y)
y_pred = pd.Series(model.predict(X), index=y.index)
# calculate residuals between the model prediction and true y values
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
# calculate z statistic, define outliers to be where |z|>sigma
z = (resid - mean_resid) / std_resid
outliers = z[abs(z) > sigma].index
# print and plot the results
print('R2=', model.score(X, y))
print('mse=', mean_squared_error(y, y_pred))
print('------------------------------------------------')
print('mean of residuals:', mean_resid)
print('std of residuals:', std_resid)
print('------------------------------------------------')
print(len(outliers), 'outliers:')
print(outliers.tolist())
plt.figure(figsize=(15, 5))
ax_131 = plt.subplot(1, 3, 1)
plt.plot(y, y_pred, '.')
plt.plot(y.loc[outliers], y_pred.loc[outliers], 'ro')
plt.legend(['Accepted', 'Outlier'])
plt.xlabel('y')
plt.ylabel('y_pred');
ax_132 = plt.subplot(1, 3, 2)
plt.plot(y, y - y_pred, '.')
plt.plot(y.loc[outliers], y.loc[outliers] - y_pred.loc[outliers], 'ro')
plt.legend(['Accepted', 'Outliers'])
plt.xlabel('y')
plt.ylabel('y-y_pred');
ax_133 = plt.subplot(1, 3, 3)
z.plot.hist(bins=50, ax=ax_133)
z.loc[outliers].plot.hist(color='r', bins=50, ax=ax_133)
plt.legend(['Accepted', 'Outlier'])
plt.xlabel('z')
plt.savefig('../output/outliers.png')
return outliers
这里通过岭回归模型找出异常值,并绘制其分布,代码如下:
from sklearn.linear_model import Ridge
X_train = train_data.iloc[:,0:-1]
y_train = train_data.iloc[:,-1]
outliers = fine_outliers(Ridge(), X_train, y_train)
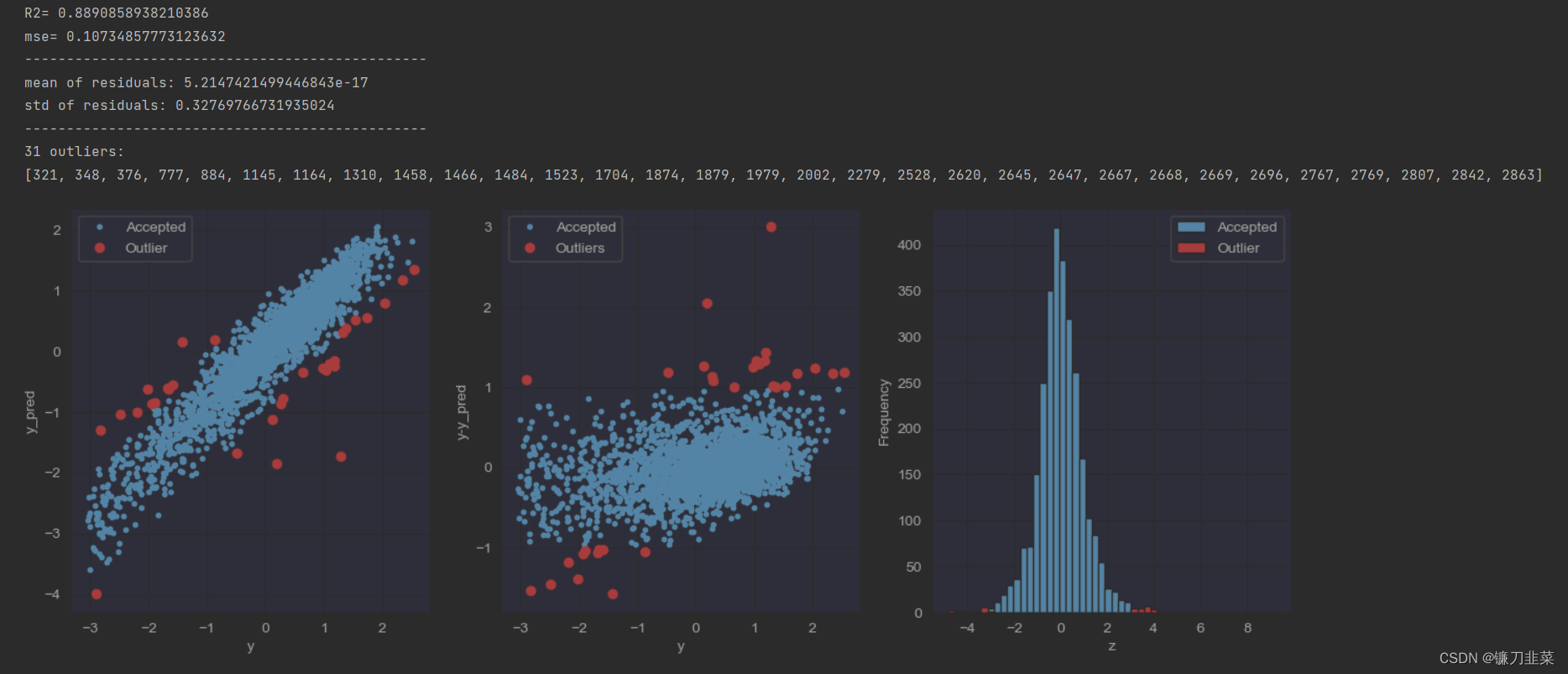
- 直方图和Q-Q图
Q-Q图是指数据的分位数和正态分布的分位数对比参照的图,如果数据符合正态分布,则所有的点都会落在直线上。
首先,通过绘制特征变量V0的直方图查看其在训练集中的统计分布,并绘制Q-Q图查看V0的分布是否近似于正态分布。
from scipy import stats
plt.figure(figsize=(10, 5))
ax = plt.subplot(1, 2, 1)
sns.distplot(train_data.V0, fit=stats.norm)
ax = plt.subplot(1, 2, 2)
res = stats.probplot(train_data.V0, plot=plt)
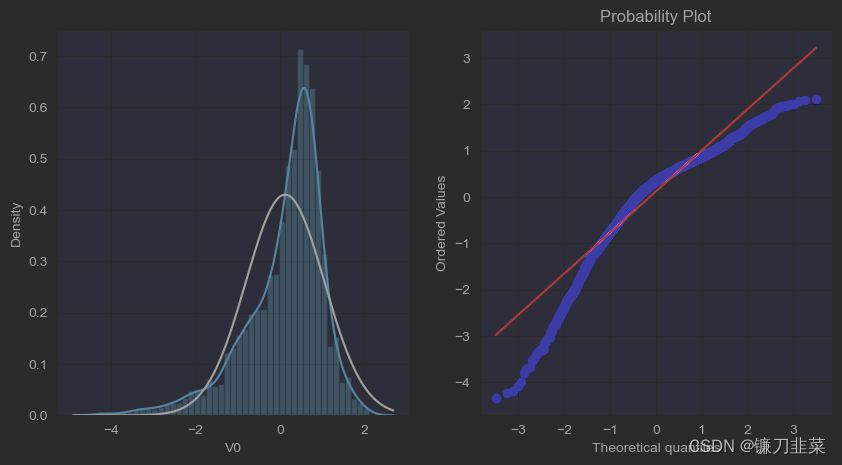
可以看到,训练数据集中特征变量V0的分布不是正态分布。
然后,绘制训练数据集中所有变量的直方图和Q-Q图.
train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4 * train_cols, 4 * train_rows))
i = 0
for col in train_data.columns:
i += 1
ax = plt.subplot(train_rows, train_cols, i)
sns.distplot(train_data[col], fit=stats.norm)
i += 1
ax = plt.subplot(train_rows, train_cols, i)
res = stats.probplot(train_data[col], plot=plt)
plt.tight_layout()
plt.show()
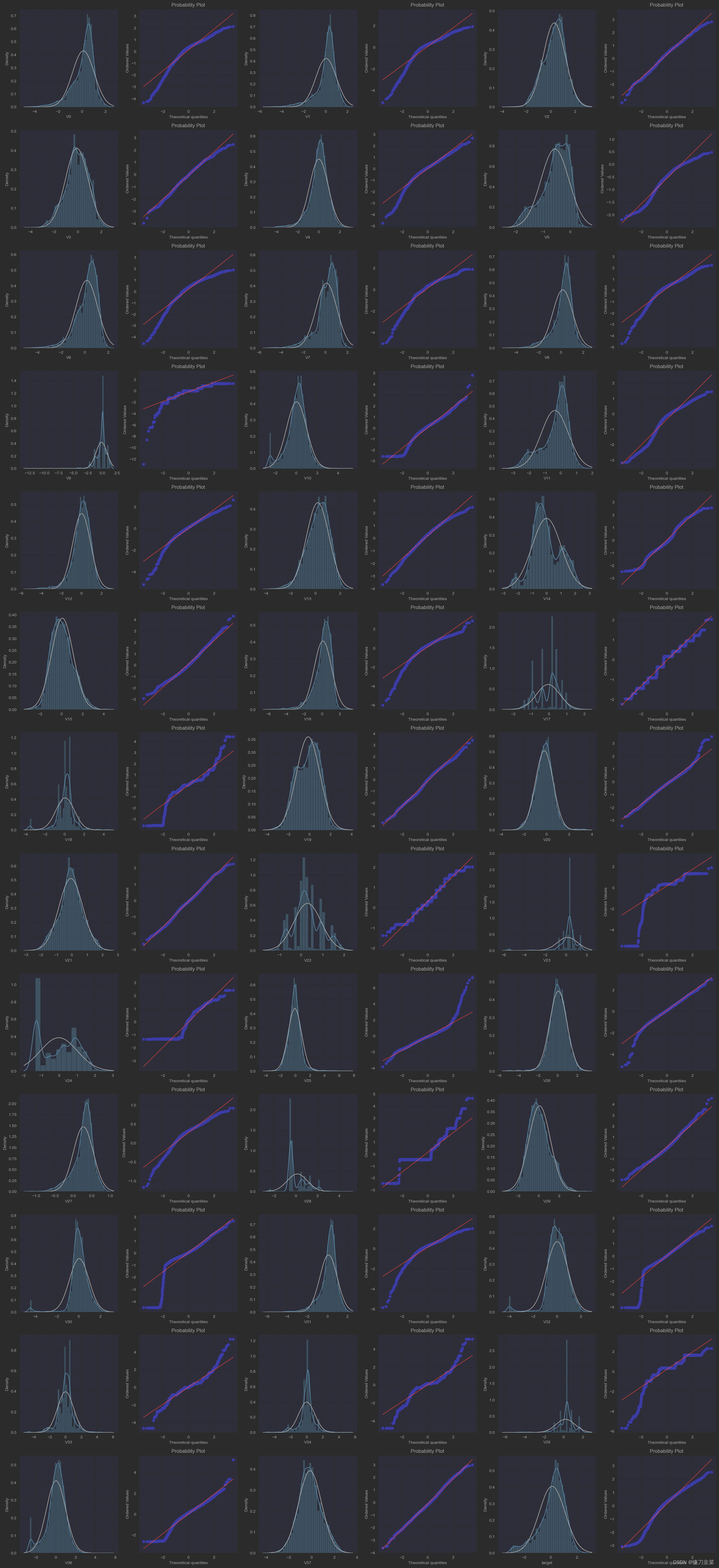
从数据分布图中可以发现,很多特征变量(例如V1,V9,V24,V28等)的数据分布不是正态的,数据并不跟随对角线分布,后续可以使用数据变量对其进行处理。
- KDF分布图
KDE(Kernel Density Estimation,核密度估计)可以理解为对直方图的加窗平滑。通过绘制KDE分布图,可以查看并对比训练集和测试集中特征变量的分布情况,发现两个数据集中分布不一致的特征变量。
首先对比同一特征变量V0在训练集和测试集中的分布情况,并查看数据分布是否一致。
plt.figure(figsize=(8, 4), dpi=150)
ax = sns.kdeplot(train_data['V0'], color='Red', shade=True)
ax = sns.kdeplot(test_data['V0'], color='Blue', shade=True)
ax.set_xlabel('V0')
ax.set_ylabel('Frequency')
ax = ax.legend(['train', 'test'])
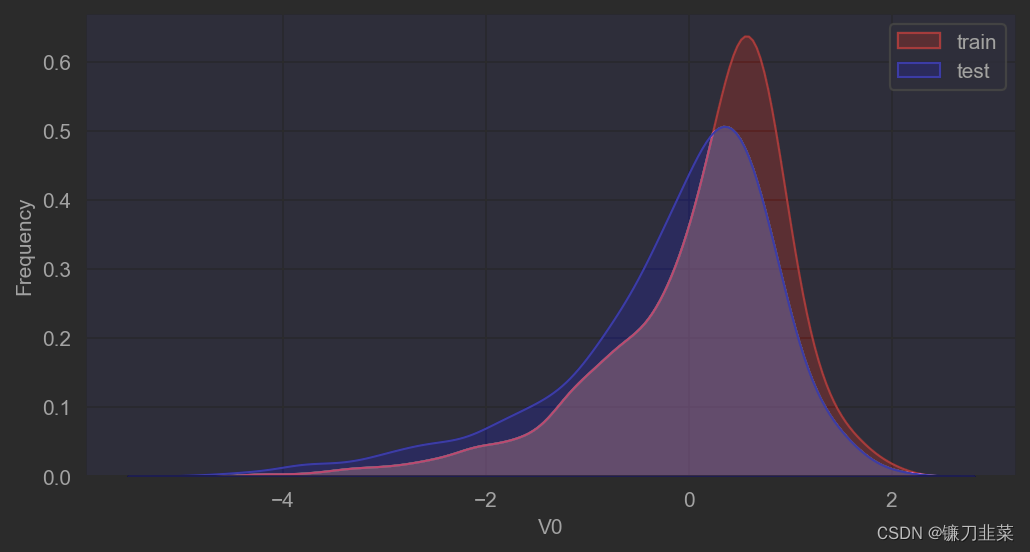
可以看到,V0在两个数据集中的分布基本一致。
然后,对比所有变量在训练集和测试集中的KDE分布:
dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4 * dist_cols, 4 * dist_rows))
i=1
for col in test_data.columns:
ax = plt.subplot(dist_rows, dist_cols, i)
ax = sns.kdeplot(train_data[col], color='Red', shade=True)
ax = sns.kdeplot(test_data[col], color='Blue', shade=True)
ax.set_xlabel(col)
ax.set_ylabel('Frequency')
ax = ax.legend(['train', 'test'])
i += 1
plt.show()

从图中发现,特征变量V5,V9,V11,V17,V22,V28在训练集和测试集中的分布不一致,这会导致模型的泛化能力变差,需要删除此类特征。
- 线性回归图
线性回归关系图主要用于分析变量之间的线性回归关系。首先查看特征变量V0与target变量的线性回归关系。
fcols = 2
frows = 1
plt.figure(figsize=(8, 4), dpi=150)
ax = plt.subplot(1, 2, 1)
sns.regplot(x='V0', y='target', data=train_data, ax=ax, scatter_kws={'marker':'.','s':3,'alpha':0.3}, line_kws={'color':'k'});
plt.xlabel('V0')
plt.ylabel('target')
ax = plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')
plt.show()
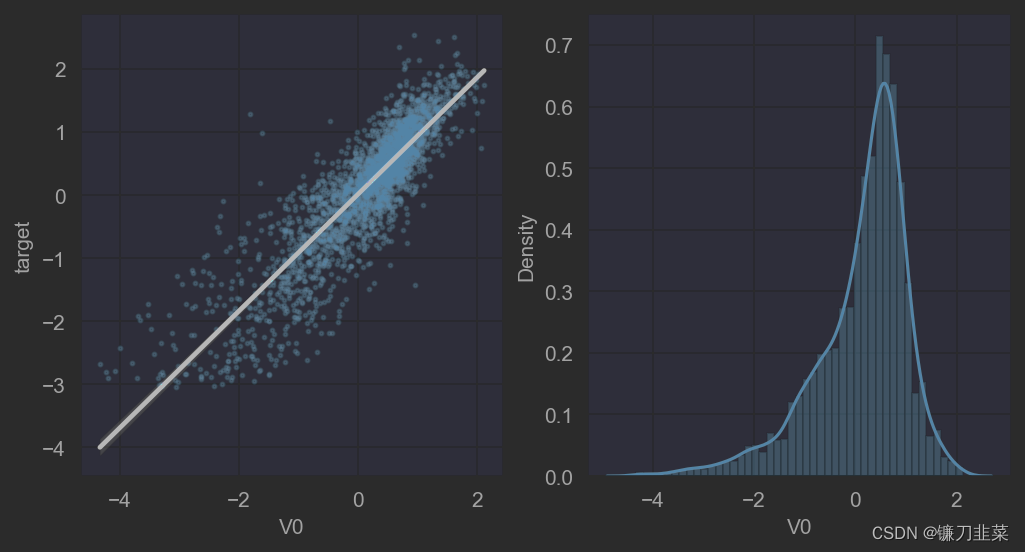
然后,查看所有特征变量与target变量的线性回归关系。
plt.show()
#%%
fcols=6
frows=len(test_data.columns)
plt.figure(figsize=(5*fcols, 4*frows))
i=0
for col in test_data.columns:
i+=1
ax = plt.subplot(frows, fcols, i)
sns.regplot(x=col, y='target', data=train_data, ax=ax, scatter_kws={'marker':'.','s':3,'alpha':0.3}, line_kws={'color':'k'});
plt.xlabel(col)
plt.ylabel('target')
i+=1
ax = plt.subplot(frows, fcols, i)
sns.distplot(train_data[col].dropna())
plt.xlabel(col)

2.2.5 查看特征变量的相关性
对特征变量的相关性进行分析,可以发现特征变量和目标变量及特征变量之间的关系,为在特征工程中提取特征做准备。
- 计算相关性系数
在删除训练集和测试集中分布不一致的变量后,计算剩余变量与target之间的相关性系数。
pd.set_option('display.max_columns', 10)
pd.set_option('display.max_rows', 10)
data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28'], axis=1)
train_corr = data_train1.corr()
train_corr

- 画出相关性热力图
为了便于分析,将相关系数的结果以热力图的形式显示
ax = plt.subplots(figsize=(20, 16)) # 调整画布大小
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True) #画热力图 annot=True 显示系数

结果中可以看出各个特征变量(V0~V37)之间的相关性以及它们与target变量的相关性。
- 根据相关系数筛选特征变量
首先寻找K个与target变量最相关的特征变量(K=10):
k = 10 # number of variables for heatmap
cols = train_corr.nlargest(k, 'target')['target'].index
cm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10, 10)) # 调整画布大小
hm = sns.heatmap(train_data[cols].corr(), annot=True, square=True)
plt.show()
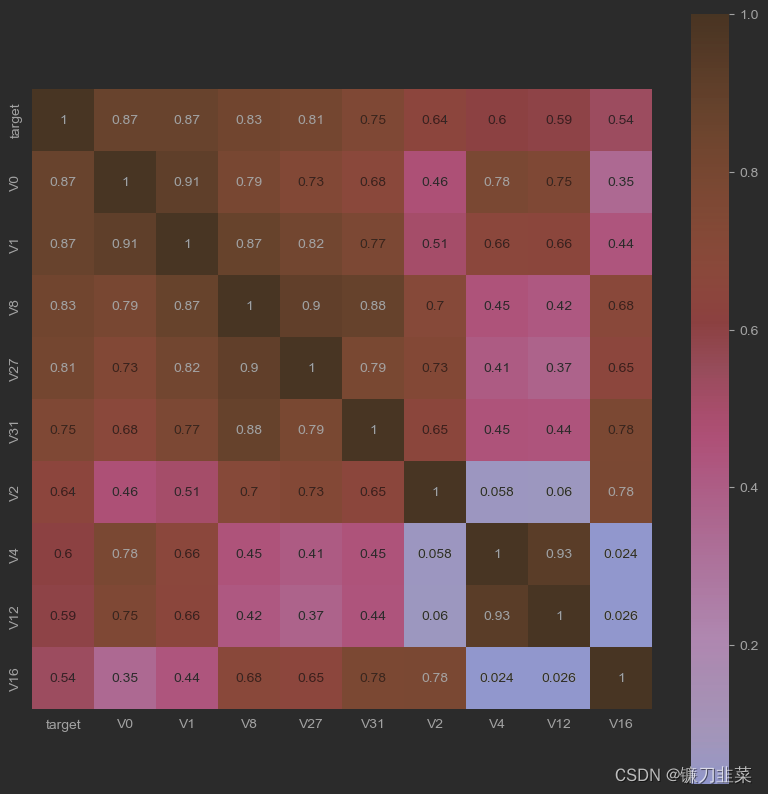
然后,找出与target变量的相关系数大于0.5的特征变量
threshold = 0.5
corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat["target"]) > threshold]
plt.figure(figsize=(10, 10))
g = sns.heatmap(train_data[top_corr_features].corr(), annot=True, cmap="RdYlGn")
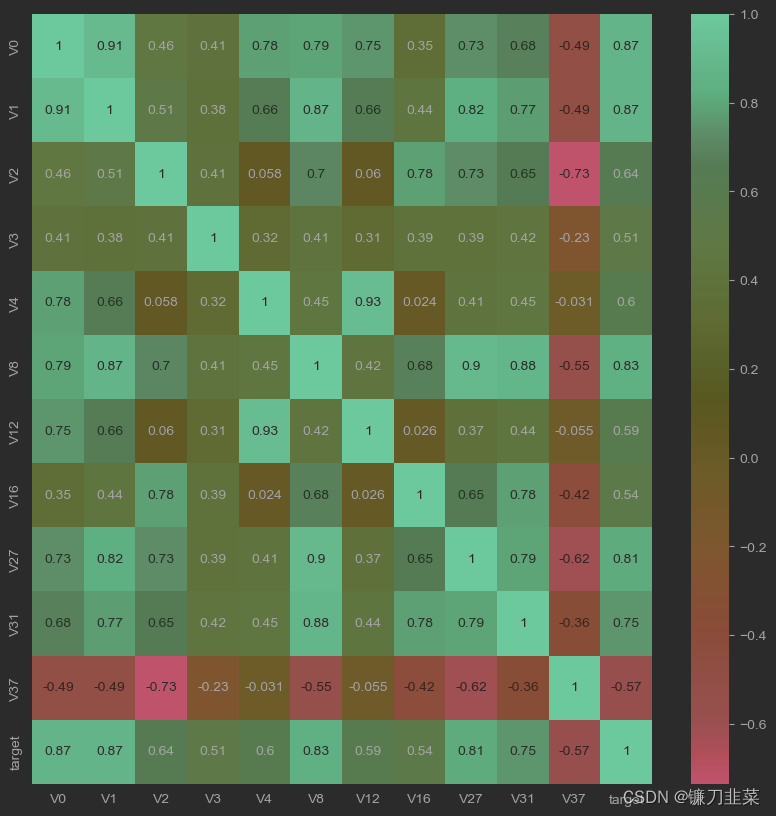
可以发现,与target变量的相关系数大于0.5的特征变量都被直观地筛选出来。该方法可以简单直观地判断哪些特征变量线性相关,相关系数越大,就认为这些变量对target变量的线性影响越大。
说明:相关性选择主要用于判别线性相关,对于target变量如果存在更复杂的函数形式的影响,则建议使用树模型的特征重要性去选择。
用相关系数阈值移除相关特征:
threshold = 0.5
# Absolute value correlation matrix
corr_matrix = data_train1.corr().abs()
drop_col = corr_matrix[corr_matrix["target"] < threshold].index
#data_all.drop(drop_col, axis=1, inplace=True) # 这里暂不删除,后续分析还会用到
- Box-Cox变换
由于线性回归是基于正态分布的,因此在进行统计分析时,需要将数据转换使其符合正态分布。
Box-Cox变换是统计建模中常用的一种数据转换方法。在连续的响应变量不满足正态分布时,可以使用Box-Cox变换,这一变换可以使线性回归模型在满足线性、正态性、独立性以及方差齐性的同时,又不丢失信息。在对数据做Box-Cox变换之后,可以在一定程度上减少不可观测的误差和预测变量的相关性,这有利于线性模型的拟合及分析出特征的相关性。
在做Box-Cox变换之前,需要对数据做归一化预处理。在归一化时,对数据进行合并操作可以使训练数据和测试数据一致。这种方式可以在线下分析建模中使用,而线上部署只需采用训练数据的归一化即可。
drop_columns = ['V5','V9','V11','V17','V22','V28']
# 合并训练集和测试集的数据
train_x = train_data.drop(['target'], axis=1)
#data_all=pd.concat([train_data,test_data],axis=0,ignore_index=True)
data_all = pd.concat([train_x,test_data])
data_all.drop(drop_columns, axis=1, inplace=True)
data_all.head()
对合并后的每列数据进行归一化:
cols_numeric = list(data_all.columns)
def scale_minmax(col):
return (col - col.min()) / (col.max() - col.min())
data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax, axis=0)
data_all[cols_numeric].describe()
也可以分开对训练数据和测试数据进行归一化处理,不过这种方式需要建立在训练数据和测试数据分布一致的前提下,建议在数据量大的情况下使用(数据量大,一般分布比较一致),能加快归一化的速度。而数据量较小会存在分布差异较大的情况,此时,在数据分析和线下建模中应该将数据统一归一化。
train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_minmax, axis=0)
test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_minmax, axis=0)
对特征变量做Box-Cox变换后,计算分位数并画图展示(基于正态分布),显示特征变量与target变量的线性关系。代码如下:
# 这里是将特征分为两部分,前13个为第一部分
cols_numeric_left = cols_numeric[0:13]
cols_numeric_right = cols_numeric[13:]
## Check effect of Box-Cox transforms on distributions of continuous variables
train_data_process = pd.concat([train_data_process, train_data['target']], axis=1)
fcols = 6
frows = len(cols_numeric_left)
plt.figure(figsize=(4 * fcols, 4 * frows))
i = 0
for var in cols_numeric_left:
dat = train_data_process[[var, 'target']].dropna()
i += 1
plt.subplot(frows, fcols, i)
sns.distplot(dat[var], fit=stats.norm);
plt.title(var + ' Original')
plt.xlabel('')
i += 1
plt.subplot(frows, fcols, i)
_ = stats.probplot(dat[var], plot=plt)
plt.title('skew=' + '{:.4f}'.format(stats.skew(dat[var]))) #计算数据集的偏度
plt.xlabel('')
plt.ylabel('')
i += 1
plt.subplot(frows, fcols, i)
plt.plot(dat[var], dat['target'], '.', alpha=0.5)
plt.title('corr=' + '{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))
i += 1
plt.subplot(frows, fcols, i)
trans_var, lambda_var = stats.boxcox(dat[var].dropna() + 1)
trans_var = scale_minmax(trans_var) # 数据归一化
sns.distplot(trans_var, fit=stats.norm);
plt.title(var + ' Transformed')
plt.xlabel('')
i += 1
plt.subplot(frows, fcols, i)
_ = stats.probplot(trans_var, plot=plt)
plt.title('skew=' + '{:.4f}'.format(stats.skew(trans_var))) #归一化后,偏度明显变小,相关性变化不大
plt.xlabel('')
plt.ylabel('')
i += 1
plt.subplot(frows, fcols, i)
plt.plot(trans_var, dat['target'], '.', alpha=0.5)
plt.title('corr=' + '{:.2f}'.format(np.corrcoef(trans_var, dat['target'])[0][1]))

可以发现,经过变换后,变量分布更接近正态分布,而且从图中可以更加直观地看出特征变量与target变量的线性相关性。
参考资料
- 《阿里云天池大赛赛题解析——机器学习篇》
- Python机器学习及分析工具:Scipy篇
- 数据归一化 minmax_scale()函数解析








 本文解析了工业蒸汽量预测赛题,介绍了火力发电的基本原理、赛题目标、数据概览等内容,探讨了回归预测模型的选择及数据探索过程。
本文解析了工业蒸汽量预测赛题,介绍了火力发电的基本原理、赛题目标、数据概览等内容,探讨了回归预测模型的选择及数据探索过程。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










